
2019版高中数学二轮复习教师用书:专题七 解析几何
展开专题七 解析几何
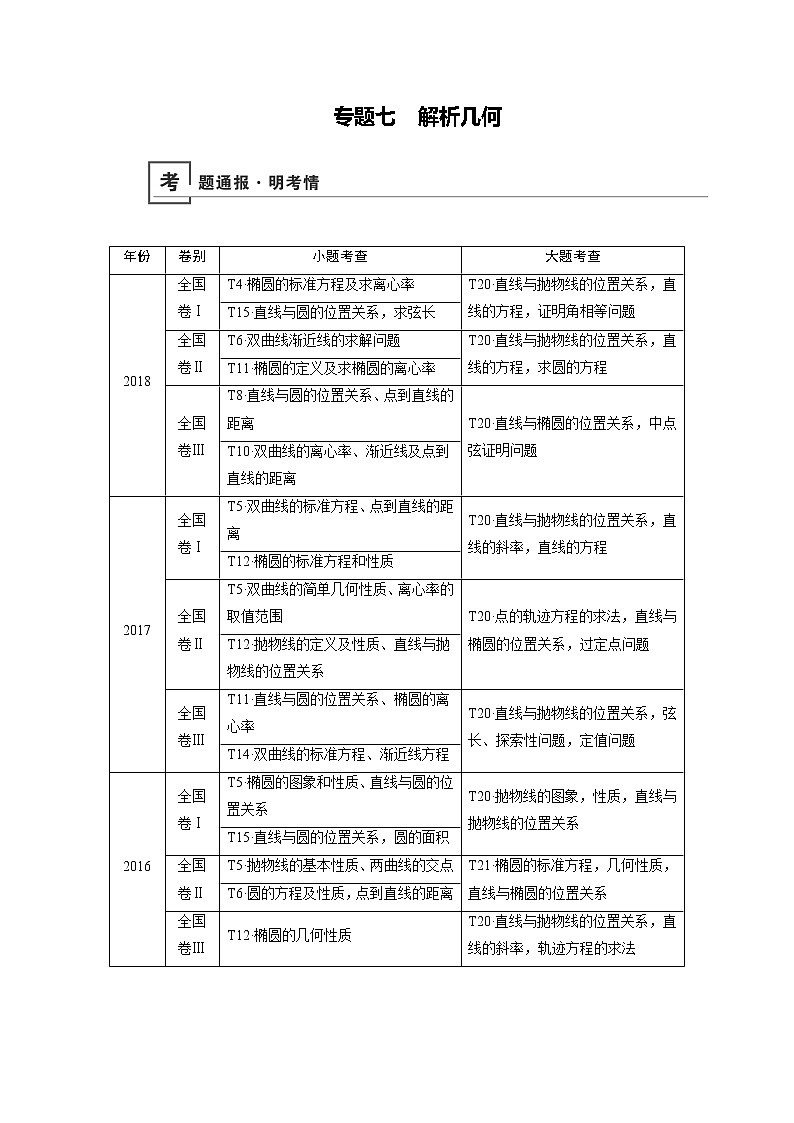
年份 | 卷别 | 小题考查 | 大题考查 |
2018 | 全国卷Ⅰ | T4·椭圆的标准方程及求离心率 | T20·直线与抛物线的位置关系,直线的方程,证明角相等问题 |
T15·直线与圆的位置关系,求弦长 | |||
全国卷Ⅱ | T6·双曲线渐近线的求解问题 | T20·直线与抛物线的位置关系,直线的方程,求圆的方程 | |
T11·椭圆的定义及求椭圆的离心率 | |||
全国卷Ⅲ | T8·直线与圆的位置关系、点到直线的距离 | T20·直线与椭圆的位置关系,中点弦证明问题 | |
T10·双曲线的离心率、渐近线及点到直线的距离 | |||
2017 | 全国卷Ⅰ | T5·双曲线的标准方程、点到直线的距离 | T20·直线与抛物线的位置关系,直线的斜率,直线的方程 |
T12·椭圆的标准方程和性质 | |||
全国卷Ⅱ | T5·双曲线的简单几何性质、离心率的取值范围 | T20·点的轨迹方程的求法,直线与椭圆的位置关系,过定点问题 | |
T12·抛物线的定义及性质、直线与抛物线的位置关系 | |||
全国卷Ⅲ | T11·直线与圆的位置关系、椭圆的离心率 | T20·直线与抛物线的位置关系,弦长、探索性问题,定值问题 | |
T14·双曲线的标准方程、渐近线方程 | |||
2016 | 全国卷Ⅰ | T5·椭圆的图象和性质、直线与圆的位置关系 | T20·抛物线的图象,性质,直线与抛物线的位置关系 |
T15·直线与圆的位置关系,圆的面积 | |||
全国卷Ⅱ | T5·抛物线的基本性质、两曲线的交点 | T21·椭圆的标准方程,几何性质,直线与椭圆的位置关系 | |
T6·圆的方程及性质,点到直线的距离 | |||
全国卷Ⅲ | T12·椭圆的几何性质 | T20·直线与抛物线的位置关系,直线的斜率,轨迹方程的求法 |
解析几何问题重在“设”——设点、设线
解析几何部分知识点多,运算量大,能力要求高,综合性强,在高考试题中大都是在压轴题的位置出现,是考生“未考先怕”的题型之一,不是怕解题无思路,而是怕解题过程中繁杂的运算.因此,在遵循“设——列——解”程序化运算的基础上,应突出解析几何“设”的重要性,以克服平时重思路方法、轻运算技巧的顽疾,突破如何避繁就简这一瓶颈.
【典例】 已知抛物线C:y2=2x的焦点为F,平行于x轴的两条直线l1,l2分别交C于A,B两点,交C的准线于P,Q两点.
(1)若F在线段AB上,R是PQ的中点,证明AR∥FQ;
(2)若△PQF的面积是△ABF的面积的两倍,求AB中点的轨迹方程.
[解题示范] 由题设F.
设l1:y=a,l2:y=b,则ab≠0❶,
且A,B,P,Q,R.
记过A,B两点的直线为l,
则l的方程为2x-(a+b)y+ab=0.
(1)证明:由于F在线段AB上,故1+ab=0.
设AR的斜率为k1,FQ的斜率为k2,则
k1=====-b==k2.
所以AR∥FQ.
(2)解:设l与x轴的交点为D(x1,0)❷,
则S△ABF=|b-a||FD|=|b-a||x1-|,
S△PQF=.
由题设可得2×|b-a||x1-|=,
所以x1=0(舍去),x1=1.
设满足条件的AB的中点为E(x,y)❸.
当AB与x轴不垂直时,
由kAB=kDE可得=(x≠1).
而=y,所以y2=x-1(x≠1).
当AB与x轴垂直时,E与D重合,此时E(1,0)满足方程y2=x-1.
所以所求轨迹方程为y2=x-1.
❶设线:设出直线l1,l2可表示出点A,B,P,Q,R的坐标,进而可表示过A,B两点的直线方程
❷设点:设出直线l与x轴交点,可表示出|DF|,进而表示出S△ABF,根据面积关系,可求得此点坐标
❸设点:要求此点的轨迹方程,先设出此点,根据题目条件得出此点坐标的关系式,即轨迹方程
解决解析几何问题的关键在于:通观全局,局部入手,整体思维,反映在解题上,就是把曲线的几何特征准确地转换为代数形式,根据方程画出图形,研究几何性质.








