

2019版二轮复习数学(理·重点生)通用版讲义:第一部分专题十五统计、统计案例
展开专题十五 统计、统计案例
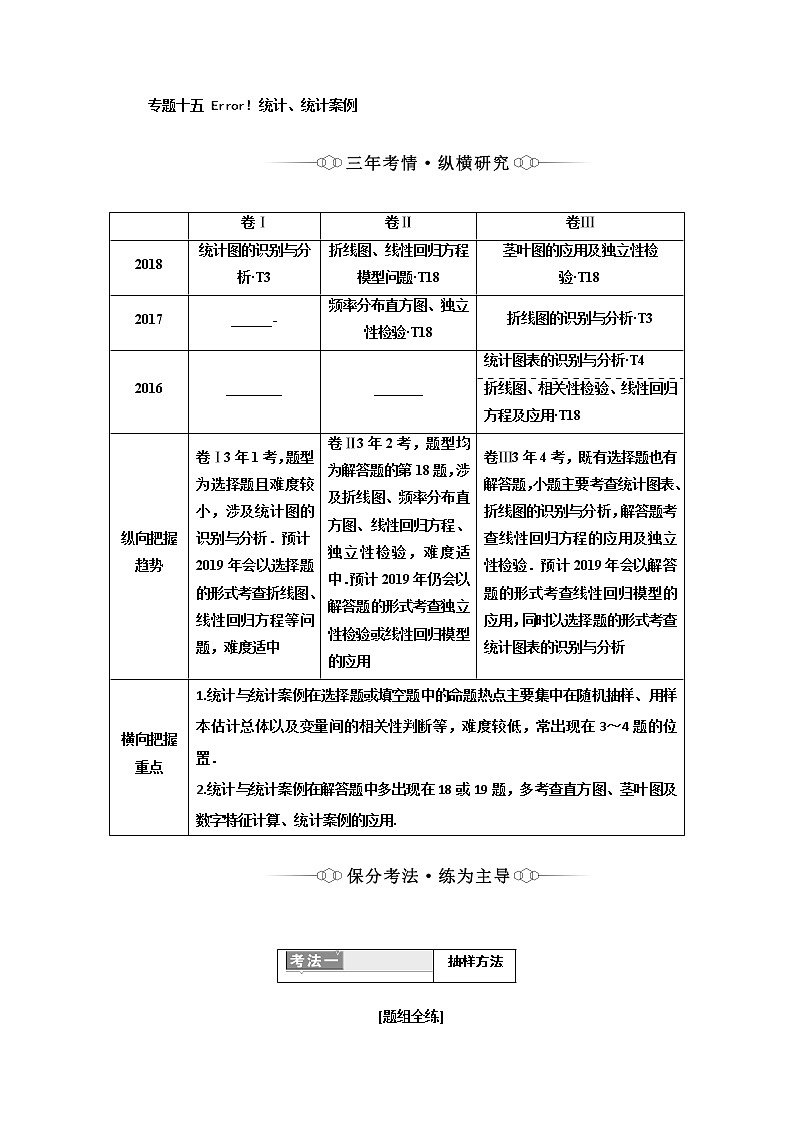
| 卷Ⅰ | 卷Ⅱ | 卷Ⅲ |
2018 | 统计图的识别与分析·T3 | 折线图、线性回归方程模型问题·T18 | 茎叶图的应用及独立性检验·T18 |
2017 | ______- | 频率分布直方图、独立性检验·T18 | 折线图的识别与分析·T3 |
2016 | ________ | _______ | 统计图表的识别与分析·T4 |
折线图、相关性检验、线性回归方程及应用·T18 | |||
纵向把握趋势 | 卷Ⅰ3年1考,题型为选择题且难度较小,涉及统计图的识别与分析.预计2019年会以选择题的形式考查折线图、线性回归方程等问题,难度适中 | 卷Ⅱ3年2考,题型均为解答题的第18题,涉及折线图、频率分布直方图、线性回归方程、独立性检验,难度适中.预计2019年仍会以解答题的形式考查独立性检验或线性回归模型的应用 | 卷Ⅲ3年4考,既有选择题也有解答题,小题主要考查统计图表、折线图的识别与分析,解答题考查线性回归方程的应用及独立性检验.预计2019年会以解答题的形式考查线性回归模型的应用,同时以选择题的形式考查统计图表的识别与分析 |
横向把握重点 | 1.统计与统计案例在选择题或填空题中的命题热点主要集中在随机抽样、用样本估计总体以及变量间的相关性判断等,难度较低,常出现在3~4题的位置. 2.统计与统计案例在解答题中多出现在18或19题,多考查直方图、茎叶图及数字特征计算、统计案例的应用. | ||
抽样方法 |
[题组全练]
1.(2018·石家庄模拟)某校高一年级有男生560人,女生420人,用分层抽样的方法从该年级全体学生中抽取一个容量为140的样本,则此样本中男生人数为( )
A.80 B.120
C.160 D.240
解析:选A 因为男生和女生的比例为560∶420=4∶3,样本容量为140,所以应该抽取男生的人数为140×=80,故选A.
2.(2018·南宁模拟)已知某地区中小学生人数和近视情况分别如图甲和图乙所示.为了了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为( )
A.100,20 B.200,20
C.200,10 D.100,10
解析:选B 由题图甲可知学生总人数是10 000,样本容量为10 000×2%=200,抽取的高中生人数是2 000×2%=40,由题图乙可知高中生的近视率为50%,所以高中生的近视人数为40×50%=20,故选 B.
3.从30个个体(编号为00~29)中抽取10个样本,现给出某随机数表的第11行到第15行(见下表),如果某人选取第12行的第6列和第7列中的数作为第一个数并且由此数向右读,则选取的前4个的号码分别为( )
9264 4607 2021 3920 7766 3817 3256 1640
5858 7766 3170 0500 2593 0545 5370 7814
2889 6628 6757 8231 1589 0062 0047 3815
5131 8186 3709 4521 6665 5325 5383 2702
9055 7196 2172 3207 1114 1384 4359 4488
A.76,63,17,00 B.16,00,02,30
C.17,00,02,25 D.17,00,02,07
解析:选D 在随机数表中,将处于00~29的号码选出,满足要求的前4个号码为17,00,02,07.
4.(2019届高三·南昌调研)某校高三(2)班现有64名学生,随机编号为0,1,2,…,63,依编号顺序平均分成8组,组号依次为1,2,3,…,8.现用系统抽样方法抽取一个容量为8的样本,若在第1组中随机抽取的号码为5,则在第6组中抽取的号码为________.
解析:由题知分组间隔为=8,又第1组中抽取的号码为5,所以第6组中抽取的号码为5×8+5=45.
答案:45
5.采用系统抽样方法从1 000人中抽取50人做问卷调查,将他们随机编号1,2,…,1 000.适当分组后在第一组采用简单随机抽样的方法抽到的号码为8.若抽到的50人中,编号落入区间[1,400]的人做问卷A,编号落入区间[401,750]的人做问卷B,其余的人做问卷C,则抽到的人中,做问卷C的人数为________.
解析:根据系统抽样的特点可知,所有做问卷调查的人的编号构成首项为8,公差d==20的等差数列{an},∴通项公式an=8+20(n-1)=20n-12,令751≤20n-12≤1 000,得≤n≤,又∵n∈N*,∴39≤n≤50,∴做问卷C的共有12人.
答案:12
[系统方法]
解决抽样问题应关注的两点
(1)解决此类题目的关键是深刻理解各种抽样方法的特点和适用范围.但无论哪种抽样方法,每一个个体被抽到的概率都是相等的,都等于样本容量与总体容量的比值.
(2)在系统抽样的过程中,要注意分段间隔,需要抽取n个个体,样本就需要分成n个组,则分段间隔即为(N为样本容量),首先确定在第一组中抽取的个体的号码数,再从后面的每组中按规则抽取每个个体.
用样本估计总体 |
[题组全练]
1.(2019届高三·贵阳模拟)在某中学举行的环保知识竞赛中,将三个年级参赛学生的成绩进行整理后分为5组,绘制如图所示的频率分布直方图,图中从左到右依次为第一、第二、第三、第四、第五小组,已知第二小组的频数是40,则成绩在80~100分的学生人数是( )
A.15 B.18
C.20 D.25
解析:选A 根据频率分布直方图,得第二小组的频率是0.04×10=0.4,∵频数是40,∴样本容量是=100,又成绩在80~100分的频率是(0.01+0.005)×10=0.15,∴成绩在80~100分的学生人数是100×0.15=15.
2.(2018·全国卷Ⅰ)某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图:
则下面结论中不正确的是( )
A.新农村建设后,种植收入减少
B.新农村建设后,其他收入增加了一倍以上
C.新农村建设后,养殖收入增加了一倍
D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
解析:选A 设新农村建设前,农村的经济收入为a,则新农村建设后,农村经济收入为2a.
新农村建设前后,各项收入的对比如下表:
| 新农村建设前 | 新农村建设后 | 新农村建设后变化情况 | 结论 |
种植收入 | 60%a | 37%×2a=74%a | 增加 | A错 |
其他收入 | 4%a | 5%×2a=10%a | 增加一倍以上 | B对 |
养殖收入 | 30%a | 30%×2a=60%a | 增加了一倍 | C对 |
养殖收入+第三产业收入 | (30%+6%)a=36%a | (30%+28%)×2a=116%a | 超过经济收入2a的一半 | D对 |
故选A.
3.(2018·长春质检)已知某班级部分同学一次测验的成绩统计如图,则其中位数和众数分别为( )
A.95,94 B.92,86
C.99,86 D.95,91
解析:选B 由茎叶图可知,此组数据由小到大排列依次为76,79,81,83,86,86,87,91,92,94,95,96,98,99,101,103,114,共17个,故92为中位数,出现次数最多的为众数,故众数为86,故选 B.
4.(2018·武汉调研)从某选手的7个得分中去掉1个最高分,去掉1个最低分后,剩余5个得分的平均数为91分,如图所示是该选手得分的茎叶图,其中有一个数字模糊,无法辨认,在图中用x表示,则剩余5个得分的方差为________.
解析:去掉一个最高分99分,一个最低分87分,剩余的得分为93分,90分,(90+x)分,91分,87分,则=91,解得x=4,所以这5个数的方差s2=[(91-93)2+(91-90)2+(91-94)2+(91-91)2+(91-87)2]=6.
答案:6
[系统方法]
1.频率分布直方图的应用
(1)已知频率分布直方图中的部分数据,求其他数据.可根据频率分布直方图中的数据求出样本与整体的关系,利用频率和等于1就可求出其他数据.
(2)已知频率分布直方图,求某种范围内的数据.可利用图形及某范围结合求解.
2.数字特征及其特点
平均数与方差都是重要的数字特征,是对数据的一种简明描述,它们所反映的情况有着重要的实际意义.平均数、中位数、众数描述数据的集中趋势,方差和标准差描述数据的波动大小.
回归分析 |
[多维例析]
角度一 线性回归分析
(2018·陕西质检)基于移动互联网技术的共享单车被称为“新四大发明”之一,短时间内就风靡全国,带给人们新的出行体验.某共享单车运营公司的市场研究人员为了解公司的经营状况,对该公司2018年6月~11月六个月内的市场占有率进行了统计,结果如下表:
月份 | 6月 | 7月 | 8月 | 9月 | 10月 | 11月 |
月份代码x | 1 | 2 | 3 | 4 | 5 | 6 |
市场占有率y(%) | 11 | 13 | 16 | 15 | 20 | 21 |
(1)请在给出的坐标纸中作出散点图,并用相关系数说明能否用线性回归模型拟合市场占有率y与月份代码x之间的关系;
(2)求y关于x的线性回归方程,并预测该公司2019年3月份的市场占有率.
参考数据:(xi-)2=17.5,(xi-)(yi-)=35,≈36.5.
参考公式:相关系数r=;
回归直线方程为=x+,
其中=,=-.
[解] (1)作出散点图如下.
∵==16,
∴(yi-)2=76,
∴r==
=≈≈0.96.
∴两变量之间具有较强的线性相关关系,故可用线性回归模型拟合市场占有率y与月份代码x之间的关系.
(2)由参考数据及(1)知===2,
==3.5,
∴=-=16-2×3.5=9,
∴y关于x的线性回归方程为=2x+9.
2019年3月的月份代码为x=10,∴=2×10+9=29,
∴估计该公司2019年3月份的市场占有率为29%.
[类题通法]
1.求线性回归方程的步骤
(1)计算,;
(2)计算iyi,;
(3)计算==;
=-;
(4)写出线性回归方程=x+.
[注意] 样本点的中心(,)必在回归直线上.
2.相关系数r
(1)当r>0时,表明两个变量正相关;
当r<0时,表明两个变量负相关.
(2)r的绝对值越接近于1,表明两个变量的线性相关性越强.r的绝对值越接近于0,表明两个变量之间几乎不存在线性相关关系.通常|r|大于0.75时,认为两个变量有很强的线性相关性.
角度二 非线性回归分析
某机构为研究某种图书每册的成本费y(单位:元)与印刷数量x(单位:千册)的关系,收集了一些数据并进行了初步处理,得到了下面的散点图及一些统计量的值.
(xi-)2 | (xi-)(yi-) | (ui-)2 | (ui-)(yi-) | |||
15.25 | 3.63 | 0.269 | 2 085.5 | -230.3 | 0.787 | 7.049 |
表中ui=,=i.
(1)根据散点图判断:y=a+bx与y=c+哪一个模型更适合作为该图书每册的成本费y(单位:元)与印刷数量x(单位:千册)的回归方程?(只要求给出判断,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立y关于x的回归方程(回归系数的结果精确到0.01).
(3)若该图书每册的定价为10元,则至少应该印刷多少册才能使销售利润不低于78 840元?(假设能够全部售出.结果精确到1)
附:对于一组数据(ω1,ν1),(ω2,ν2),…,(ωn,νn),其回归直线=+ω的斜率和截距的最小二乘估计分别为=,=-.
[解] (1)由散点图判断,y=c+更适合作为该图书每册的成本费y(单位:元)与印刷数量x(单位:千册)的回归方程.
(2)令u=,先建立y关于u的线性回归方程,
由于==≈8.957≈8.96,
∴=-·=3.63-8.957×0.269≈1.22,
∴y关于u的线性回归方程为=1.22+8.96u,
∴y关于x的回归方程为=1.22+.
(3)假设印刷x千册,
依题意得10x-x≥78.840,
∴x≥10,
∴至少印刷10 000册才能使销售利润不低于78 840元.
[类题通法]
解决非线性回归问题的关键是适当换元,将非线性回归分析转化为线性回归分析问题求解.
[综合训练]
1.(2018·全国卷Ⅱ)下图是某地区2000年至2016年环境基础设施投资额y(单位:亿元)的折线图.
为了预测该地区2018年的环境基础设施投资额,建立了y与时间变量t的两个线性回归模型.根据2000年至2016年的数据(时间变量t的值依次为1,2,…,17)建立模型①:=-30.4+13.5t;根据2010年至2016年的数据(时间变量t的值依次为1,2,…,7)建立模型②:=99+17.5t.
(1)分别利用这两个模型,求该地区2018年的环境基础设施投资额的预测值;
(2)你认为用哪个模型得到的预测值更可靠?并说明理由.
解:(1)利用模型①,可得该地区2018年的环境基础设施投资额的预测值为=-30.4+13.5×19=226.1(亿元).
利用模型②,可得该地区2018年的环境基础设施投资额的预测值为=99+17.5×9=256.5(亿元).
(2)利用模型②得到的预测值更可靠.
理由如下:
(ⅰ)从折线图可以看出,2000年至2016年的数据对应的点没有随机散布在直线y=-30.4+13.5t上下,这说明利用2000年至2016年的数据建立的线性模型①不能很好地描述环境基础设施投资额的变化趋势.2010年相对2009年的环境基础设施投资额有明显增加,2010年至2016年的数据对应的点位于一条直线的附近,这说明从2010年开始环境基础设施投资额的变化规律呈线性增长趋势,利用2010年至2016年的数据建立的线性模型=99+17.5t可以较好地描述2010年以后的环境基础设施投资额的变化趋势,因此利用模型②得到的预测值更可靠.
(ⅱ)从计算结果看,相对于2016年的环境基础设施投资额220亿元,由模型①得到的预测值226.1亿元的增幅明显偏低,而利用模型②得到的预测值的增幅比较合理,说明利用模型②得到的预测值更可靠.
(以上给出了2种理由,考生答出其中任意一种或其他合理理由均可得分)
2.某市春节期间7家超市的广告费支出xi(万元)和销售额yi(万元)数据如下:
超市 | A | B | C | D | E | F | G |
广告费支出x | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
销售额y | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
(1)若用线性回归模型拟合y与x的关系,求y关于x的线性回归方程;
(2)若用二次函数回归模型拟合y与x的关系,可得回归方程为=-0.17x2+5x+20,经计算二次函数回归模型和线性回归模型的R2分别约为0.92和0.75,请用R2说明选择哪个回归模型更合适,并用此模型预测A超市广告费支出为3万元时的销售额.
参数数据及公式:=8,=42,iyi=2 794,
=708,=,=-.
解:(1)∵===1.7,
∴=-=42-1.7×8=28.4.
∴y关于x的线性回归方程是=1.7x+28.4.
(2)∵0.75<0.92,
∴二次函数回归模型更合适.
当x=3万元时,=-0.17×9+5×3+20=33.47,
∴预测A超市销售额为33.47万元.
独立性检验 |
[由题知法]
(2018·郑州质量预测)2018年10月份郑州市进行了高三学生的体育学业水平测试,为了考察高中学生的身体素质情况,现抽取了某校1 000名(男生800名,女生200名)学生的测试成绩,根据性别按分层抽样的方法抽取100名学生的测试成绩进行分析,得到如下统计表:
男生测试情况:
抽样情况 | 病残免试 | 不合格 | 合格 | 良好 | 优秀 |
人数 | 5 | 10 | 15 | 47 | x |
女生测试情况:
抽样情况 | 病残免试 | 不合格 | 合格 | 良好 | 优秀 |
人数 | 2 | 3 | 10 | y | 2 |
(1)现从抽取的100名且测试等级为“优秀”的学生中随机选出2名学生,求选出的这2名学生恰好是一男一女的概率;
(2)若测试等级为“良好”或“优秀”的学生为“体育达人”,其他等级(含病残免试)的学生为“非体育达人”,根据以上统计数据填写下面列联表,并回答能否在犯错误的概率不超过0.010的前提下认为“是否为‘体育达人’与性别有关?”
| 男性 | 女性 | 总计 |
体育达人 |
|
|
|
非体育达人 |
|
|
|
总计 |
|
|
|
临界值表:
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
附:K2=,其中n=a+b+c+d.
[解] (1)按分层抽样的方法男生应抽取80名,女生应抽取20名,
∴x=80-(5+10+15+47)=3,y=20-(2+3+10+2)=3.
抽取的100名且测试等级为“优秀”的3名男生分别记为A,B,C,2名女生分别记为a, b.
从5名学生中任选2名,总的基本事件有(A,B),(A,C),(A,a),(A,b),(B,C),(B,a),(B,b),(C,a),(C,b),(a,b),共10个.
设“选出的2名学生恰好是一男一女”为事件M,
则事件M包含的基本事件有(A,a),(A,b),(B,a),(B,b),(C,a),(C,b),共6个,
∴P(A)==.
(2)2×2列联表如下:
| 男生 | 女生 | 总计 |
体育达人 | 50 | 5 | 55 |
非体育达人 | 30 | 15 | 45 |
总计 | 80 | 20 | 100 |
则K2=
=≈9.091.
∵9.091>6.635且P(K2≥6.635)=0.010,
∴能在犯错误的概率不超过0.010的前提下认为“是否为‘体育达人’与性别有关”.
[类题通法] 独立性检验的关键
(1)根据2×2列联表准确计算K2的观测值k,若2×2列联表没有列出来,要先列出此表.
(2)K2的观测值k越大,对应假设事件H0成立(两类变量相互独立)的概率越小,H0不成立的概率越大.
[应用通关]
2018年2月22日上午,山东省委、省政府在济南召开山东省全面展开新旧动能转换重大工程动员大会,会议动员各方力量,迅速全面展开新旧动能转换重大工程.某企业响应号召,对现有设备进行改造,为了分析设备改造前后的效果,现从设备改造前后生产的大量产品中各抽取了200件产品作为样本,检测一项质量指标值,若该项质量指标值落在[20,40)内的产品视为合格品,否则为不合格品.设备改造前的样本的频率分布直方图和设备改造后的样本的频数分布表如下所示.
设备改造后样本的频数分布表:
质量指标值 | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) | [40,45] |
频数 | 4 | 36 | 96 | 28 | 32 | 4 |
(1)完成下面的2×2列联表,并判断是否有99%的把握认为该企业生产的这种产品的质量指标值与设备改造有关;
| 设备改造前 | 设备改造后 | 总计 |
合格品 |
|
|
|
不合格品 |
|
|
|
总计 |
|
|
|
(2)根据上述数据,试从产品合格率的角度对改造前后设备的优劣进行比较;
(3)根据市场调查,设备改造后,每生产一件合格品企业可获利180元,一件不合格品亏损100元,用频率估计概率,求生产1 000件产品企业大约能获利多少元?
附:
P(K2≥k0) | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
K2=,n=a+b+c+d.
解:(1)根据题中图和表得到2×2列联表:
| 设备改造前 | 设备改造后 | 总计 |
合格品 | 172 | 192 | 364 |
不合格品 | 28 | 8 | 36 |
总计 | 200 | 200 | 400 |
将2×2列联表中的数据代入公式得
K2=≈12.210.
∵12.210>6.635,
∴有99%的把握认为该企业生产的这种产品的质量指标值与设备改造有关.
(2)由2×2列联表可知,
设备改造后产品的合格率约为=0.96,
设备改造前产品的合格率约为=0.86,
即设备改造后产品的合格率更高,因此,设备改造后性能更好.
(3)用频率估计概率,1 000件产品中大约有960件合格品,40件不合格品,则180×960-100×40=168 800,
∴该企业大约能获利168 800元.
[专题跟踪检测](对应配套卷P200)
1.在一次马拉松比赛中,35名运动员的成绩(单位:分钟)的茎叶图如图所示.
若将运动员按成绩由好到差编为1~35号,再用系统抽样方法从中抽取7人,则其中成绩在区间[139,151]上的运动员人数是( )
A.3 B.4
C.5 D.6
解析:选B 由系统抽样可知,35人分为7组,每组5人,最后一组成绩均大于151,前两组成绩均小于139,故成绩在区间[139,151]上的运动员人数为4.
2.“双色球”彩票中红色球的号码由编号为01,02,…,33的33个个体组成,一位彩民利用下面的随机数表选取6组数作为6个红色球的编号,选取方法是从随机数表第1行的第6列和第7列数字开始由左到右依次选取两个数字,则选出来的第6个红色球的编号为( )
49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 26 34 91 64 |
57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76 |
A.23 B.09
C.02 D.17
解析:选C 从随机数表第1行的第6列和第7列数字开始由左到右依次选取两个数字,则选出的6个红色球的编号依次为21,32,09,16,17,02,故选出的第6个红色球的编号为02.故选C.
3.(2018·昆明调研)下图是1951~2016年我国年平均气温变化图.
根据上图,判断下列结论正确的是( )
A.1951年以来,我国年平均气温逐年增高
B.1951年以来,我国年平均气温在2016年再创新高
C.2000年以来,我国年平均气温都高于1981~2010年的平均值
D.2000年以来,我国年平均气温的平均值高于1981~2010年的平均值
解析:选D 由1951~2016年我国年平均气温变化图可以看出,年平均气温有升高的也有降低的,所以选项A不正确;2016年的年平均气温不是最高的,所以选项B不正确;2012年的年平均气温低于1981~2010年的平均值,所以选项C不正确;2000年以来,只有2012年的年平均气温低于1981~2010年的平均值,所以2000年以来,我国年平均气温的平均值高于1981~2010年的平均值,故选项D正确,故选D.
4.(2018·惠州模拟)某商场为了了解毛衣的月销售量y(件)与月平均气温x(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
月平均气温x/℃ | 17 | 13 | 8 | 2 |
月销售量y/件 | 24 | 33 | 40 | 55 |
由表中数据算出线性回归方程=x+中的=-2,气象部门预测下个月的平均气温约为6 ℃,据此估计该商场下个月毛衣销售量约为( )
A.46件 B.40件
C.38件 D.58件
解析:选A 由题中数据,得=10,=38,回归直线=x+过点(,),且=-2,代入得=58,则回归方程=-2x+58,所以当x=6时,y=46,故选A.
5.(2018·郑州质量预测)我市某高中从高三年级甲、乙两个班中各选出7名学生参加2018年全国高中数学联赛(河南初赛),他们取得的成绩(满分140分)的茎叶图如图所示,其中甲班学生成绩的中位数是81,乙班学生成绩的平均数是86,若正实数a,b满足a,G,b成等差数列且x,G,y成等比数列,则+的最小值为( )
A. B.2
C. D.9
解析:选C 由甲班学生成绩的中位数是81,可知81为甲班7名学生的成绩按从小到大的顺序排列的第4个数,故x=1.由乙班学生成绩的平均数为86,可得(-10)+(-6)+(-4)+(y-6)+5+7+10=0,解得y=4.由x,G,y成等比数列,可得G2=xy=4,由正实数a,b满足a,G,b成等差数列,可得G=2,a+b=2G=4,所以+=(a+b)=≥×(5+4)=(当且仅当b=2a时取等号).故+的最小值为,选C.
6.某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据频率分布直方图,这200名学生中每周的自习时间不少于22.5小时的人数是( )
A.56 B.60
C.120 D.140
解析:选D 由频率分布直方图可知,每周的自习时间不少于22.5小时的频率为(0.16+0.08+0.04)×2.5=0.7,所以每周的自习时间不少于22.5小时的人数是200×0.7=140.
7.空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~300为重度污染;大于300为严重污染.从某地一环保人士某年的AQI记录数据中,随机抽取10个,其茎叶图记录如图所示.根据该统计数据,估计此地该年AQI大于100的天数约为__________.(该年为365天)
解析:该样本中AQI大于100的频数是4,频率为,由此估计该地全年AQI大于100的概率为,估计此地该年AQI大于100的天数约为365×=146.
答案:146
8.某学校高二年级共有女生300人,现调查她们每天的课外运动时间,发现她们的课外运动时间介于30分钟到90分钟,如图是统计结果的频率分布直方图,则她们的平均运动时间大约是________分钟.
解析:由题图得平均运动时间约为35×0.1+45×0.1+55×0.5+65×0.2+75×0.05+85×0.05=56.5(分钟).
答案:56.5
9.如图所示的茎叶图记录了甲、乙两位射箭运动员的5次比赛成绩(单位:环),若两位运动员平均成绩相同,则成绩较为稳定(方差较小)的那位运动员成绩的方差为________.
解析:由题意知=90,
则=90,
解得x=2,
所以s=×[(87-90)2+(89-90)2+(90-90)2+(91-90)2+(93-90)2]=4,
s= ×[(88-90)2+(89-90)2+(90-90)2+(91-90)2+(92-90)2]=2,
所以s>s,所以成绩较为稳定(方差较小)的那位运动员成绩的方差为2.
答案:2
10.某公司为了解广告投入对销售收益的影响,在若干地区共投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.
(1)根据频率分布直方图,计算图中各小矩形的宽度;
(2)试估计该公司投入4万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入x/万元 | 1 | 2 | 3 | 4 | 5 |
销售收益y/万元 | 2 | 3 | 2 |
| 7 |
由表中的数据显示,x与y之间存在线性相关关系,请将(2)的结果填入空白栏,并求出y关于x的回归直线方程.
附:=,=-.
解:(1)设各小矩形的宽度为m,由频率分布直方图中各小矩形的面积和为1,可知(0.08+0.10+0.14+0.12+0.04+0.02)·m=1,
解得m=2,
故图中各小矩形的宽度为2.
(2)由(1)知各分组依次是[0,2),[2,4),[4,6),[6,8),[8,10),[10,12],它们的中点的横坐标分别为1,3,5,7,9,11,
各组对应的频率分别为0.16,0.20,0.28,0.24,0.08,0.04,
故可估计销售收益的平均值为1×0.16+3×0.20+5×0.28+7×0.24+9×0.08+11×0.04=5.
(3)由(2)可知空白栏中填5,
由题意可知,==3,
==3.8,
iyi=1×2+2×3+3×2+4×5+5×7=69,
=12+22+32+42+52=55,
所以==1.2,
=3.8-1.2×3=0.2,
故所求的回归直线方程为=1.2x+0.2.
11.(2018·全国卷Ⅲ)某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人.第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:
(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由.
(2)求40名工人完成生产任务所需时间的中位数m,并将完成生产任务所需时间超过m和不超过m的工人数填入下面的列联表:
| 超过m | 不超过m |
第一种生产方式 |
|
|
第二种生产方式 |
|
|
(3)根据(2)中的列联表,能否有99%的把握认为两种生产方式的效率有差异?
附:K2=,
解:(1)第二种生产方式的效率更高.
理由如下:
(ⅰ)由茎叶图可知:用第一种生产方式的工人中,有75%的工人完成生产任务所需时间至少80 min,用第二种生产方式的工人中,有75%的工人完成生产任务所需时间至多79 min.因此第二种生产方式的效率更高.
(ⅱ)由茎叶图可知:用第一种生产方式的工人完成生产任务所需时间的中位数为85.5 min,用第二种生产方式的工人完成生产任务所需时间的中位数为73.5 min.因此第二种生产方式的效率更高.
(ⅲ)由茎叶图可知:用第一种生产方式的工人完成生产任务所需平均时间高于80 min;用第二种生产方式的工人完成生产任务所需平均时间低于80 min.因此第二种生产方式的效率更高.
(ⅳ)由茎叶图可知:用第一种生产方式的工人完成生产任务所需时间分布在茎8上的最多,关于茎8大致呈对称分布;用第二种生产方式的工人完成生产任务所需时间分布在茎7上的最多,关于茎7大致呈对称分布.又用两种生产方式的工人完成生产任务所需时间分布的区间相同,故可以认为用第二种生产方式完成生产任务所需的时间比用第一种生产方式完成生产任务所需的时间更少.因此第二种生产方式的效率更高.
(以上给出了4种理由,考生答出其中任意一种或其他合理理由均可得分)
(2)由茎叶图知m==80.
列联表如下:
| 超过m | 不超过m |
第一种生产方式 | 15 | 5 |
第二种生产方式 | 5 | 15 |
(3)因为K2==10>6.635,所以有99%的把握认为两种生产方式的效率有差异.
12.在一次抽样调查中测得样本的6组数据,得到一个变量y关于x的回归方程模型,其对应的数值如下表:
x | 2 | 3 | 4 | 5 | 6 | 7 |
y | 3.00 | 2.48 | 2.08 | 1.86 | 1.48 | 1.10 |
(1)请用相关系数r说明y与x之间存在线性相关关系(当|r|>0.75时,说明y与x之间具有线性相关关系);
(2)根据(1)的判断结果,建立y关于x的回归直线方程并预测当x=9时,对应的值为多少(精确到0.01).
附:回归直线方程为=x+,
其中=,=-,
相关系数r的公式为r=.
参考数据:
iyi=47.64,=139,(xi-)(yi-)=-6.36,
≈4.18, ≈1.53.
解:(1)由题意,得=×(2+3+4+5+6+7)=4.5,
=×(3.00+2.48+2.08+1.86+1.48+1.10)=2,
又(xi-)(yi-)=-6.36, ≈4.18,≈1.53,
所以r=≈≈-0.99.
因为|r|>0.75,所以y与x之间存在线性相关关系.
(2)因为==
≈-0.363≈-0.36,
=-=2+0.363×4.5≈3.63,
所以y关于x的线性回归方程为=-0.36x+3.63.
将x=9代入回归方程得=-0.36×9+3.63=0.39.
13.(2019届高三·广州调研)某基地蔬菜大棚采用无土栽培方式种植各类蔬菜.过去50周的资料显示,该地周光照量X(单位:小时)都在30小时以上,其中不足50小时的有5周,不低于50小时且不超过70小时的有35周,超过70小时的有10周.根据统计,该基地的西红柿增加量y(千克)与使用某种液体肥料的质量x(千克)之间的对应数据为如图所示的折线图.
(1)依据折线图计算相关系数r(精确到0.01),并据此判断是否可用线性回归模型拟合y与x的关系.(若|r|>0.75,则线性相关程度很高,可用线性回归模型拟合)
(2)蔬菜大棚对光照要求较高,某光照控制仪商家为该基地提供了部分光照控制仪,但每周光照控制仪运行台数受周光照量X限制,并有如下关系:
周光照量X/小时 | 30<X<50 | 50≤X≤70 | X>70 |
光照控制仪运行台数 | 3 | 2 | 1 |
对商家来说,若某台光照控制仪运行,则该台光照控制仪产生的周利润为3 000元;若某台光照控制仪未运行,则该台光照控制仪周亏损1 000元.若商家安装了3台光照控制仪,求商家在过去50周的周总利润的平均值.
附:相关系数公式:r=,
参考数据:≈0.55,≈0.95.
解:(1)由已知数据可得==5,
==4.
因为(xi-)(yi-)=(-3)×(-1)+0+0+0+3×1=6,
==2,
==,
所以相关系数r=
==≈0.95.
因为|r|>0.75,
所以可用线性回归模型拟合y与x的关系.
(2)由条件可得在过去50周里,
当X>70时,共有10周,此时只有1台光照控制仪运行,
每周的周总利润为1×3 000-2×1 000=1 000(元).
当50≤X≤70时,共有35周,此时有2台光照控制仪运行,
每周的周总利润为2×3 000-1×1 000=5 000(元).
当30<X<50时,共有5周,此时3台光照控制仪都运行,
每周的周总利润为3×3 000=9 000(元).
所以过去50周的周总利润的平均值为
=4 600(元),
所以商家在过去50周的周总利润的平均值为4 600元.









