2019-2020学年广东省广州市花都区七年级下学期期末数学试卷 （解析版）

2019-2020学年广东广州市花都区七年级第二学期期末数学试卷
一、选择题（共10小题）.
1．下列各数中，无理数是（　　）
A． B．﹣4 C．1.732 D．
2．以下坐标所对应的点在第一象限的是（　　）
A．（1，2） B．（﹣1，2） C．（﹣1，﹣2） D．（1，﹣2）
3．下列哪组数值是二元一次方程x+y＝3的解（　　）
A． B． C． D．
4．数值在2和3之间的数是（　　）
A． B． C． D．
5．已知不等式组的解集如图所示，则不等式组的整数解个数为（　　）

A．2个 B．3个 C．4个 D．5个
6．如图，△ABC沿BC所在直线向右平移得到△DEF，已知EC＝2，BF＝8，则CF的长为（　　）

A．3 B．4 C．5 D．6
7．已知x＜y，则下列结论不成立的是（　　）
A．x﹣2＜y﹣2 B．3x+1＜3y+1 C．﹣2x＜﹣2y D．
8．要反映花都区六月上旬每天的最高气温的变化趋势，最宜采用（　　）
A．折线图 B．条形图 C．扇形图 D．直方图
9．如图，直线AB，CD相交于点O，已知∠AOC＝80°，∠BOE：∠EOD＝3：2，则∠AOE的度数是（　　）

A．100° B．116° C．120° D．132°
10．已知关于x、y的方程组，若x﹣y＝8，则a的值为（　　）
A．1 B．2 C．4 D．6
二、填空题（共6小题）.
11．不等式x﹣2＞0的解集是　 　．
12．一个正数的两个平方根是a﹣4和3，则a＝　 　．
13．把命题“等角的补角相等”改写成“如果…那么…”的形式是　 　．
14．若点A（a，3）到y轴的距离为2，则a＝　 　．
15．若不等式组的解集为3≤x≤4，则a+b＝　 　．
16．如图，已知A1（1，2），A2（2，2），A3（3，0），A4（4，﹣2），A5（5，﹣2），A6（6，0）…，按这样的规律，则点A2020的坐标为　 　．

三、解答题（本大题共9题，满分72分.解答须写出文字说明、证明过程和演算步骤.）
17．计算+．
18．如图，已知∠1＝∠2，∠3＝50°，求∠ABE的度数．

19．解方程组：
20．解不等式组，并在数轴上表示解集．

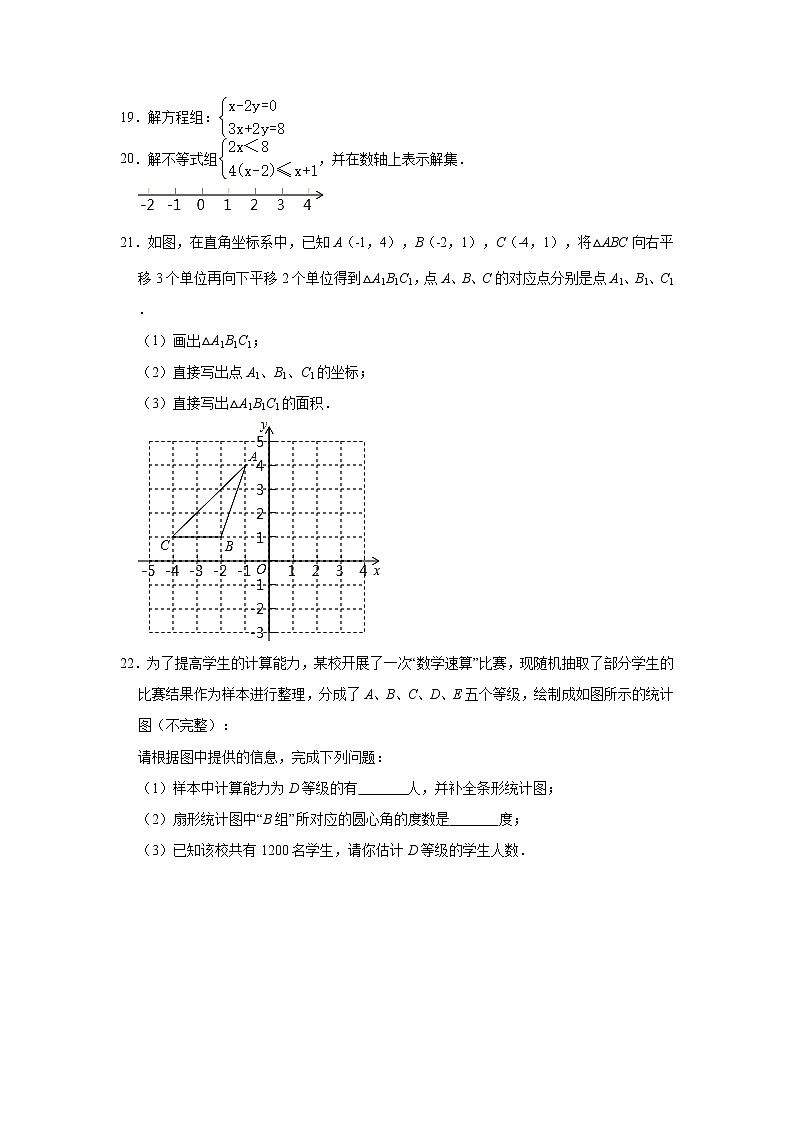
21．如图，在直角坐标系中，已知A（﹣1，4），B（﹣2，1），C（﹣4，1），将△ABC向右平移3个单位再向下平移2个单位得到△A1B1C1，点A、B、C的对应点分别是点A1、B1、C1．
（1）画出△A1B1C1；
（2）直接写出点A1、B1、C1的坐标；
（3）直接写出△A1B1C1的面积．

22．为了提高学生的计算能力，某校开展了一次“数学速算”比赛，现随机抽取了部分学生的比赛结果作为样本进行整理，分成了A、B、C、D、E五个等级，绘制成如图所示的统计图（不完整）：
请根据图中提供的信息，完成下列问题：
（1）样本中计算能力为D等级的有　 　人，并补全条形统计图；
（2）扇形统计图中“B组”所对应的圆心角的度数是　 　度；
（3）已知该校共有1200名学生，请你估计D等级的学生人数．

23．如图，已知∠1+∠2＝180°，∠3＝∠4，试判断EF与AC的位置关系，并加以证明．

24．某学校准备购买体育教学用的器材A和B，下表是这两种器材的价格信息：
A
B
总费用
3件
1件
500元
1件
2件
250元
（1）求每件器材A、器材B的销售价格；
（2）若该学校准备用不多于2700元的金额购买这两种器材共25件，且购买器材A不少于12件，则有哪几种购买方案，并求出最少费用是多少元？
25．如图1，在平面直角坐标系中，A（4，0），B（0，4），C是第一象限内一点，且BC∥x轴．
（1）连接AC，当S△ABC＝6时，求点C的坐标；
（2）设D为y轴上一动点，连接AD，CD，作∠BCD、∠DAO的平分线相交于点P，在点D的运动过程中，试判断等式∠CPA＝2∠CDA是否始终成立，并说明理由．



参考答案
一、选择题（共10小题）.
1．下列各数中，无理数是（　　）
A． B．﹣4 C．1.732 D．
解：A.是分数，属于有理数；
B．﹣4是整数，属于有理数；
C.1.732是有限小数，属于有理数；
D.是无理数．
故选：D．
2．以下坐标所对应的点在第一象限的是（　　）
A．（1，2） B．（﹣1，2） C．（﹣1，﹣2） D．（1，﹣2）
解：A．（1，2）在第一象限；
B．（﹣1，2）在第二象限；
C．（﹣1，﹣2）在第三象限；
D．（1，﹣2）在第四象限；
故选：A．
3．下列哪组数值是二元一次方程x+y＝3的解（　　）
A． B． C． D．
解：A、把代入方程得：左边＝2﹣1＝1，右边＝3，
左边≠右边，即不是方程x+y＝3的解；
B、把代入方程得：左边＝2+1＝3，右边＝3，
左边＝右边，即是方程x+y＝3的解；
C、把代入方程得：左边＝﹣4+1＝﹣3，右边＝3，
左边≠右边，即不是方程x+y＝3的解；
D、把代入方程得：左边＝﹣1﹣2＝﹣3，右边＝3，
左边≠右边，即不是方程x+y＝3的解．
故选：B．
4．数值在2和3之间的数是（　　）
A． B． C． D．
解：A、1＜＜2，不在2和3之间，故本选项不符合题意；
B、1＜＜2，不在2和3之间，故本选项不符合题意；
C、2＜＜3，在2和3之间，故本选项符合题意；
D、3＜＜4，不在2和3之间，故本选项不符合题意；
故选：C．
5．已知不等式组的解集如图所示，则不等式组的整数解个数为（　　）

A．2个 B．3个 C．4个 D．5个
解：由数轴知，不等式组的整数解为﹣1、0、1、2，
故选：C．
6．如图，△ABC沿BC所在直线向右平移得到△DEF，已知EC＝2，BF＝8，则CF的长为（　　）

A．3 B．4 C．5 D．6
解：由平移的性质可知，BC＝EF，
∴BE＝CF，
∵BF＝8，EC＝2，
∴BE+CF＝8﹣2＝6，
∴CF＝BE＝3，
故选：A．
7．已知x＜y，则下列结论不成立的是（　　）
A．x﹣2＜y﹣2 B．3x+1＜3y+1 C．﹣2x＜﹣2y D．
解：A．∵x＜y，
∴x﹣2＜y﹣2，故本选项不合题意；
B．∵x＜y，
∴3x+1＜3y+1，故本选项不合题意；
C．∵x＜y，
∴﹣2x＞﹣2y，故本选项符合题意；
D．∵x＜y，
∴，故本选项不合题意．
故选：C．
8．要反映花都区六月上旬每天的最高气温的变化趋势，最宜采用（　　）
A．折线图 B．条形图 C．扇形图 D．直方图
解：根据题意，要反映花都区六月上旬每天的最高气温的变化趋势，结合统计图各自的特点，应选择折线统计图．
故选：A．
9．如图，直线AB，CD相交于点O，已知∠AOC＝80°，∠BOE：∠EOD＝3：2，则∠AOE的度数是（　　）

A．100° B．116° C．120° D．132°
解：∵∠AOC＝80°，
∴∠DOB＝80°，∠AOD＝100°，
∵∠BOE：∠EOD＝3：2，
∴∠DOE＝80°×＝32°，
∴∠AOE＝100°+32°＝132°，
故选：D．
10．已知关于x、y的方程组，若x﹣y＝8，则a的值为（　　）
A．1 B．2 C．4 D．6
解：，
②﹣①得，x﹣y＝4a，
∵x﹣y＝8，
∴4a＝8，
解得a＝2．
故选：B．
二、填空题（本大题共6题，每题3分，满分18分.）
11．不等式x﹣2＞0的解集是　x＞2　．
解：对不等式x﹣2＞0移项得：
x＞2．
故答案为：x＞2．
12．一个正数的两个平方根是a﹣4和3，则a＝　1　．
【解答】结：由题意得a﹣4+3＝0，
解得a＝1，
故答案为1．
13．把命题“等角的补角相等”改写成“如果…那么…”的形式是　如果两个角是等角，那么它们的补角相等　．
解：题设为：两个角是等角，结论为：它们的补角相等，
故写成“如果…那么…”的形式是：如果两个角是等角，那么它们的补角相等．
故答案为：如果两个角是等角，那么它们的补角相等．
14．若点A（a，3）到y轴的距离为2，则a＝　±2　．
解：∵点A（a，3）到y轴的距离为2，
∴a＝±2．
故答案为：＝±2．
15．若不等式组的解集为3≤x≤4，则a+b＝　1　．
解：解不等式x+a≥0，得：x≥﹣a，
解不等式x﹣b≤0，得：x≤b，
∵不等式组的解集为3≤x≤4，
∴a＝﹣3，b＝4，
则a+b＝﹣3+4＝1，
故答案为：1．
16．如图，已知A1（1，2），A2（2，2），A3（3，0），A4（4，﹣2），A5（5，﹣2），A6（6，0）…，按这样的规律，则点A2020的坐标为　（2020，﹣2）　．

解：观察发现，每6个点形成一个循环，
∵A6（6，0），
∴OA6＝6，
∵2020÷6＝336…4，
∴点A2020的位于第337个循环组的第4个，
∴点A2020的横坐标为6×336+4＝2020，其纵坐标为：﹣2，
∴点A2020的坐标为（2020，﹣2）．
故答案为：（2020，﹣2）．
三、解答题（本大题共9题，满分72分.解答须写出文字说明、证明过程和演算步骤.）
17．计算+．
解：原式＝4﹣2＝2．
18．如图，已知∠1＝∠2，∠3＝50°，求∠ABE的度数．

解：∵∠1＝∠2，
∴AB∥CF，
∴∠ABC＝∠3＝50°，
∴∠ABE＝180°﹣∠ABC＝180°﹣50°＝130°．
19．解方程组：
解：由（1），得x＝2y． （3）
把（3）代入（2），得3•2y+2y＝8，
解得y＝1．
把y＝1代入（3），得x＝2．
∴原方程组的解是．
20．解不等式组，并在数轴上表示解集．

解：解不等式2x＜8，得：x＜4，
解不等式4（x﹣2）≤x+1，得：x≤3，
则不等式组解集为x≤3，
将不等式组的解集表示在数轴上如下：

21．如图，在直角坐标系中，已知A（﹣1，4），B（﹣2，1），C（﹣4，1），将△ABC向右平移3个单位再向下平移2个单位得到△A1B1C1，点A、B、C的对应点分别是点A1、B1、C1．
（1）画出△A1B1C1；
（2）直接写出点A1、B1、C1的坐标；
（3）直接写出△A1B1C1的面积．

解：（1）如图所示：△A1B1C1，即为所求；

（2）A1（2，2），B1（1，﹣1），C1（﹣1，﹣1）；

（3）△A1B1C1的面积为：×2×3＝3．

22．为了提高学生的计算能力，某校开展了一次“数学速算”比赛，现随机抽取了部分学生的比赛结果作为样本进行整理，分成了A、B、C、D、E五个等级，绘制成如图所示的统计图（不完整）：
请根据图中提供的信息，完成下列问题：
（1）样本中计算能力为D等级的有　70　人，并补全条形统计图；
（2）扇形统计图中“B组”所对应的圆心角的度数是　126　度；
（3）已知该校共有1200名学生，请你估计D等级的学生人数．

解：（1）本次调查的学生有：40÷20%＝200（人），
样本中计算能力为D等级的有：200﹣14﹣40﹣56﹣20＝70（人），
补全的条形统计图如右图所示，
故答案为：70；
（2）扇形统计图中“B组”所对应的圆心角的度数是：360°×＝126°，
故答案为：126；
（3）1200×＝420（人），
即D等级的学生有420人．

23．如图，已知∠1+∠2＝180°，∠3＝∠4，试判断EF与AC的位置关系，并加以证明．

解：EF∥AC，
证明：∵∠1+∠2＝180°，∠1+∠ADC＝180°，
∴∠ADC＝∠2，
∴AD∥BC，
∴∠3＝∠ACB，
∵∠3＝∠4，
∴∠ACB＝∠4，
∴EF∥AC．
24．某学校准备购买体育教学用的器材A和B，下表是这两种器材的价格信息：
A
B
总费用
3件
1件
500元
1件
2件
250元
（1）求每件器材A、器材B的销售价格；
（2）若该学校准备用不多于2700元的金额购买这两种器材共25件，且购买器材A不少于12件，则有哪几种购买方案，并求出最少费用是多少元？
解：（1）设每件器材A的销售价格为x元，每件器材B的销售价格为y元，
依题意，得：，
解得：．
答：每件器材A的销售价格为150元，每件器材B的销售价格为50元．
（2）设购买m件器材A，则购买（25﹣m）件器材B，
依题意，得：，
解得：12≤m≤14，
∵m为正整数，
∴m可以取12，13，14，
∴共有3种购买方案，方案1：购买12件器材A，13件器材B；方案2：购买13件器材A，12件器材B；方案3：购买14件器材A，11件器材B．
方案1所需费用为150×12+50×13＝2450（元）；
方案2所需费用为150×13+50×12＝2550（元）；
方案3所需费用为150×14+50×11＝2650（元）．
∵2450＜2550＜2650，
∴最少费用是2450元．
答：共有3种购买方案，方案1：购买12件器材A，13件器材B；方案2：购买13件器材A，12件器材B；方案3：购买14件器材A，11件器材B．最少费用是2450元．
25．如图1，在平面直角坐标系中，A（4，0），B（0，4），C是第一象限内一点，且BC∥x轴．
（1）连接AC，当S△ABC＝6时，求点C的坐标；
（2）设D为y轴上一动点，连接AD，CD，作∠BCD、∠DAO的平分线相交于点P，在点D的运动过程中，试判断等式∠CPA＝2∠CDA是否始终成立，并说明理由．

解：（1）∵B（0，4），C是第一象限内一点，且BC∥x轴，

∴OB＝4，
∵S△ABC＝BC•OB＝6，
∴BC＝3，
∴C（3，4）；
（2））等式∠CPA＝2∠CDA始终成立；理由如下：

连接AC，如图2所示：
∵AP是∠OAD的平分线，
∴∠DAP＝∠DAO＝（90°﹣∠BDC）＝45°﹣∠BDC，
∵PC是∠BCD的角平分线，
∴∠PCD＝∠BCD＝（90°﹣∠ADO）＝45°﹣ADO，
在△PAC中，∠CPA＝180°﹣（∠PAC+∠PCA）
＝180°﹣（∠DAC+∠DCA+∠DAO+BCD）
＝180°﹣（180°﹣∠ADC+45°﹣∠ADO+45°﹣BDC）
＝∠ADC+（∠ADO+∠BDC）﹣90°
＝∠ADC+（180°﹣∠ADC）﹣90°，
＝∠ADC﹣ADC
＝∠ADC，
∴2∠CPA＝∠CDA．
∴在点D的运动过程中，等式∠CPA＝2∠CDA始终成立．