北师大版九年级上册第一章 特殊平行四边形综合与测试课后作业题

这是一份北师大版九年级上册第一章 特殊平行四边形综合与测试课后作业题，共6页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

章末复习


一、选择题


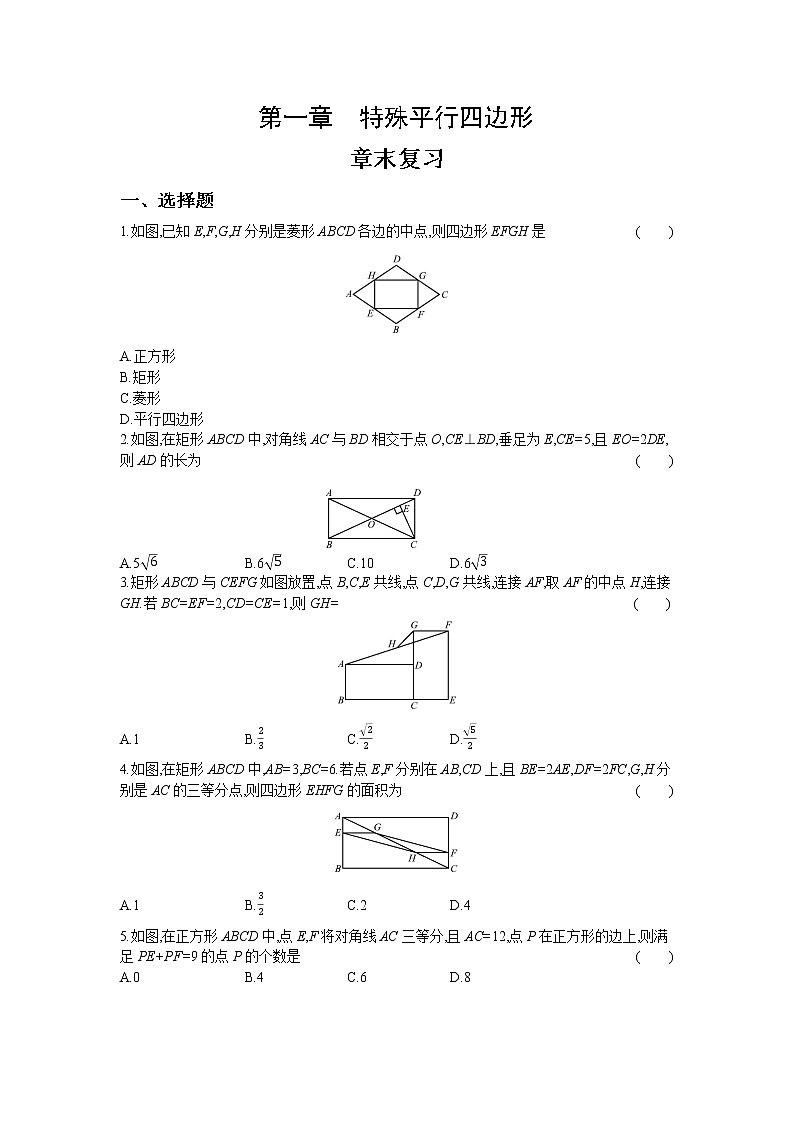
1.如图,已知E,F,G,H分别是菱形ABCD各边的中点,则四边形EFGH是( )





A.正方形


B.矩形


C.菱形


D.平行四边形


2.如图,在矩形ABCD中,对角线AC与BD相交于点O,CE⊥BD,垂足为E,CE=5,且EO=2DE,则AD的长为( )


A.56B.65C.10D.63


3.矩形ABCD与CEFG如图放置,点B,C,E共线,点C,D,G共线,连接AF,取AF的中点H,连接GH.若BC=EF=2,CD=CE=1,则GH= ( )





A.1B.23C.22D.52


4.如图,在矩形ABCD中,AB=3,BC=6.若点E,F分别在AB,CD上,且BE=2AE,DF=2FC,G,H分别是AC的三等分点,则四边形EHFG的面积为( )





A.1B.32C.2D.4


5.如图,在正方形ABCD中,点E,F将对角线AC三等分,且AC=12,点P在正方形的边上,则满足PE+PF=9的点P的个数是( )


A.0B.4C.6D.8





6.如图,矩形纸片ABCD中,将纸片沿EF折叠,使点C与点A重合,连接CF,则下列结论错误是 ( )





A.∠AEB=∠AFG


B.△ABE≌△AGF


C.四边形AECF是菱形


D.AF=EF


7.在平面直角坐标系中,四边形ABCD的顶点坐标分别是A(-3,0),B(0,2),C(3,0),D(0,-2),则四边形ABCD是( )


A.矩形


B.菱形


C.正方形


D.平行四边形


8.如图,在矩形ABCD中,AB=10,AD=4,点E从点D出发以每秒1个单位的速度向点C运动,以AE为一边在AE的左上方作正方形AEFG.同时垂直于CD的直线MN从点C出发以每秒2个单位的速度向点D运动.当点F落在直线MN上,设运动的时间为t秒,则t的值为( )





A.143B.103C.4D.1


二、填空题


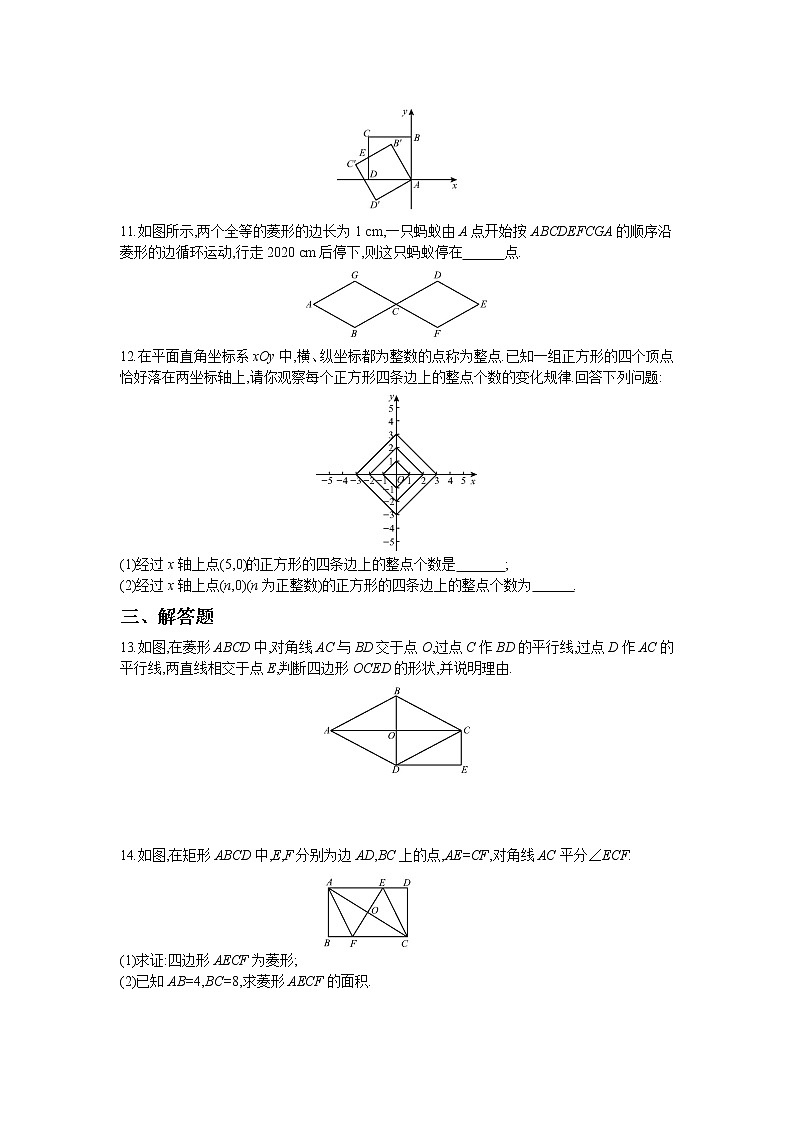
9.如图,在菱形ABCD中,E,F分别是AD,DC的中点.若BD=4,EF=3,则菱形ABCD的周长为 .


10.如图,正方形ABCD的边长为1,点A与原点重合,点B在y轴正半轴上,点D在x轴负半轴上,将正方形ABCD绕着点A逆时针旋转30°得到正方形AB'C'D',CD与B'C'相交于点E,则点E的坐标为 .





11.如图所示,两个全等的菱形的边长为1 cm,一只蚂蚁由A点开始按ABCDEFCGA的顺序沿菱形的边循环运动,行走2020 cm后停下,则这只蚂蚁停在 点.





12.在平面直角坐标系xOy中,横、纵坐标都为整数的点称为整点.已知一组正方形的四个顶点恰好落在两坐标轴上,请你观察每个正方形四条边上的整点个数的变化规律.回答下列问题:





(1)经过x轴上点(5,0)的正方形的四条边上的整点个数是 ;


(2)经过x轴上点(n,0)(n为正整数)的正方形的四条边上的整点个数为 .


三、解答题


13.如图,在菱形ABCD中,对角线AC与BD交于点O,过点C作BD的平行线,过点D作AC的平行线,两直线相交于点E,判断四边形OCED的形状,并说明理由.














14.如图,在矩形ABCD中,E,F分别为边AD,BC上的点,AE=CF,对角线AC平分∠ECF.


(1)求证:四边形AECF为菱形;


(2)已知AB=4,BC=8,求菱形AECF的面积.





15.如图,在矩形ABCD中,AB=8 cm,BC=16 cm,点P从点D出发向点A运动,运动到点A停止,同时,点Q从点B出发向点C运动,运动到点C即停止,点P,Q的速度都是1 cm/s,连接PQ,AQ,CP.设点P,Q运动的时间为t s.


(1)当t为何值时,四边形ABQP是矩形?





(2)当t为何值时,四边形AQCP是菱形?


(3)分别求出(2)中菱形AQCP的周长和面积.














16.如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.


(1)求证:AF=DC;


(2)若AB⊥AC,试判断四边形ADCF的形状,并说明理由.














17.如图,已知正方形ABCD的边长为1,正方形CEFG的面积为S1,点E在DC边上,点G在BC的延长线上,设以线段AD和DE为邻边的矩形的面积为S2,且S1=S2.





(1)求线段CE的长;


(2)若H为BC边的中点,连接HD,求证:HD=HG.





参考答案


一、选择题


8.【提示】过点F作FH⊥CD,交直线CD于点H,则∠EHF=90°,易证△ADE≌△EHF,∴AD=EH=4,由题意得t+2t=4+10,解得t=143.


二、填空题


9. 413


10. -1,33


11. E


12.(1) 20


(2) 4n


三、解答题


13.解:平行四边形OCED是矩形.理由如下:


∵四边形ABCD是菱形,


∴AC⊥BD,∴∠COD=90°.


∵CE∥OD,DE∥OC,


∴四边形OCED是平行四边形.


又∵∠COD=90°,


∴平行四边形OCED是矩形.


14.解:(1)由矩形可得AD∥BC,即AE∥CF,


又∵AE=CF,∴四边形AECF是平行四边形,


∴AF∥CE,∴∠FAC=∠ACE.


∵AC平分∠ECF,∴∠ACE=∠ACF,


∴∠FAC=∠ACF,∴AF=FC,


∴平行四边形AECF是菱形.


(2)设CF=x,则AF=x,BF=8-x,


∵四边形ABCD是矩形,∴∠B=90°,


∴BF2+AB2=AF2,∴(8-x)2+42=x2,


解得x=5,即CF=5,


∴S菱形AECF=CF·AB=5×4=20.


15.解:(1)∵在矩形ABCD中,AB=8 cm,BC=16 cm,


∴BC=AD=16 cm,AB=CD=8 cm,


由已知可得BQ=DP=t cm,AP=CQ=(16-t) cm,在矩形ABCD中,∠B=90°,AD∥BC,


当BQ=AP时,四边形ABQP为矩形,即t=16-t,得t=8,


故当t=8 s时,四边形ABQP为矩形.


(2)∵AP=CQ,AP∥CQ,


∴四边形AQCP为平行四边形,


∴当AQ=CQ时,四边形AQCP为菱形,


即82+t2=16-t时,解得t=6,


故当t=6 s时,四边形AQCP为菱形.


(3)当t=6 s时,AQ=CQ=CP=AP=16-6=10 cm,则周长为4×10=40 cm,面积为10×8=80 cm2.


16.解:(1)∵AF∥BC,∴∠AFE=∠DBE,∠FAE=∠BDE.


∵E是AD的中点,∴AE=DE,


∴△FAE≌△BDE,∴AF=DB.


∵AD是BC边上的中线,


∴DB=DC,∴AF=DC.


(2)四边形ADCF是菱形.


理由:略.


17.解:(1)设正方形CEFG的边长为a,


∵正方形ABCD的边长为1,∴DE=1-a.


∵S1=S2,∴a2=1×(1-a),解得a1=-52-12(舍去),a2=52-12,


即线段CE的长是52-12.


(2)∵H为BC边的中点,BC=1,


∴CH=12,∴DH=52.


∵CH=12,CG=52-12,∴HG=52,


∴HD=HG.


题号
1
2
3
4
5
6
7
8
答案
B
A
C
C
D
D
B
A