湘教版八年级下册第4章 一次函数综合与测试课堂检测

这是一份湘教版八年级下册第4章 一次函数综合与测试课堂检测，共15页。试卷主要包含了如表是加热食用油的温度变化情况，P1，已知一次函数y＝等内容，欢迎下载使用。
一．选择题（共12小题，满分36分，每小题3分）


1．在圆周长的计算公式C＝2πr中，变量有（ ）


A．C，πB．C，rC．π，rD．C，2π


2．在函数y＝中，自变量x的取值范围是（ ）


A．x≥﹣3B．x≥﹣3且x≠0C．x≠0D．x＞﹣3


3．如果直线y＝2x+3和y轴相交于点M，那么M的坐标为（ ）


A．M（2，3）B．M（0，2）C．M（0，）D．M（0，3）


4．如表是加热食用油的温度变化情况：


王红发现，烧了110s时，油沸腾了，则下列说法不正确的是（ ）


A．没有加热时，油的温度是10℃


B．加热50s，油的温度是110℃


C．估计这种食用油的沸点温度约是230℃


D．每加热10s，油的温度升高30℃


5．P1（x1，y1），P2（x2，）是一次函数y＝5x﹣3图象上的两点，则下列判断正确的是（ ）


A．y1＞B．y1＜


C．当x1＜x2时，y1＞D．当x1＜x2时，y1＜


6．已知一次函数y＝（m﹣3）x+6+2m，如果y随自变量x的增大而减小，那么m的取值范围为（ ）


A．m＜3B．m＞3C．m＜﹣3D．m＞﹣3


7．直线y＝﹣2x+6与两坐标轴围成的三角形的面积是（ ）


A．8B．6C．9D．2


8．如图，在平面直角坐标系中点A的坐标为（0，6），点B的坐标为（﹣，5），将△AOB沿x轴向左平移得到△A′O′B′，点A的对应点A′落在直线y＝﹣x上，则点B的对应点B′的坐标为（ ）





A．（﹣8，6）B．（﹣，5）C．（﹣，5）D．（﹣8，5）


9．“龟兔赛跑”是同学们熟悉的寓言故事．如图所示，表示了寓言中的龟、兔的路程S和时间t的关系（其中直线段表示乌龟，折线段表示兔子）．下列判断中，正确的是（ ）





A．赛跑中，兔子共休息了50分钟


B．兔子在不休息的时间段，速度都比乌龟快


C．乌龟追上兔子用了10分钟


D．兔子全程的平均速度大于10米/分


10．函数y＝kx与y＝﹣kx+k的大致图象是（ ）


A．B．C．D．


11．若点A（m，n）在一次函数y＝3x+b的图象上，且3m﹣n＞2，则b的取值范围为（ ）


A．b＜﹣2B．b＞﹣2C．b＜2D．b＞2


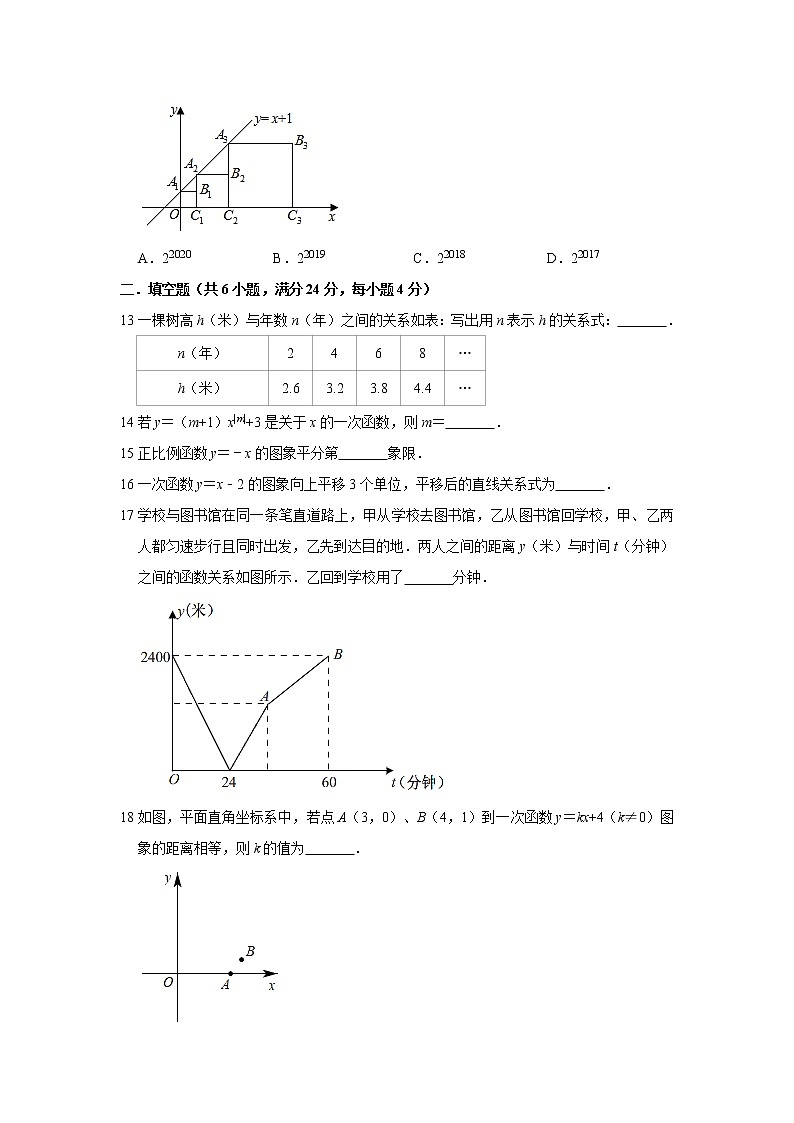
12．正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…按如图的方式放置，点A1，A2，A3，…和点C1，C2，C3，…分别在直线y＝x+1和x轴上，则点B2020的纵坐标是（ ）





A．22020B．22019C．22018D．22017


二．填空题（共6小题，满分24分，每小题4分）


13一棵树高h（米）与年数n（年）之间的关系如表：写出用n表示h的关系式： ．


14若y＝（m+1）x|m|+3是关于x的一次函数，则m＝ ．


15正比例函数y＝﹣x的图象平分第 象限．


16一次函数y＝x﹣2的图象向上平移3个单位，平移后的直线关系式为 ．


17学校与图书馆在同一条笔直道路上，甲从学校去图书馆，乙从图书馆回学校，甲、乙两人都匀速步行且同时出发，乙先到达目的地．两人之间的距离y（米）与时间t（分钟）之间的函数关系如图所示．乙回到学校用了 分钟．





18如图，平面直角坐标系中，若点A（3，0）、B（4，1）到一次函数y＝kx+4（k≠0）图象的距离相等，则k的值为 ．





三．解答题（共6小题）


19．在弹性限度内，弹簧的长度y（cm）是所挂物体质量x（kg）的一次函数．某弹簧不挂物体时长14.5cm；当所挂物体的质量为3kg时，弹簧长16cm．写出y与x之间的关系式，并求出所挂物体的质量为4kg时弹簧的长度．

















20．已知直线l1：y＝kx+b经过点A和点B（2，5）．


（1）求直线l1的解析式；


（2）若点C（a，a+2）与点D在直线l1上，过点D的直线l2与x轴正半轴交于点E，当AC＝CD＝CE时，求DE的长．














21．福州电信公司开设了A、B两种市内移动通信业务：A种使用者每月需缴18元月租费，然后每通话1分钟，再付话费0.1元：B种使用者不缴月租费，每通话I分钟，付话费0.3元若一个月内通话时间为x分钟，A、B两种的费用分别为y1和y2元．


（1）试分别写出y1、y2与x之间的函数关系式；


（2）每月通话时间为多长时，开通A种业务和B种业务费用一样．























22．已知函数y＝a﹣b|x﹣1|（a、b为常数），当x＝1时，y＝1；当x＝2时，y＝0；请对该函数及其图象进行如下探究：


（1）求函数的解析式；


（2）请在给出的平面直角坐标系中画出该函数的图象，并结合图象写出该函数的一条性质： ；


根据函数图象解决下列问题：


①若A（m，c），B（n，c）为该函数图象上不同的两点，则m+n＝ ；


②若方程a﹣b|x﹣1|＝x+k有两个不相等的实数解x1，x2，且x1•x2＞0，则k的取值范围是 ．











23．暑假期间，小刚一家乘车去离家380公里的某景区旅游，他们离家的距离y（km）与汽车行驶时间x（h）之间的三段函数图象如图．


（1）三段图象中，小刚行驶的速度最慢的是多少？


（2）求线段AB对应的函数表达式；


（3）小刚一家出发2.5小时时离目的地多远？








24．如图，平面直角坐标系中，直线y＝﹣x+与坐标轴交与点A、B．点C在x轴的负半轴上，且AB：AC＝1：2．


（1）求A、C两点的坐标；


（2）若点M从点C出发，以每秒1个单位的速度沿射线CB运动，连接AM，设△ABM的面积为S，点M的运动时间为t，写出S关于t的函数关系式，并写出自变量的取值范围；


（3）点P是y轴上的点，在坐标平面内是否存在点Q，使以A、B、P、Q为顶点，且以AB为边的四边形是菱形，若存在，请直接写出点Q的坐标；若不存在，请说明理由．



























































参考答案


一．选择题（共12小题，满分36分，每小题3分）


1．解：在圆周长的计算公式C＝2πr中，变量有C和r，


故选：B．


2．解：由题意得，x+3＞0，


解得，x＞﹣3，


故选：D．


3．解：当x＝0时，y＝2x+3＝3，


∴点M的坐标为（0，3）．


故选：D．


4．解：A、从表格可知：t＝0时，y＝10，即没有加热时，油的温度为10℃，选项正确，不符合题意；


B、每增加10秒，温度上升20℃，则50秒时，油温度110℃，选项正确，不符合题意；


C、110秒时，温度230℃，选项正确，不符合题意；


D、每增加10秒，温度上升20℃，选项错误，符合题意；


故选：D．


5．解：∵k＝5＞0，


∴y随x的增大而增大，


∴当x1＜x2时，y1＜y2．


故选：D．


6．解：根据题意，得：m﹣3＜0，


解得：m＜3，


故选：A．


7．解：在直线y＝﹣2x+6中，


当x＝0时，y＝6；


当y＝0时，x＝3；


∴直线y＝﹣2x+6与坐标轴交于（0，6），（3，0）两点，


∴直线y＝﹣2x+6与两坐标轴围成的三角形面积＝×6×3＝9．


故选：C．


8．解：由题意可知，点A移动到点A′位置时，纵坐标不变，


∴点A′的纵坐标为6，


∵点A′落在直线上y＝﹣x上，


∴﹣x＝6，解得x＝﹣8，


∴△OAB沿x轴向左平移得到△O′A′B′位置，移动了8个单位，


∴点B与其对应点B′的坐标为（﹣，5），


故选：C．


9．解：由图象可得，


赛跑中，兔子共休息了50﹣10＝40分钟，故选项A错误；


乌龟在这次比赛中的平均速度是500÷50＝10米/分钟，


兔子开始的速度是200÷10＝20米/分钟，后来的速度是500÷（60﹣50）＝50米/分钟，


即兔子在不休息的时间段，速度都比乌龟快，故选项B正确；


乌龟追上兔子用了20分钟，故选项C错误；


兔子全程的平均速度是500÷60＝米/分钟，故选项D错误；


故选：B．


10．解：A、由y＝kx的图象知k＞0，则﹣k＜0，所以y＝﹣kx+k的图象经过第一、二、四象限，故本选项不符合题意．


B、由y＝kx的图象知k＞0，则﹣k＜0，所以y＝﹣kx+k的图象经过第一、二、四象限，故本选项不符合题意．


C、由y＝kx的图象知k＜0，则﹣k＞0，所以y＝﹣kx+k的图象经过第一、三、四象限，故本选项不符合题意．


D、由y＝kx的图象知k＞0，则﹣k＜0，所以y＝﹣kx+k的图象经过第一、二、四象限，故本选项符合题意．


故选：D．


11．解：∵点A（m，n）在一次函数y＝3x+b的图象上，


∴3m+b＝n．


∵3m﹣n＞2，


∴﹣b＞2，即b＜﹣2．


故选：A．


12．解：∵直线y＝x+1，当x＝0时，y＝1，当y＝0时，x＝﹣1，


∴∠ODA1＝45°，即B1 的纵坐标是1，


∴∠A2A1B1＝45°，


∴A2B1＝A1B1＝1，


∴A2C1＝2＝21，即B2的纵坐标是2，


同理得：A3C2＝4＝22，即B3 的纵坐标是22，…，


∴点B2020的纵坐标是22019；


故选：B．


二．填空题（共6小题，满分24分，每小题4分）


13．解：设该函数的解析式为h＝kn+b，将n＝2，h＝2.6以及n＝4，h＝3.2代入后可得：


，


解得，


∴h＝0.3n+2，


验证：将n＝6，h＝3.8代入所求的函数式中，可得：等式左边＝3.8，右边＝0.3×6+2＝3.8，左边＝右边，


因此这个函数解析式为h＝0.3n+2，


故答案为：h＝2+0.3n．


14．解：由题意得：|m|＝1且m+1≠0，


解得：m＝1，


故答案为：1．


15．解：∵k＝﹣1＜0，


∴一次函数y＝﹣x的图象经过第二、四象限，且平分第二、四象限．


故答案是：二、四．


16．解：由题意得：平移后的解析式为：y＝x﹣2+3，即y＝x+1．


故答案为：y＝x+1．


17．解：由图象可得，


甲的速度为：2400÷60＝40（米/分钟），


乙的速度为：2400÷24﹣40＝60（米/分钟），


则乙回到学校用了：2400÷60＝40（分钟），


故答案为：40．


18．解：一次函数y＝kx+4（k≠0）图象一定过（0，4）点，


①当直线y＝kx+4（k≠0）与直线AB平行时，如图1，


设直线AB的关系式为y＝kx+b，


把A（3，0），B（4，1）代入得，


，解得，k＝1，b＝﹣3，


∴一次函数y＝kx+4（k≠0）中的k＝1，


②当直线y＝kx+4（k≠0）与直线AB不平行时，如图2，


则：直线y＝kx+4（k≠0）一定过点C，点C的坐标为（4，0），代入得，


4k+4＝0，解得，k＝﹣1，


因此，k＝1或k＝﹣1．


故答案为：k＝±1．








三．解答题（共6小题）


19．解：设y与x的函数关系式为y＝kx+b，由题意，得


，


解得：．


故y与x之间的关系式为：y＝0.5x+14.5；


当x＝4时，


y＝0.5×4+14.5＝16.5．


答：当所挂物体的质量为4kg时弹簧的长度为16.5cm．


20．解：（1）∵直线l1：y＝kx+b 经过A和点B（2，5）．


∴，解得，


即y＝2x+1，


当x＝0时，y＝2×0+1＝1，


即直线l1与y轴的交点坐标是（0，1）；





（2）解：如图，把C（a，a+2）代入y＝2x+1，可得a＝1，则点C的坐标为（1，3），


∵AC＝CD＝CE，


又∵点D在直线AC上，


∴点E在以线段AD为直径的圆上，


∴∠DEA＝90°，


过点C作CF⊥x轴于点F，


则 CF＝yC＝3，


∵AC＝CE，


∴AF＝EF，


又∵AC＝CD，


∴CF是△DEA的中位线，


∴DE＝2CF＝6．





21．解：（1）由题意可得，


y1＝0.1x+18（x⩾0），


y2＝0.3x（x⩾0）；





（2）令0.1x+18＝0.3x，


解得：x＝90，


答：每月通话时间为90分钟时，开通A种业务和B种业务费用一样．


22．解：（1）把x＝1时，y＝1；x＝2时，y＝0代入y＝a﹣b|x﹣1|得，


解得，


∴该函数的解析式为y＝1﹣|x﹣1|；


（2）如图：


描点连线：





观察图象可知：当x＞1时，y随x的增大而减小；当x＜1时，y随x的增大而增大；


故答案为当x＞1时，y随x的增大而减小；当x＜1时，y随x的增大而增大；


①由表格中数据可知：若A（m，c），B（n，c）为该函数图象上不同的两点，则m+n＝2；


故答案为2；


②把（1，1）代入y＝x+k得k＝；


根据题意结合函数y＝1﹣|x﹣1|的图象可知k的取值范围是0＜k＜，


故答案为0＜k＜．


23．解：（1）OA段小刚行驶的速度为：80÷1＝80（km/h），


AB段小刚行驶的速度为：（320﹣80）÷2＝120（km/h），


BC段小刚行驶的速度为：（380﹣320）÷1＝60（km/h），


∴BC段小刚行驶的速度最慢，为60（km/h）．





（2）设AB段图象的函数表达式为y＝kx+b．


∵A（1，80），B（3，320）在AB上，


∴，解得，


∴y＝120x﹣40（1≤x≤3）．





（3）当x＝2.5时，


y＝120×2.5﹣40＝260，


380﹣260＝120（km）．


故小刚一家出发2.5小时时离目的地120km远．





24．解：（1）对于直线y＝﹣x+，


当y＝0 时，﹣＝0，


解得：x＝1，


∴A（1，0），


∴OA＝1，


当x＝0 时，y＝，


∴B（0，），


∴OB＝，


∵∠AOB＝90°，


∴AB＝＝＝2，


∵AB：AC＝1：2，


∴AC＝4，


∴OC＝3，


∴C（﹣3，0）；





（2）如图所示，∵OA＝1，OB＝，AB＝2，





∴∠ABO＝30°，


同理：BC＝2，∠OCB＝30°，


∴∠OBC＝60°，


∴∠ABC＝90°，


分两种情况考虑：


①若M在线段BC上时，


BC＝2，CM＝t，可得BM＝BC﹣CM＝2﹣t，


此时S△ABM＝BM•AB＝×（2﹣t）×2＝2﹣t（0≤t＜2）；


②若M在BC延长线上时，BC＝2，CM＝t，


可得BM＝CM﹣BC＝t﹣2，


此时S△ABM＝BM•AB＝×（t﹣2）×2＝t﹣2（t≥2）；


综上所述，S＝；





（3）存在．


若AB是菱形的边，如图2所示，





在菱形AP1Q1B中，Q1O＝AO＝1，所以Q1点的坐标为（﹣1，0），


在菱形ABP2Q2中，AQ2＝AB＝2，所以Q2点的坐标为（1，2），


在菱形ABP3Q3中，AQ3＝AB＝2，所以Q3点的坐标为（1，﹣2），


综上，满足题意的点Q的坐标为（1，2）或（1，﹣2）或（﹣1，0）．





时间t/s
0
10
20
30
40
油温y/℃
10
30
50
70
90
n（年）
2
4
6
8
…
h（米）
2.6
3.2
3.8
4.4
…
x
…
﹣5
﹣4
﹣3
﹣2
﹣1
0
1
2
3
4
5
6
7
……
y
…
﹣5
﹣4
﹣3
﹣2
﹣1
0
1
0
﹣1
﹣2
﹣3
﹣4
﹣5
……