专题01 空间向量与立体几何(解答题热点，八大题型)-高考数学二轮热点题型归纳与变式演练（上海专用）

这是一份专题01 空间向量与立体几何(解答题热点，八大题型)-高考数学二轮热点题型归纳与变式演练（上海专用），文件包含专题01空间向量与立体几何原卷版docx、专题01空间向量与立体几何解析版docx等2份试卷配套教学资源，其中试卷共71页， 欢迎下载使用。

TOC \ "1-1" \h \u \l "_Tc27194" 题型01 直接求线面角2
\l "_Tc22731" 题型02 根据条件求线面角8
\l "_Tc394" 题型03 根据条件求线线角14
\l "_Tc1766" 题型04 直接求二面角16
\l "_Tc8506" 题型05 根据条件求面面角20
\l "_Tc6010" 题型06 空间中的距离问题32
\l "_Tc22452" 题型07 存在性问题34
\l "_Tc5641" 题型08 其他问题39
【解题规律·提分快招】
题型01 直接求线面角
【典例1-1】．（2024·上海·三模）如图，在四棱锥中，平面平面，，，，，，，点是的中点．

(1)求证：；
(2)求直线与平面所成角的正弦值．
【答案】(1)证明见解析
(2)
【分析】（1）利用面面垂直的性质可得平面，即得；
（2）根据（1）的结论，利用题设建系，依次写出各相关点的坐标，求出平面的一个法向量，利用空间向量夹角的坐标公式计算即得.
【解析】（1）因，点是的中点，则,
因平面平面，且平面平面, 平面，故平面，
又平面,故.
（2）

如图，取中点,连接，由（1）知平面，，可得,
因，故,则可分别以为轴正方向建立空间直角坐标系.
又，，，，则,
于是，,
设平面的一个法向量为，则，故可取，
设直线与平面所成角为，则，
即直线与平面所成角的正弦值为.
【典例1-2】．（2022·上海·模拟预测）如图所示三棱锥P-ABC，底面为等边三角形ABC，O为AC边中点，且底面ABC，

(1)求三棱锥P-ABC的体积；
(2)若M为BC中点，求PM与平面PAC所成角大小（结果用反三角数值表示）.
【答案】(1)1；
(2)．
【分析】（1）由棱锥体积公式计算；
（2）建立空间直角坐标系，用空间向量法二面角．
【解析】（1）底面ABC，底面ABC，则，连接，同理，
又，，∴，
而，
所以；
（2）由已知，分别以为轴建立空间直角坐标系，如图，
由已知，
则，，，∴，
，易知平面的一个法向量是，
，
设PM与平面PAC所成角大小为，则，，∴．

【变式1-1】．（2024·上海徐汇·二模）如图，为圆锥的顶点，是圆锥底面圆的圆心，为圆的直径，且，是底面圆的内接正三角形，为线段上一点，且.
(1)证明：平面；
(2)求直线与平面所成角的正弦值.
【答案】(1)证明见解析
(2)
【分析】（1）由勾股定理可得，，由此即可证明；
（2）方法一：建立空间直角坐标系，求解以及平面的法向量为，利用向量的坐标运算得线面夹角即可；方法二：利用体积相等求解点到平面的距离，即可得与平面所成角．
【解析】（1）证明：由题意得，，
，，
，
在中，由，得，
同理可得，又平面，故平面.
（2）（方法一）如图所示，以为坐标原点，、为轴正方向建立空间直角坐标系，
则点，故，，，
设平面的法向量为，
则，令，可得，
设直线与平面所成角为，
故，
因此直线与平面所成角的正弦值.
（方法二），，
则，．
记点到平面的距离为，因为，
所以，则，
设直线与平面所成角为，，
因此，直线与平面所成角的正弦值为．
【变式1-2】．（2023·上海普陀·三模）如图，在四棱锥中，正方形的边长为2，平面平面，且，，点分别是线段的中点.

(1)求证：直线平面；
(2)求直线与平面所成角的大小.
【答案】(1)证明见解析
(2)
【分析】（1）连接可得为的中位线，再利用线面平行的判定定理即可得出证明；
（2）利用四棱锥的结构特征以及线面垂直的判定定理，建立以为坐标原点的空间直角坐标系，利用空间向量和线面角的位置关系，即可求得直线与平面所成角的大小为.
【解析】（1）根据题意可知，连接，则交与；如下图所示：

在中，为的中点，又点是线段的中点，
所以，
又平面，平面，
所以直线平面；
（2）由平面平面，且平面平面，
又四边形是正方形，所以，又平面，
所以平面；
过点作直线平行于，又，
所以以为坐标原点，分别以直线，直线，直线为轴建立空间直角坐标系；如下图所示：

由正方形的边长为2，，可得，；
所以；
；
又点分别是线段的中点，所以；
即；
设平面的一个法向量为；
所以，可得，令，解得；
即
设直线与平面所成的角为，则
，解得；
所以直线与平面所成角的大小为.
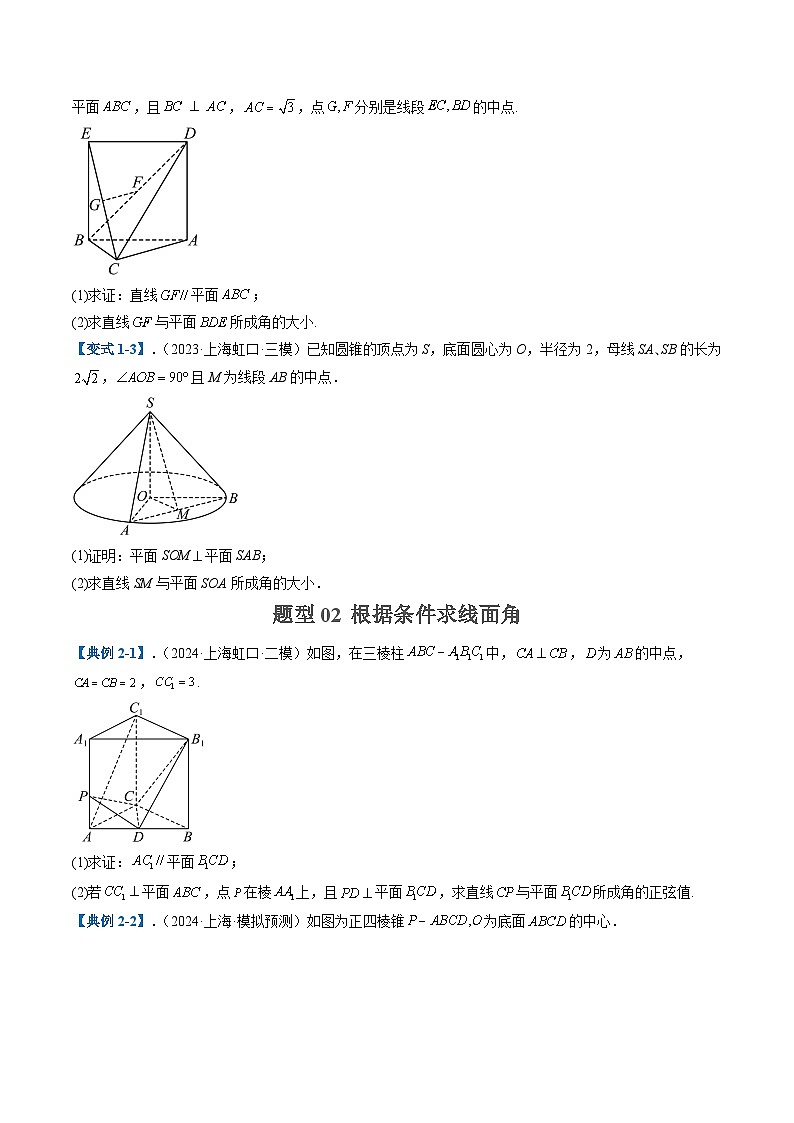
【变式1-3】．（2023·上海虹口·三模）已知圆锥的顶点为S，底面圆心为O，半径为2，母线SA､SB的长为，且M为线段AB的中点．

(1)证明：平面SOM平面SAB；
(2)求直线SM与平面SOA所成角的大小．
【答案】(1)证明见解析
(2)
【分析】（1）根据线面垂直判定定理证明线面垂直再由面面垂直判定定理证明即可；
（2）由线面角定义求线面角求正切再求角即可.
【解析】（1）因为为中点，所以，
因为平面，平面，
所以，且，平面，平面，
所以平面，
又因为平面，所以平面平面．
（2）
设的中点为，连接，则，
因为，所以，
因为底面，所以,平面，平面，,
所以平面，
所以即是直线与平面所成角．
因为圆锥的底面半径为2，母线长为，所以高，
得．
因为，
所以，
所以．
题型02 根据条件求线面角
【典例2-1】．（2024·上海虹口·二模）如图，在三棱柱中，，为的中点，，.
(1)求证：平面；
(2)若平面，点在棱上，且平面，求直线与平面所成角的正弦值.
【答案】(1)证明见解析
(2)
【分析】（1）连接，交于点，连接，即可得到，从而得证；
（2）建立空间直角坐标系，设点的坐标为，由平面，则即可求出，从而确定点坐标，再由空间向量法计算可得.
【解析】（1）连接，交于点，连接，
为的中点，在平行四边形中为的中点，
是的中位线，可得，
平面，平面，
平面；
（2）因为平面，平面，所以，，又，
故以点C为坐标原点，直线分别为轴，建立空间直角坐标系，
则
设点的坐标为，则，，
因为平面，平面，所以，
所以，解得，经检验符合题意.
所以 ，则，
又，，
设平面的一个法向量为，
则，即，取得，
设直线与平面所成的角为，
则，
故直线与平面所成角的正弦值为.
【典例2-2】．（2024·上海·模拟预测）如图为正四棱锥为底面的中心．
(1)若，求绕旋转一周形成的几何体的体积；
(2)若为的中点，求直线与平面所成角的大小．
【答案】(1)
(2)
【分析】（1）根据正四棱锥的数据，先算出直角三角形的边长，然后求圆锥的体积；
（2）连接，可先证平面，根据线面角的定义得出所求角为，然后结合题目数量关系求解.
【解析】（1）正四棱锥满足且平面，由平面，则，
又正四棱锥底面是正方形，由可得，，
故，
根据圆锥的定义，绕旋转一周形成的几何体是以为轴，为底面半径的圆锥，
即圆锥的高为，底面半径为，
根据圆锥的体积公式，所得圆锥的体积是
（2）连接，由题意结合正四棱锥的性质可知，每个侧面都是等边三角形，
由是中点，则，又平面，
故平面，即平面，又平面，
于是直线与平面所成角的大小即为，
不妨设，则，，
又线面角的范围是，
故.即为所求.
【变式2-1】．（2024·上海奉贤·三模）如图，四棱锥的底面是梯形，，，，平面，．
(1)求证：平面
(2)若二面角的大小为，求与平面所成的角的大小．（结果用反三角函数值表示）
【答案】(1)证明见解析；
(2).
【分析】（1）利用线面垂直的性质、判定推理即得.
（2）由已知及（1）确定二面角的平面角及线面角，再结合数量关系求出线面角的正切.
【解析】（1）在四棱锥中，连接，由平面，平面，
得，而，平面，
所以平面.
（2）在梯形中，由，，得，又，
则，由（1）知，平面，平面，得，
则，是与平面所成的角，是二面角的平面角，
即，在中，，于是，
因此，所以与平面所成角的大小为.
【变式2-2】．（2024高三下·上海·专题练习）如图，在圆柱中，底面直径等于母线，点在底面的圆周上，且，是垂足．
(1)求证：；
(2)若圆柱与三棱锥的体积的比等于，求直线与平面所成角的大小．
【答案】(1)证明见解析
(2)
【分析】（1）根据题意，证得平面，得到，结合，证得平面，进而证得；
（2）过点作，证得平面，得到是与平面所成的角，设圆柱的底面半径为，求得，进而求得的值．
【解析】（1）证明：根据圆柱性质，平面，
因为平面，所以，
又因为是圆柱底面的直径，点在圆周上，所以，
因为且平面，所以平面，
又因为平面，所以，
因为，且，且平面，所以平面，
又因为平面，所以．
（2）解：过点作，是垂足，连接，
根据圆柱性质，平面平面，且平面平面,
且平面，所以平面，
因为平面，所以是在平面上的射影，
从而是与平面所成的角，
设圆柱的底面半径为，则，
所以圆柱的体积为，且，
由，可得，可知是圆柱底面的圆心，且，
且，
在直角中，可得，所以．
【变式2-3】．（2024·上海·模拟预测）如图，多面体是由一个正四棱锥与一个三棱锥拼接而成，正四棱锥的所有棱长均为，且．
(1)在棱上找一点，使得平面平面，并给出证明；
(2)若，求直线与平面所成角的正弦值．
【答案】(1)点为的中点，证明见解析
(2)
【分析】（1）当点为中点时，平面平面，依题意可得，从而得到，再由，即可证明平面，从而得证；
（2）建立合适的空间直角坐标系，利用线面角的空间向量求法即可.
【解析】（1）当点为中点时，平面平面，
证明如下：因为四棱锥是正四棱锥，所以，所以.
在正方形中，，所以，
在正方形中，，因为，所以，
因为面，
所以平面，
因为平面，所以平面平面.
（2）因为四棱锥是正四棱锥且所有棱长均为，设，
则，，两两垂直，
以为坐标原点，建立如图所示的空间直角坐标系，
则，则，
设，则，因为，，
所以，则，解得，所以，
所以，
设平面的法向量为，则有，
取，则，故，
设直线与平面所成角为，
则，
所以直线与平面所成角的正弦值为.
题型03 根据条件求线线角
【典例3-1】．（2024高三·上海·专题练习）如图，在四棱锥中，已知底面为矩形，侧面是正三角形，侧面底面是棱的中点，.
(1)证明：平面；
(2)若二面角为，求异面直线与所成角的正切值.
【答案】(1)证明见解析
(2)
【分析】（1）利用面面垂直的性质，线面垂直的性质 判定推理即得.
（2）作出二面角的平面角，由此求出，再利用异面直线所成角的定义求出其正切值.
【解析】（1）在四棱锥中，由底面为矩形，得，
由侧面底面，侧面底面平面，
得平面，又平面，则，
又侧面是正三角形，是的中点，则，
又平面，所以平面.
（2）如图，
在平面内，过点作，垂足为，显然，
由侧面底面，交线为，得底面，底面，
则，过作，垂足为，连接，显然，
平面，则平面，而平面，因此，
则即为二面角的平面角，其大小为，
在中，，则，
由，得四边形为平行四边形，则，
由，得（或其补角）为异面直线与所成角，
由（1）知平面，则为直角三角形，，
所以异面直线与所成角的正切值为.
【变式3-1】．（2024·上海宝山·二模）如图，已知点在圆柱的底面圆的圆周上，AB为圆的直径.
(1)求证：；
(2)若，，圆柱的体积为，求异面直线与所成角的大小.
【答案】(1)证明见解析
(2)
【分析】（1）通过证明平面，即可求解；
（2）延长交圆于点，连接、、，易知(或其补角即为所求的角，即可求解.
【解析】（1）证明：易知，
又由平面，平面，得，
而平面，
则平面，而平面，故.
（2）延长交圆于点，连接、、，
易知(或其补角即为所求的角，
由题知，解得，
中，
由余弦定理得，
所以，所以异面直线与所成角的大小为.
题型04 直接求二面角
【典例4-1】．（2024·上海·一模）三棱柱中，平面，且，为中点．

(1)求四面体的体积：
(2)求平面与所成锐二面角的余弦值．
【答案】(1)
(2)
【分析】（1）利用等体积法，再根据条件，即可求出结果；
（2）建立空间直角坐标系，求出平面与的法向量，再利用面面角的向量法，即可求出结果.
【解析】（1）因为平面，又面，所以，
又，，面，所以面，
因为面，所以到面的距离即,
又，，
所以.
（2）如图，建立空间直角坐标系，因为，，
则，
所以
设平面的一个法向量为，
由，得到，取，得到，所以，
设平面的一个法向量为，
则由，得到，取，则，所以，
设平面与所成锐二面角为，
则.

【变式4-1】．（2024·上海金山·二模）如图，几何体是圆柱的一部分，它是由矩形（及其内部）以边所在直线为旋转轴旋转得到的，点是的中点，点在上，异面直线与所成的角是．

(1)求证：；
(2)若，，求二面角的大小．
【答案】(1)证明见解析
(2)
【分析】（1）由题意易得，结合，可证平面，进而可证结论；
（2）法一：取的中点，连接，，，取中点，连接，，，可得为所求二面角的平面角，进而求解可得二面角E−AG−C的大小．
法二：以为坐标原点，分别以、、的方向为、、轴的正方向，建立空间直角坐标系，求得平面的一个法向量和平面的一个法向量，利用向量的夹角公式可求得二面角E−AG−C的大小．
【解析】（1）因为，所以是直线与所成角，为，
所以，得，
又因为，且，平面，平面，
所以平面，
由平面，得．
（2）解法一：取的中点，连接，，．
因为，
所以四边形为菱形，
所以．
取中点，连接，，．

则，，
所以为所求二面角的平面角．
又，所以．
在中，由于，
由余弦定理得，
所以，因此为等边三角形，
因此二面角E−AG−C的大小为．
解法二：以为坐标原点，分别以、、的方向为、、轴的正方向，建立如图所示的空间直角坐标系．
由题意得，，，，

故，，，
设是平面的一个法向量．
由，可得，
取，可得平面的一个法向量．
设是平面的一个法向量．
由，可得，
取，可得平面的一个法向量．
所以．
因此二面角E−AG−C的大小为．
题型05 根据条件求二面角
【典例5-1】．（2024·上海·模拟预测）如图，、、为圆锥三条母线，.
(1)证明:；
(2)若圆锥侧面积为为底面直径，，求二面角的大小
【答案】(1)证明见解析
(2)
【分析】（1）取中点，连接、，则，故可得面，从而得到.
（2）利用向量法可求面、面的法向量，计算出它们的夹角的余弦值后可得二面角的余弦值.
【解析】（1）取中点，连接、，
因为，所以，
又因为面面，所以面，
因为面，所以.
（2）因为为直径，故为底面圆的圆心，故平面，而
故可建立如图所示的空间直角坐标系，
因为圆锥侧面积为为底面直径，，所以底面半径为1，母线长为3，
所以，
则可得，
故，
设为平面的法向量，则，
令，则，所以.
设为平面的法向量，
则，
令，则，所以.
则，
设二面角为，则为钝角，
所以二面角的大小为.
【典例5-2】．（2024·上海·三模）如图，在三棱锥中，，，点O是AC的中点．
(1)证明：平面ABC；
(2)点M在棱BC上，且，求二面角的大小．
【答案】(1)证明见解析
(2)．
【分析】（1）根据等腰和等边三角形的性质证明以及，然后利用线面垂直的判断证明平面ABC
（2）建立空间直角坐标系，利用空间向量求角公式求解即可
【解析】（1）连结OB，，，所以，
所以是等腰直角三角形，又点O是AC的中点，所以，
由已知可得，是等边三角形，所以，
又，所以，所以，
中，，O是AC的中点，所以，
，，，且平面ABC，平面ABC，
所以平面ABC．
（2）OB，OC，OP两两垂直，以、、为x轴、y轴、z轴正方向建立空间直角坐标系
则，，，，
由，即
所以点
则，，
设平面APM的—个法向量为，
则，令，
平面PAC的一个法向量，
，
所求二面角的平面角是锐角，所以二面角为的大小为．
【变式5-1】．（2024高三·上海·专题练习）如图，在三棱柱中，平面平面，，四边形是边长为2的正方形.
(1)证明：平面；
(2)若直线与平面所成的角为30°，求二面角的余弦值．
【答案】(1)证明见解析
(2)
【分析】（1）先证明平面，从而得到，进而即可证明平面；
（2）结合（1）及题意可得为直线与平面所成的角，即，从而得到，，．（方法一）过点作，垂足为，过点作，垂足为，连结，先证明，平面，再平面，从而证明，从而可得是二面角的平面角，进而即可求出二面角的余弦值；（方法二）取的中点，连结，先证明平面，再取的中点，以为基底，建立空间直角坐标系，再根据向量夹角公式即可求解．
【解析】（1）因为四边形是正方形，所以，
又平面平面，平面，平面平面，所以平面，
因为平面，所以，
又因为，，平面，，
所以平面．
（2）由（1）知，为直线与平面所成的角，即，
又正方形的边长为2，所以，，所以，
（方法一）过点作，垂足为，过点作，垂足为，连结，
因为平面，平面，所以，
又，平面，，所以平面，
又平面，则，
又，平面，，所以平面，
又平面，所以，
所以是二面角的平面角，
在直角中，，，
所以，所以，
即二面角的余弦值为．
（方法二）取的中点，连结，
因为，所以，
又因为平面平面，平面平面，平面，所以平面，
取的中点，则，
以为基底，建立空间直角坐标系，
所以B1,0,0，，，
所以，，
设平面的法向量为n=x,y,z，
则，即，取，则，
取平面的法向量，
设二面角的大小为，
则，
因为二面角为锐角，所以，
即二面角的余弦值为．
【变式5-2】．（2024高三·上海·专题练习）小红同学利用计算机动画演示圆柱的形成过程，将正方形绕直线逆时针旋转弧度时，到达的位置，得到如图所示的几何体.
(1)求证：平面平面；
(2)若是的中点，求二面角的正弦值.
【答案】(1)证明见解析
(2)
【分析】（1）由已知可证平面，可证，根据，可证平面，可证结论；
（2）以为坐标原点，所在直线分别为轴建立空间直角系，求得平面的一个法向量，平面的一个法向量，利用向量法可求二面角的余弦值，进而可求结论.
【解析】（1）平面，
平面，平面，，
是正方形，.
又平面，
平面，
又平面平面平面.
（2）由（1）知：两两垂直，以为坐标原点，所在直线分别为轴建立空间直角坐标系如图所示.
，不妨设，
则，
，
设是平面的一个法向量，
则，取得.
同理可得平面的一个法向量为n=1,-1,1.
，
即二面角的余弦值的绝对值为
二面角的正弦值为.
【变式5-3】．（2023·上海浦东新·模拟预测）如图，直三棱柱内接于圆柱，，平面平面
(1)证明：是圆柱下底面的直径；
(2)若为中点，为中点，求平面与平面所成二面角的正弦值.
【答案】(1)证明见解析
(2)
【分析】（1）连接，利用平面平面可得到平面，继而得到，结合可得到平面，所以，即可求证；
（2）以为正交基底建立空间直角坐标系，计算出平面和平面的法向量，然后用夹角公式进行求解即可
【解析】（1）连接，在直三棱柱中，，
四边形为正方形，，
又平面平面，平面平面平面，
平面，又平面
又平面平面，
又平面，
平面，又平面，
为圆柱底面的直径.
（2）由已知平面，
以为正交基底建立空间直角坐标系，
，
为中点，，
设平面的一个法向量为，
则，又，
，取，得，
设平面的一个法向量为，
则，又，
，取，得，
，
所以平面与平面所成二面角的余弦值为，对应的正弦值为
【变式5-4】．（2023·上海奉贤·一模）在《九章算术》中，将四个面都是直角三角形的四面体称为鳖臑．如图，已知四面体中，平面，．
(1)若，求证：四面体是鳖臑，并求该四面体的体积；
(2)若四面体是鳖臑，当时，求二面角的平面角的大小．
【答案】(1)证明见解析，
(2)或
【分析】（1）借助线面垂直证明面面垂直，结合题目所给长度，运用勾股定理证明四面全为直角三角形即可，体积借助体积公式计算即可得；
（2）根据题意，会出现两种情况，即或，分类讨论计算即可得.
【解析】（1）平面，、平面，
、，
、为直角三角形，
在直角中，，
在直角中，，
在中，有，
，故为直角三角形，
在中，有，
故，故为直角三角形，
故四面体四个面都是直角三角形，即四面体是鳖臑，
；
（2）平面，平面，
，
由，
故不可能是直角，
若，则有，
又，、平面，，
故平面，又平面，
故，
是二面角的平面角，
，，，，
所以二面角的平面角的大小为．
若，
同理可得是二面角的平面角，
所以，
所以二面角的平面角的大小为，
综上所述，二面角的平面角的大小为或.
【变式5-5】．（2024·上海黄浦·二模）如图，在四棱锥中，底面为矩形，点E是棱PD上的一点，平面.

(1)求证：点E是棱PD的中点；
(2)若平面，，，与平面ABCD所成角的正切值为，求二面角的大小.
【答案】(1)证明见解析
(2)
【分析】（1）作出辅助线，由线面平行得到线线平行，结合点是BD的中点，得到证明；
（2）方法一：作出辅助线，得到就是PC与平面ABCD所成角，从而根据正切值得到，证明出线面垂直，得到是二面角的平面角，求出各边长，从而得到；
方法二：作出辅助线，得到就是PC与平面ABCD所成角，建立空间直角坐标系，得到平面的法向量，利用法向量夹角余弦值得到二面角的大小.
【解析】（1）连接BD，它与AC交于点，连接EF，
四边形ABCD为矩形，
为BD的中点，
平面AEC，平面PBD经过PB且与平面AEC交于，
，
又点是BD的中点，
点是棱的中点.
（2）方法一：∵PA⊥平面，平面，
且就是PC与平面ABCD所成的角，
故，解得.
四边形ABCD为矩形，
，又，PA与AD是平面PAD内的两相交直线，
平面PAD.
在平面PAD内作，垂足为，连接GF，则，
是二面角的平面角.
在直角三角形PAD中，，点是PD的中点，
，且，
平面平面，
，故，所以，
故二面角的大小为.
方法二：∵PA⊥平面，平面，
且就是PC与平面ABCD所成的角，
又四边形ABCD为矩形，，
分别以AB，AD，AP为x，y，z轴，建立空间直角坐标系，

设是平面AEC的一个法向量，二面角的大小为，
由，可得，
则，
故，
解得且，所以，
又是平面AED的一个法向量，且为锐角，
故，可得.
所以二面角的大小为.
题型06 空间中的距离问题
【典例6-1】．（2023·上海崇明·一模）如图，四棱锥中，平面，，，，，E，F分别为的中点．
(1)求证：平面；
(2)求点B到平面的距离．
【答案】(1)证明见解析
(2)
【分析】（1）设是的中点，连接，，证明四边形是平行四边形，可得，再根据线面平行的判定定理即可得证；
（2）先证明，再利用等体积法求解即可.
【解析】（1）证明：取中点，连接、，
由于是的中点，则，，
由于，，所以，，
所以四边形是平行四边形，所以，
由于上，平面，
所以平面.
（2）设点到平面的距离为，
因为平面，平面，所以，
由于，，所以四边形是平行四边形，
由于，所以，
由于平面，
所以平面，
又平面，所以，
在中，，所以，又.
由得，
即，
所以，即点B到平面的距离为.
【变式6-1】．（2023·上海杨浦·一模）如图所示，在四棱锥中，平面，底面是正方形.

(1)求证：平面平面；
(2)设，若四棱锥的体积为，求点到平面的距离.
【答案】(1)证明见解析
(2)
【分析】（1）先证明线面垂直，再由面面垂直的判定定理得证；
（2）利用等体积法求解即可.
【解析】（1）因为平面，平面，
所以，
因为底面是正方形，所以，
又平面，
所以平面，又平面，
所以平面平面.
（2）因为四棱锥的体积为，
所以，解得，
又平面，所以，
所以，,
所以正三角形面积为，
设点到平面的距离为，
则由可得：，
即，解得.
即点到平面的距离为.
题型07 存在性问题
【典例7-1】．（2024·全国·模拟预测）如图，在多面体中，已知四边形是菱形，，平面，平面，.
(1)在线段上是否存在一点，使得平面平面？若存在，确定点的位置；若不存在，请说明理由.
(2)求二面角的余弦值.
【答案】(1)存在，为的中点
(2)
【分析】（1）设为的中点，连接，利用线面垂直可得，从而根据平行关系可证得平面，平面，再结合面面平行的判定定理即可证得结论；
（2）建立空间直角坐标系，分别求解平面与平面的法向量，再根据空间向量的坐标运算确定法向量夹角的余弦值，根据二面角的性质即可得结论.
【解析】（1）线段上存在一点，使得平面平面，且为的中点.理由如下：
如图，设为的中点，连接，
因为平面平面，所以，即，
又，所以，
所以四边形是平行四边形，所以，
因为平面，平面，所以平面；
又，，所以四边形是平行四边形，
所以，，
又，，所以，，
所以四边形是平行四边形，所以，
因为平面，平面，所以平面；
又，平面，
所以平面平面.
（2）连接，设与相交于点，
因为四边形是菱形，所以.
以为坐标原点，所在直线为轴，所在直线为轴，过点且与平行的直线为轴建立如图所示的空间直角坐标系，
则，，故，，，.
设是平面的法向量，
则，即，
取，则，故.
设是平面的法向量，
则，即，
故，取，则，故.
所以，
由图易知二面角是钝二面角，
所以二面角的余弦值为.
【典例7-2】．（2023·上海长宁·三模）已知和所在的平面互相垂直，，，，，是线段的中点，.
(1)求证：；
(2)设，在线段上是否存在点（异于点），使得二面角的大小为.
【答案】(1)证明见解析
(2)不存在，理由见解析
【分析】（1）根据余弦定理计算，根据勾股定理得到，确定平面，得到证明.
（2）建立空间直角坐标系，计算各点坐标，平面的一个法向量为，平面的一个法向量为，根据向量的夹角公式计算得到答案.
【解析】（1），故，
，则，故，
又，平面，，故平面，
平面，故，

（2）△和△所在的平面互相垂直，则平面平面，
且平面，故平面，
如图所示：以分别为轴建立空间直角坐标系，

则，，，设，，
平面的一个法向量为，
设平面的一个法向量为，则，
取得到，
则，解得，不满足题意.
综上所述：不存在点，使二面角的大小为.
【变式7-1】．（2024高三·上海·专题练习）如图，在四面体中，平面，点为中点，且，，.
(1)证明：；
(2)求平面与平面夹角的余弦值；
(3)在直线上是否存在点，使得直线与平面所成角的正弦值为？若存在；求的值；若不存在，请说明理由.
【答案】(1)证明见详解
(2)
(3)存在，
【分析】（1）由勾股定理得，由平面得，从而平面，进而得出结论；
（2）以A为坐标原点，以所在直线分别为轴，建立空间直角坐标系，求出平面与平面的法向量，利用向量夹角公式求解；
（3）设，则，求得，设直线与平面所成角为，由题意，列式求解即可.
【解析】（1）因为，则，即，
又因为平面，平面，则，
且，平面，
可得平面，
由平面，可得.
（2）以A为坐标原点，以所在直线分别为轴，建立空间直角坐标系，
则，
可得,
设平面的法向量为，则，
令，则，可得，
设平面的法向量为，则，
令，则，可得，
则，
所以平面和平面夹角的余弦值为.
（3）设，则，
设，则，得，
即，可得，
平面的法向量为，
设直线与平面所成角为，
由题意，，
整理可得，解得或（舍去），
所以存在，使得直线与平面所成角的正弦值为，此时.
题型08 其他问题
【典例8-1】．（2023·上海普陀·二模）如图，在直三棱柱中，，，．
(1)求证：；
(2)设与底面ABC所成角的大小为，求三棱锥的体积．
【答案】(1)证明见解析
(2)
【分析】（1）由证出，再由线面垂直的性质得出，
然后根据线面垂直的判定定理即可得证；
（2）由为与底面ABC所成角求出棱柱的高，再由等体积法求体积即可.
【解析】（1），，，
，
，
又直三棱柱中，平面，
平面，，
又，平面，
平面，
平面，.
（2）平面，
在平面上的射影为，即为与底面ABC所成角，
，，
.
【典例8-2】．（2023·上海闵行·二模）已知正方体，点为中点，直线交平面于点.

(1)证明：点为的中点；
(2)若点为棱上一点，且直线与平面所成角的正弦值为，求的值.
【答案】(1)证明见解析.
(2).
【解析】（1）在正方体中，，又平面，且平面，
则平面，而交平面于点，即平面，
又平面，有平面，因此平面平面，
于是，而为中点，
所以为的中点.
（2）以为坐标原点，方向分别为轴的正方向，建立空间直角坐标系，

不妨设正方体的棱长为3，设，
则,
从而，
设平面的一个法向量为，则
,即,不妨取,则,即，
设直线与平面所成角为，
又直线与平面所成角的正弦值为，
因此，解得，
所以.
【变式8-1】．（2023·上海普陀·一模）图1所示的是等腰梯形，，，，于点，现将沿直线DE折起到的位置，形成一个四棱锥，如图2所示.
(1)若，求证：平面；
(2)若直线与平面所成的角为，求二面角的大小.
【答案】(1)证明见解析
(2)
【分析】（1）连接，由，证得,再由，利用线面垂直的判定定理，即可证得平面；
（2）以为原点，建立空间直角坐标系，根据题意证得平面平面，过点作，证得平面，得到，分别求得平面和平面的法向量和，结合向量的夹角公式，即可求解.
【解析】（1）证明：如图所示，连接，
因为等腰梯形，，，，，
可得，且,即，
因为，则，所以,
又因为，且，平面，
所以平面.

（2）解：以为原点，以所在的直线分别为轴，以过点垂直于平面为轴，建立空间直角坐标系，如图所示，
因为，且，平面，
所以平面，
又因为平面，所以平面平面，
过点作于点，因为平面平面，
所以平面，所以为与平面所成的角，所以，
可得，则，
设平面的法向量为，则，
取，可得，所以，
又由轴垂直平面，可得平面的一个法向量为，
则，
所以二面角的大小.

【变式8-2】．（2023·上海嘉定·一模）中国历史悠久，积累了许多房屋建筑的经验．房梁为柱体，或取整根树干而制为圆柱形状，或作适当裁减而制为长方体形状，例如下图所示．
材质确定的梁的承重能力取决于截面形状，现代工程科学常用抗弯截面系数W来刻画梁的承重能力．对于两个截面积相同的梁，称W较大的梁的截面形状更好．三种不同截面形状的梁的抗弯截面系数公式，如下表所列，
(1)假设上表中的三种梁的截面面积相等，请问哪一种梁的截面形状最好？并具体说明；
(2)宋朝学者李诫在《营造法式》中提出了矩形截面的梁的截面长宽之比应定为的观点．考虑梁取材于圆柱形的树木，设矩形截面的外接圆的直径为常数D，如下图所示，请问为何值时，其抗弯截面系数取得最大值，并据此分析李诫的观点是否合理．
【答案】(1)矩形截面的梁的截面形状最好.
(2)答案见解析
【分析】（1）根据题意，得到，，，结合题意，得到，得到结论；
（2）根据题意，得到，得到，求得函数的单调性，求得时，取得最大值，进而得到结论.
【解析】（1）解：假设截面面积均为正常数，
可得，，，
所以，
又因为，所以，所以,
综上，，于是矩形截面的梁的截面形状最好.
（2）解：由，
可得，
可得
所以，当时，取得最大值，
此时，当，于是，
因为的结论与抗弯系数理论的结论不同，但比较接近，是合理的，应肯定李诫从实践总总结的经验的实用价值，
考虑到所处的时代，从历史辩证的角度，其观点代表了我国古代在工程技术方面已经达到了较高的水平.
一、解答题
1．（2023·上海·模拟预测）在直四棱柱中，，，，，
(1)求证：平面；
(2)若四棱柱体积为36，求二面角大小.
【答案】(1)证明见解析
(2)
【分析】（1）利用直四棱柱的性质及线面平行的判定定理，可证平面平面，再由面面平行的性质定理，即可得证；
（2）先根据棱柱的体积公式求得，再利用二面角的定义，求解即可．
【解析】（1）由题意知，，
因为平面，平面，
所以平面，
因为，且平面，平面，
所以平面，
又，、平面，
所以平面平面，
因为平面，
所以平面．
（2）由题意知，底面为直角梯形，
所以梯形的面积，
因为四棱柱的体积为36，
所以，
过作于，连接，
因为平面，且平面，
所以，
又，、平面，
所以平面，
因为平面，所以，
所以即为二面角的平面角，
在△中，，
所以，
所以，即，
故二面角的大小为．
2．（2024·上海杨浦·二模）如图，为圆锥顶点，为底面中心，，，均在底面圆周上，且为等边三角形.

(1)求证：平面平面；
(2)若圆锥底面半径为2，高为，求点到平面的距离.
【答案】(1)证明见解析
(2)
【分析】（1）连接，根据给定条件，利用线面垂直的性质判定、面面垂直的判定推理即得.
（2）连接，作于，证明平面，再计算即得.
【解析】（1）连接，交于点，由为等边三角形，得是的中心，则，
而平面，平面，则，又平面，
因此平面，又平面，
所以平面平面.

（2）连接，作于，由（1）知平面，平面，则，
而平面，则平面，
显然，，则，
而，于是≌，因此，
所以点到平面的距离为.
3．（2024·上海闵行·二模）如图，已知为等腰梯形， ，，平面，.
(1)求证：；
(2)求二面角的大小.
【答案】(1)证明见解析；
(2).
【分析】（1）连接，利用等腰梯形的性质证得，再利用线面垂直的性质判定推理即得.
（2）取的中点，作出二面角的平面角，在中求解即得.
【解析】（1）连接，在等腰梯形中，，，，
则，于是，即，
由平面，平面，得，
而平面，因此平面，又平面，
所以.
（2）取的中点，连接，由，得，
在中，，
由平面，平面，得，
则，于是，
因此为二面角的平面角，
因为，平面，
则平面，又平面，则，
在中，，，则，
所以二面角的大小为.
4．（2024·上海松江·二模）如图，在四棱锥中，底面为菱形，平面，为的中点.
(1)设平面与直线相交于点，求证：；
(2)若，，，求直线与平面所成角的大小.
【答案】(1)证明见解析
(2)
【分析】（1）根据线面平行的判定定理，证出平面，然后根据平面平面，利用线面平行的性质定理证出；
（2）连接，取中点，连接、，根据线面垂直的判定定理，证出平面，可得是直线与平面的所成角，然后在中利用锐角三角函数的定义算出答案．
【解析】（1）证明：平面与直线相交于点，平面平面，
四边形是菱形，，
平面，平面，平面，
平面，平面平面，
；
（2）连接，取中点，连接、，
菱形中，，，是等边三角形，
是中点，，
平面，平面，，
、平面，，平面．
是直线与平面的所成角，
是中点，，．
平面，平面，，
为中点，，中，，
等边中，高，
中，，
可得，即直线与平面的所成角等于．
5．（2024·上海嘉定·模拟预测）如图，在正四棱锥中，，E、F分别为PB、PD的中点，平面与棱PC的交点为G.
(1)求平面与平面所成锐二面角的大小；
(2)若，求的值.
【答案】(1)
(2)
【分析】（1）连接AC，BD，相交于点O，连接EF，与OP相交于点Q，依题意可得，从而得到平面，设平面与平面相交于直线l，根据线面平行的性质得到，连接QA，即可得到，又，则即为平面与平面所成锐二面角，再根据锐角三角函数的定义计算可得；
（2）延长AQ，则由两平面相交的性质可得AQ一定过点G，过点G作交AC于点M，依题意可得底面ABCD，设，则，根据，即可求出，最后根据计算可得.
【解析】（1）连接AC，BD，相交于点O，因为四边形ABCD是正方形，
所以O是正方形的中心，连接PO，因为四棱锥是正四棱锥，则底面ABCD，
连接EF，与OP相交于点Q，因为E、F分别为PB、PD的中点，
则Q为OP，EF的中点，EF是三角形PBD的中位线，所以，
因为平面ABCD，平面ABCD，所以平面ABCD，平面，
设平面AEGF与平面ABCD相交于直线l，故，连接QA，
则因为，所以，又因为，
因为，所以，，
故即为平面AEGF与平面ABCD所成锐二面角，其中，，所以，
即平面AEGF与平面ABCD所成锐二面角的大小为；
（2）延长AQ，因为平面平面，则由两平面相交的性质可得AQ一定过点G，
过点G作交AC于点M，因为底面ABCD，所以底面ABCD，
设，则，由（1）知，
所以，即，解得，故，所以，
所以.
6．（2023·上海宝山·一模）如图，在直三棱柱中，，，且分别是的中点.
(1)证明：；
(2)求三棱锥的体积；
(3)求直线与平面所成角的大小.（结果用反三角函数值表示）
【答案】(1)证明见解析
(2)
(3)
【分析】（1）结合题意先通过线线垂直得到面,进而得到；
（2）利用等体积法，转化为求的体积即可;
（3）利用上问求出点到面的距离为，借助线面角的定义即可求出线面角.
【解析】（1）证明：在直三棱柱中中，因为分别是的中点,所以,
由直三棱柱中面,
所以面，因为在面内，所以,
因为在中，，且是的中点,所以,
因为,且在面内，
所以面,因为在面内,所以.
（2）等腰中，，从而，
所以，
由面，且
所以，
又因为，
所以三棱锥的体积为.
（3）由（2），
令点到面的距离为，
则有，
中，，,
从而.
所以，
设直线与平面所成角为，则,
所以直线与平面所成角的大小为.
7．（2024·上海静安·二模）如图1所示，是水平放置的矩形，，．如图2所示，将沿矩形的对角线向上翻折，使得平面平面．
(1)求四面体的体积；
(2)试判断与证明以下两个问题：
① 在平面上是否存在经过点的直线，使得？
② 在平面上是否存在经过点的直线，使得？
【答案】(1)2；
(2)①证明见解析；②证明见解析.
【分析】（1）过点作，垂足为．可知为三棱锥的高，利用等面积法求得，再由棱锥体积公式求解；
（2）①过点作，垂足为，由直线与平面垂直的判定与性质证明；
②利用反证法证明在平面上不存在经过点的直线，使得．
【解析】（1）过点作，垂足为．
平面平面，两平面交线为， 平面，
平面，
由以及可得．
；
（2）①在平面上存在经过点的直线，使得．
证明：过点作，垂足为．
平面，平面，
，
又，平面，
平面，
平面，故可得，
即存在；
②在平面上不存在经过点的直线，使得，
证明：假设存在，
不在平面内，在平面内，则平面，
与平面矛盾．
不存在．
8．（2024·上海奉贤·一模）如图为正四棱锥为底面的中心．
(1)求证：平面，平面平面；
(2)设为上的一点，．
在下面两问中选一个，
①若，求直线与平面所成角的大小．
②已知平面与平面所成锐二面角的大小为，若，求的长．
【答案】(1)证明见解析
(2)选①，直线与平面所成角为；选②，
【分析】（1）利用线面平行的判定定理可得平面；线面垂直的判定定理可得平面；
（2）选①，以点为原点，所在的直线分别为轴的正方向建立空间直角坐标系，根据求出点坐标，再求出、平面的一个法向量，根据线面角的向量求法可得答案；选②，设，根据求出点坐标，求出平面、平面的一个法向量，由二面角的向量求法可得答案.
【解析】（1）因为底面是正方形，所以，
平面，平面，
所以平面；
，由四棱锥是正四棱锥，
可得平面，平面，所以，
由，平面，
所以平面，
又因为平面，所以平面平面；
（2）选①，如图，以点为原点，所在的直线分别为轴的
正方向建立空间直角坐标系，由，得
，
，，
由得，
所以，
因为平面，即平面，
所以是平面的一个法向量，
设直线与平面所成角为，
，
由，得，
所以直线与平面所成角为；
选②，同①以点为原点，所在的直线分别为轴的
正方向建立空间直角坐标系，设，得
，
，
由得，
所以，，
设为平面的一个法向量，
则得，令得，
所以，因为平面，
所以是平面的一个法向量，
设平面与平面所成锐二面角的大小为，得，
由，
解得，即.
1、求空间几何体的体积的常用方法
公式法
规则几何体的体积，直接利用公式
割补法
把不规则的几何体分割成规则的几何体，或者把不规则的几何体补成规则的几何体
等体积法
通过选择合适的底面来求几何体体积的一种方法，特别是三棱锥的体积
求空间几何体的表面积方法归纳：
(1)多面体的表面积是各个面的面积之和．
(2)旋转体的表面积是将其展开后，展开图的面积与底面面积之和．
(3)组合体的表面积求解时注意对衔接部分的处理．
3、证明平行关系的常用方法
熟练掌握线线、线面、面面平行关系间的相互转化是解决线线、线面、面面平行的综合问题的关键．面面平行判定定理的推论也是证明面面平行的一种常用方法．
4、(1)三种垂直的综合问题，一般通过作辅助线进行线线、线面、面面垂直间的转化．
(2)对于线面关系中的存在性问题，首先假设存在，然后在该假设条件下，利用线面关系的相关定理、性质进行推理论证．
5、(1)利用向量法证明平行、垂直关系，关键是建立恰当的坐标系(尽可能利用垂直条件，准确写出相关点的坐标，进而用向量表示涉及到直线、平面的要素)．
(2)向量证明的核心是利用向量的数量积或数乘向量，但向量证明仍然离不开立体几何的有关定理．
圆形截面
正方形截面
矩形截面
条件
r为圆半径
a为正方形边长
h为矩形的长，b为矩形的宽，
抗弯截面系数




极大值