初中数学沪科版（2024）七年级下册（2024）7.2 一元一次不等式课文内容ppt课件

这是一份初中数学沪科版（2024）七年级下册（2024）7.2 一元一次不等式课文内容ppt课件，共20页。PPT课件主要包含了观察下列不等式，它们有什么共同点，还能找出很多个，x＞25等内容，欢迎下载使用。
问题 某公司的统计资料表明，科研经费每增加 1 万元，年利润就增加 1.8 万元.如果该公司原来的年利润为 200 万元，要使年利润超过 245 万元，那么增加的科研经费应高于多少万元？
设该公司增加科研经费 x 万元，那么年利润就增加 1.8x 万元. 因为年利润要超过 245 万元，所以
200 + 1.8x > 245.
（1）x – 7 ≥ 2
（2）3x ＜ x+1
（4）– 4x ＞ 8
像这种含有一个未知数，未知数的次数是 1、且不等号两边都是整式的不等式叫做一元一次不等式.
对于不等式 200 + 1.8x > 245:
当 x 取 26 时，代入原不等式左边，得 200 + 1.8×26 = 246.8 ＞ 245. 当 x 取 25 时，代入原不等式左边，得 200 + 1.8×25 = 245 .当 x 取 24 时，代入原不等式左边，得 200 + 1.8×24 = 243. 2 ＜ 245.
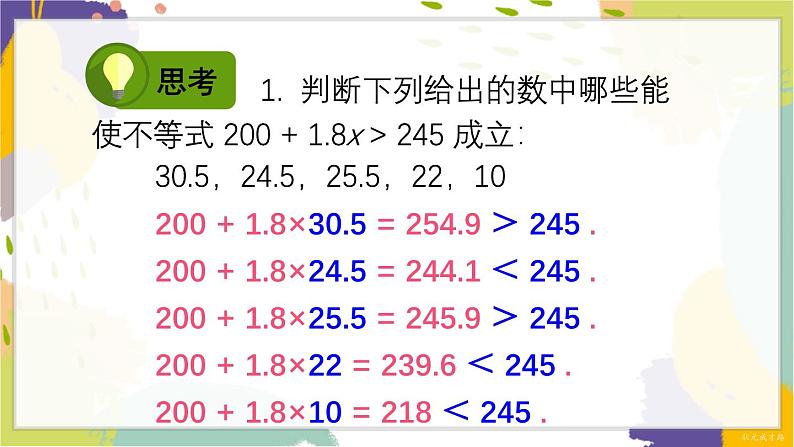
1. 判断下列给出的数中哪些能使不等式 200 + 1.8x > 245 成立：
200 + 1.8×30.5 = 254.9 ＞ 245 .
200 + 1.8×24.5 = 244.1 ＜ 245 .
200 + 1.8×25.5 = 245.9 ＞ 245 .
200 + 1.8×22 = 239.6 ＜ 245 .
200 + 1.8×10 = 218 ＜ 245 .
30.5，24.5，25.5，22，10
2. 你还能找出使上述不等式成立的其他数吗？能找多少个？
一般地，能够使不等式成立的未知数的值，叫做这个不等式的解，所有这些解的全体称为这个不等式的解集.
由上可知，不等式 200 + 1.8x > 245的解集是
求不等式解集的过程叫做解不等式.
例 1 解不等式：2x + 5 ≤ 7（2 – x）
解 去括号，得 2x + 5 ≤ 14 – 7x.
移项，得 2x + 7x ≤ 14 – 5.
合并同类项，得 9x ≤ 9.
x 系数化成1，得 x ≤ 1.
如 x ≤ 1，可用数轴上表示 1 的点以及左边所有点来表示.
不等式的解集可以在数轴上直观地表示出来.
（1）5x + 15 ≥ 4x – 1；
解 移项，得 5x – 4x ≥ – 1 – 15.
合并同类项，得 x ≥ – 16.
解下列不等式，并把它们的解集在数轴上表示出来：
（2）2（x + 5）≤ 3（x – 5）；
解：去括号得：2x + 10 ≤ 3x – 15；
移项得：2x – 3x ≤ – 15 – 10；
合并同类项得： – x ≤ – 25；
系数化为 1 得：x ≥ 25 .
将解集用数轴表示，则如右图：
1. 解下列不等式，并把它们的解集在数轴上表示出来： （1）3x + 2 ≤ 2x – 5；
解：移项得：3x – 2x ≤ – 5 – 2， 合并同类项得：x ≤ – 7.
（2）3（y + 2）– 1 ≥ 8 – 2（y – 1）.
解：去括号得：3y + 6 – 1 ≥ 8 – 2y + 2， 移项得：3y + 2y ≥ 8 + 2 + 1 – 6， 合并同类项得：5y ≥ 5， 系数化为 1 得：y ≥ 1，
2. 若关于 x 的不等式（m + 1）x ＜ 1 + m 的解集是 x ＜ 1，则满足的条件是什么？
解：（m + 1 ）x ＜ 1 + m， 因为 x ＜ 1， 所以 m+ 1 ＞ 0， 所以 m ＞ – 1.
3. 已知方程 ax + 12 = 0 的解是 x = 3，求不等式（a + 2）x＜ – 6 的解集.
解：由 ax + 12 = 0 的解是 x = 3， 得 a = – 4. 将 a = – 4 代入不等式（a + 2）x ＜ – 6 ， 得（ – 4 + 2）x ＜ – 6， 所以 x ＞ 3.
4. 已知 3x + 4 ≤ 6 + 2（x – 2），则 |x + 1| 的最小值是多少？
解：3x + 4 ≤ 6 + 2x – 4， 3x – 2x ≤ 6 – 4 – 4， 解得 x ≤ – 2.所以当 x = – 2 时，|x + 1| 的最小值为1.