冀教版（2024）30.1 二次函数课文课件ppt

这是一份冀教版（2024）30.1 二次函数课文课件ppt，共18页。PPT课件主要包含了学习目标，旧知回顾，一条直线，双曲线，情境引入，x＋80，一次函数，函数解析式是整式，二次项系数不为0，新知探究等内容，欢迎下载使用。
1.理解二次函数的定义2.掌握二次函数的一般形式及函数值3.运用二次函数的表达式表示实际问题
我们已经学习了哪些函数？它们的解析式是什么？
一次函数y＝kx＋b(k≠0)正比例函数y＝kx (k≠0)反比例函数
1.如图所示，用规格相同的正方形瓷砖铺成矩形地面，其中，横向瓷砖比纵向瓷砖每排多5块，矩形地面最外面一圈为灰色瓷砖，其余部分全为白色瓷砖.设纵向每排有n块瓷砖.
(1)设灰色瓷砖的总数为y块.用含n的代数式表示y，则y=_________.②y与n具有怎样的函数关系？设白色瓷砖的总数为z块.①用含n的代数式表z，则z=__________.②z是n的函数吗？说说理由.
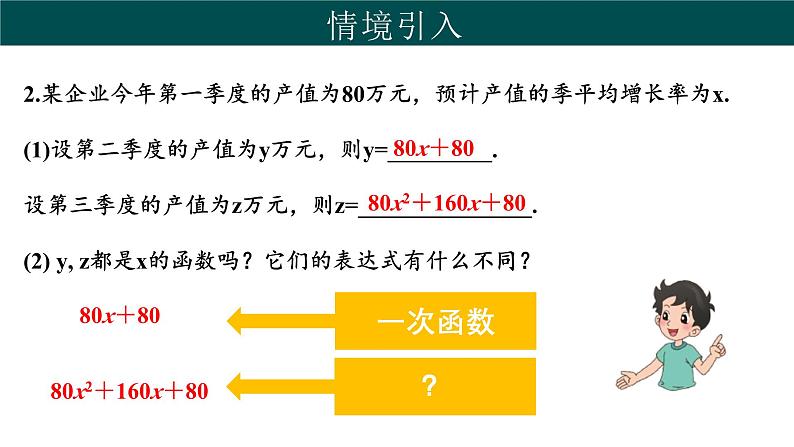
2.某企业今年第一季度的产值为80万元，预计产值的季平均增长率为x.(1)设第二季度的产值为y万元，则y=_________.设第三季度的产值为z万元，则z=_______________.(2) y, z都是x的函数吗？它们的表达式有什么不同？
80x2＋160x＋80
思考：函数z=n2＋n－6，z＝80x2＋160x＋80有什么共同点？
化简后自变量的最高次数是2；
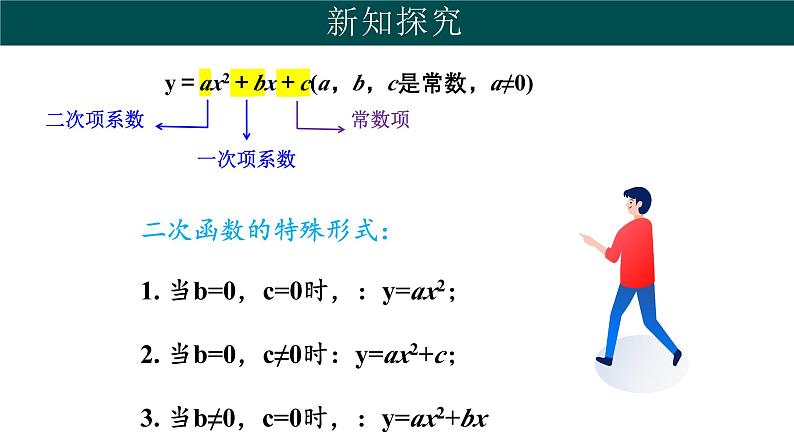
一般地，形如y＝ax2＋bx＋c(a，b，c是常数，a≠0)的函数，叫做二次函数．其中，x是自变量，a，b，c分别是函数解析式的二次项系数、一次项系数和常数项．
二次函数的特殊形式：1. 当b=0，c=0时，：y=ax2；2. 当b=0，c≠0时：y=ax2+c；3. 当b≠0，c=0时，：y=ax2+bx
y＝ax2＋bx＋c(a，b，c是常数，a≠0)
例1、下列函数中，哪些是二次函数？若是,分别指出二次项系数,一次项系数,常数项.
(6) y=x²+x³+25
(8)y=mx²+nx+p (m,n,p为常数）
(5)y=x-2+x
(9) y＝3(x－2)(x－5)
(10)y=(x+3)²－x²
(1)y＝7x－1；　 (2)y＝－5x2；　　　　　(3)y＝3a3＋2a2； (4)y＝x－2＋x；
二次项系数为－5，一次项系数为0，常数项为0.
(5)y＝3(x－2)(x－5)
整理得到y＝3x2－21x＋30，
二次项系数为3，一次项系数为－21，常数项为30.
把函数 化成一般形式，写出各项系数。
y=(5x+7)(x-3)+2x-5 =5x2-8x-21+2x-5 =5x2-6x-26它是二次函数,二次项系数及常数项分别是5,-6,-26
y=(5x+7)(x-3)+2x-5
函数值：确定一个x的值，代入二次函数表达式中所得的y值为函数值.
当已知函数y＝x2－2x+1(1)当x＝－1时，函数值为多少？(2)当x为多少时，函数值为0.
(1)当x＝－1时，y＝(-1)2－3×(-1)+1＝-1(2)当y＝0时，x2－2x+1＝0，解得x1＝x2＝1
求函数值及自变量的值，只要把对应的自变量x的值及函数值y代入函数表达式即可．
当已知函数y＝x2－2x-3(1)当x＝1时，函数值为多少？(2)当x为多少时，函数值为-3.
(1)当x＝1时，y＝12－2×1-3＝-4(2)当y＝-3时，x2－2x＝0，解得x1＝2，x2＝0
根据实际问题列二次函数的解析式，一般要经历以下几个步骤： 1）先找出题目中有关两个变量之间的等量关系； 2）然后用题设的变量或数值表示这个等量关系； 3）列出相应二次函数的关系式。
n个学生加聚会，每两个人之间握一次手.握手次数m与人数n有什么关系？
一块长方形草地，它的长比宽多2m. 设它的长为xm，面积为ym2，请写出用x表示y的函数表达式. y是x的二次函数吗？若是，请指出相应的a，b，c的值.
y＝x·(x－2)＝x2－2x.y是x的二次函数．a＝1，b＝－2，c＝0.
1.若 是二次函数．(1)求k的值．(2)当x=1时，求y的值．
2.某果园有100棵橙子树，每一棵树平均结600个橙子。现准备多种一些橙子树以提高产量，但是如果多种树，那么树之间的距离和每一棵树所接受的阳光就会减少．根据经验估计，每多种一棵树，平均每棵树就会少结5个橙子。假设果园增种x棵橙子树,果园橙子的总产量为y个,请你写出y与x之间的关系式．
y= (100+x) (600-5x)
=-5x2+100x+60000
1.定义：一般地,形如y=ax²+bx+c(a,b,c是常数,a≠0)的函数叫做x的二次函数.其中,是x自变量,a,b,c分别是函数表达式的二次项系数、一次项系数和常数项. y=ax²+bx+c(a,b,c是常数,a≠0)的几种不同表示形式: (1)y=ax²(a≠0,b=0,c=0,). (2)y=ax²+c(a≠0,b=0,c≠0). (3)y=ax²+bx(a≠0,b≠0,c=0). 2.定义的实质是：ax²+bx+c是整式,自变量x的最高次数是二次,自变量x的取值范围是全体实数.