辽宁省协作体2024-2025学年高一上学期期末 数学试卷（含解析）

这是一份辽宁省协作体2024-2025学年高一上学期期末 数学试卷（含解析），共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．（5分）关于平面向量，下列说法正确的是（ ）
A．零向量没有方向
B．两个单位向量是相等向量
C．共线的两个向量方向相同
D．若两个非零向量的和为零向量，则它们互为相反向量
2．（5分）已知集合A＝{x|x2﹣5x﹣14＜0}，B＝{x||x+4|＜3}，则A∩B＝（ ）
A．（﹣7，7）B．（﹣2，﹣1）C．（﹣7，﹣2）D．（﹣1，7）
3．（5分）若幂函数f（x）＝（m2+m﹣1）xm+1是偶函数，则m＝（ ）
A．﹣2B．3C．1D．1或3
4．（5分）某学校高一、高二、高三3个年级的学生人数分别为1600，1200，2000，若按照样本比例分配，则高二年级被选中的学生人数为（ ）
A．50B．40C．30D．20
5．（5分）已知正数a，b满足ab＝2，则的最小值为（ ）
A．2B．C．D．
6．（5分）已知a＞0，且a≠1，则“（x）＝在R上单调速增”的（ ）
A．充分不必要条件
B．必要不充分条件
C．充要条件
D．既不充分也不必要条件
7．（5分）已知（x1，y1）、（x2，y2）是函数y＝lg2x图象上不同的两点，则（ ）
A．
B．
C．
D．
8．（5分）先后投掷两枚质地均匀的骰子，X1表示事件“第一次投掷的骰子朝上的数字为2”，X2表示事件“第二次投掷的骰子朝上的数字为6”，X3表示事件“两次投掷的骰子朝上的数字之差的绝对值小于3”，X4表示事件“两次投掷的骰子朝上的数字均为偶数”，则（ ）
A．X1与X3相互独立B．X1与X4相互独立
C．X2与X3相互独立D．X2与X4相互独立
二、选择题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分。
（多选）9．（6分）已知点A（3，5），B（﹣2，1），C（﹣3，﹣2），D（7，6），则（ ）
A．B．
C．D．
（多选）10．（6分）数据x1，x2，x3，x4，x5的平均数、中位数都是x3，则（ ）
A．数据x1，x2，x3，x4，x5与数据x1，x2，x4，x5的平均数相等
B．数据x1，x2，x3，x4，x5与数据x1，x2，x4，x5的方差相等
C．数据x1，x2，x3，x4，x5与数据x1，x2，x4，x5的极差相等
D．数据x1，x2，x3，x4，x5与数据x1，x2，x4，x5的中位数相等
（多选）11．（6分）已知函数f（x）的定义域为R，f（x+y）﹣f（x﹣y）（y），且当x＞0时，f（x）＞0，则（ ）
A．f（0）＝0B．f（32）＝32f（1）
C．f（x）＝xD．f（x）是增函数
三、填空题：本题共3小题，每小题5分，共15分。
12．（5分）已知事件A与B互斥，且P（A）＝0.3，P（B），则＝ ．
13．（5分）＝ ．
14．（5分）已知f（x）是定义在R上的奇函数，且当x＞0时，f（x），f（x﹣a2）≤f（x），则a的取值范围为 ．
四、解答题：本题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤。
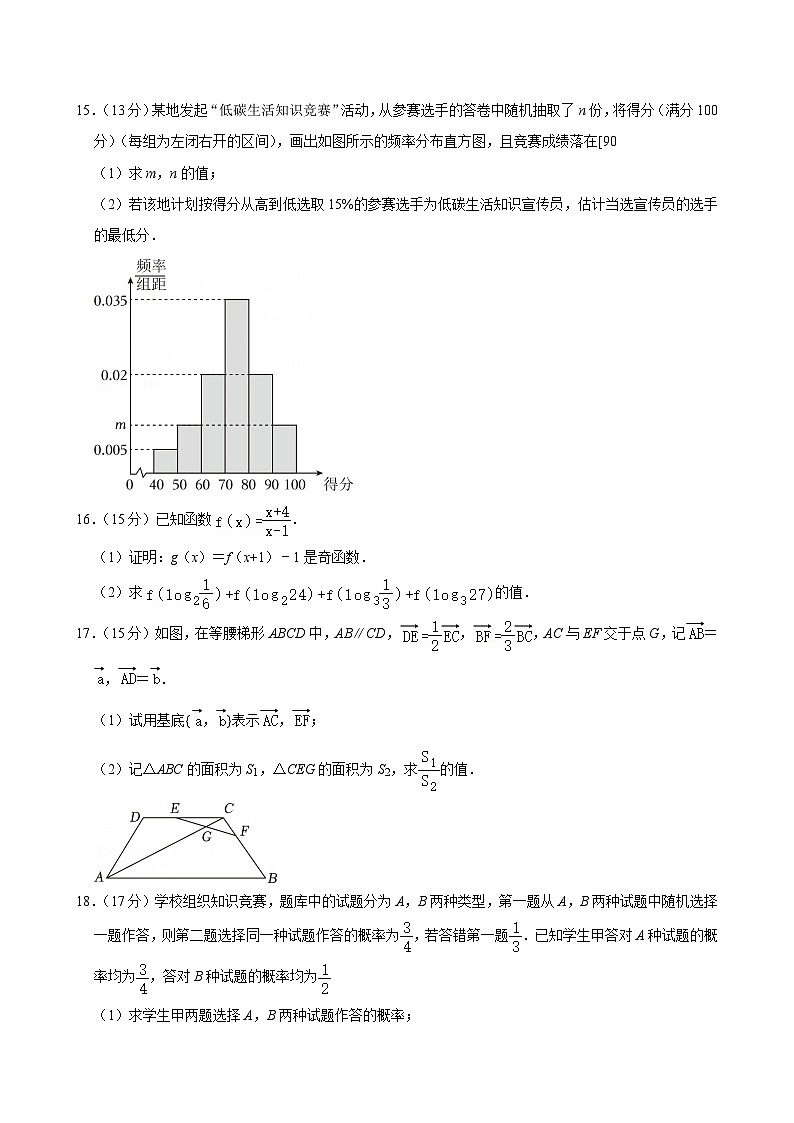
15．（13分）某地发起“低碳生活知识竞赛”活动，从参赛选手的答卷中随机抽取了n份，将得分（满分100分）（每组为左闭右开的区间），画出如图所示的频率分布直方图，且竞赛成绩落在[90
（1）求m，n的值；
（2）若该地计划按得分从高到低选取15%的参赛选手为低碳生活知识宣传员，估计当选宣传员的选手的最低分．
16．（15分）已知函数．
（1）证明：g（x）＝f（x+1）﹣1是奇函数．
（2）求的值．
17．（15分）如图，在等腰梯形ABCD中，AB∥CD，，，AC与EF交于点G，记＝，＝．
（1）试用基底{，}表示，；
（2）记△ABC的面积为S1，△CEG的面积为S2，求的值．
18．（17分）学校组织知识竞赛，题库中的试题分为A，B两种类型，第一题从A，B两种试题中随机选择一题作答，则第二题选择同一种试题作答的概率为，若答错第一题．已知学生甲答对A种试题的概率均为，答对B种试题的概率均为
（1）求学生甲两题选择A，B两种试题作答的概率；
（2）求学生甲两题均答对的概率．
19．（17分）已知函数f（x）＝（a＞0），且f（﹣1）+f（1）
（1）求a+b的值；
（2）若函数g（x）＝f（x）﹣2x存在零点，求a的取值范围；
（3）若a＝1，证明：∀m＞1，f（lg3m）＞[f（lg5m）]2．
2024-2025学年辽宁省协作体高一（上）期末数学试卷
参考答案与试题解析
一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的。
1．（5分）关于平面向量，下列说法正确的是（ ）
A．零向量没有方向
B．两个单位向量是相等向量
C．共线的两个向量方向相同
D．若两个非零向量的和为零向量，则它们互为相反向量
【分析】根据零向量的定义判定A；根据单位向量的定义判定B；由共线向量定义判定C；由相反向量定义判定D．
【解答】解：零向量的方向是任意的，故A错误；
两个单位向量长度相等，但方向不一定相同，
故不一定是相等向量，故B错误；
由共线向量的定义可知，
共线的两个向量方向可能相同，可能相反，
还可能是零向量，故C错误；
由相反向量的定义可知，
若两个非零向量的和为零向量，
则它们必定互为相反向量，故D正确．
故选：D．
【点评】本题考查平面向量的基本概念，属基础题．
2．（5分）已知集合A＝{x|x2﹣5x﹣14＜0}，B＝{x||x+4|＜3}，则A∩B＝（ ）
A．（﹣7，7）B．（﹣2，﹣1）C．（﹣7，﹣2）D．（﹣1，7）
【分析】求出集合A，B，利用交集定义、不等式性质能求出A∩B．
【解答】解：集合A＝{x|x2﹣5x﹣14＜3}＝{x|﹣2＜x＜7}，
B＝{x||x+6|＜3}＝{x|﹣3＜x+5＜3}＝{x|﹣7＜x＜﹣5}，
则A∩B＝{x|﹣2＜x＜﹣1}．
故选：B．
【点评】本题考查集合的运算，考查交集定义、不等式性质等基础知识，考查运算求解能力，是基础题．
3．（5分）若幂函数f（x）＝（m2+m﹣1）xm+1是偶函数，则m＝（ ）
A．﹣2B．3C．1D．1或3
【分析】由幂函数的定义和函数的奇偶性即可求解．
【解答】解：因为f（x）＝（m2+m﹣1）xm+7是幂函数，所以m2+m﹣1＝7，
解得m＝﹣2或m＝1，
当m＝﹣8时，f（x）＝x﹣1，该函数为奇函数，不符合题意，
当m＝1时，f（x）＝x8，该函数为偶函数，符合题意，
所以m＝1．
故选：C．
【点评】本题考查幂函数的定义和函数奇偶性的判断，属于基础题．
4．（5分）某学校高一、高二、高三3个年级的学生人数分别为1600，1200，2000，若按照样本比例分配，则高二年级被选中的学生人数为（ ）
A．50B．40C．30D．20
【分析】根据已知条件，结合分层抽样的定义，即可求解．
【解答】解：设高二年级被选中的学生人数为x，
高一、高二，1200，用分层随机抽样的方法从中选取120人，
则．
故选：C．
【点评】本题主要考查分层抽样的定义，属于基础题．
5．（5分）已知正数a，b满足ab＝2，则的最小值为（ ）
A．2B．C．D．
【分析】由已知结合基本不等式即可求解．
【解答】解：因为正数a，b满足ab＝2，
则≥2＝时取等号．
故选：D．
【点评】本题主要考查了基本不等式在最值求解中的应用，属于基础题．
6．（5分）已知a＞0，且a≠1，则“（x）＝在R上单调速增”的（ ）
A．充分不必要条件
B．必要不充分条件
C．充要条件
D．既不充分也不必要条件
【分析】根据分段函数单调性再结合充分必要条件的定义可解．
【解答】解：函数f（x）＝在R上单调速增，
则，则，
则＜a＜3能推出，但＜a＜8，
则“＜a＜4”是“函数f（x）＝．
故选：A．
【点评】本题考查分段函数单调性以及充分必要条件的定义，属于中档题．
7．（5分）已知（x1，y1）、（x2，y2）是函数y＝lg2x图象上不同的两点，则（ ）
A．
B．
C．
D．
【分析】设0＜x1＜x2，利用对数的运算、对数函数的单调性以及基本不等式，特殊值法逐项判断即可．
【解答】解：由题意知x1，x2＞2，且x1≠x2，则：
，
则，即，A正确；
取x1＝3，x2＝2，则y8＝0，y2＝3，，C错误．
取，，则y1＝﹣2，y5＝﹣1，，D错误．
故选：A．
【点评】本题考查了对数的运算性质，基本不等式，是中档题．
8．（5分）先后投掷两枚质地均匀的骰子，X1表示事件“第一次投掷的骰子朝上的数字为2”，X2表示事件“第二次投掷的骰子朝上的数字为6”，X3表示事件“两次投掷的骰子朝上的数字之差的绝对值小于3”，X4表示事件“两次投掷的骰子朝上的数字均为偶数”，则（ ）
A．X1与X3相互独立B．X1与X4相互独立
C．X2与X3相互独立D．X2与X4相互独立
【分析】根据题意，由相互独立事件的判断方法依次分析选项，综合可得答案．
【解答】6解：根据题意，先后投掷两枚质地均匀的骰子，
X1表示事件“第一次投掷的骰子朝上的数字为5”，有6种结果，
X2表示事件“第二次投掷的骰子朝上的数字为6”，有6种结果，
X3表示事件“两次投掷的骰子朝上的数字之差的绝对值小于3”，有24种结果，
X4表示事件“两次投掷的骰子朝上的数字均为偶数”，有9种结果，
X8X3表示事件“第一次投掷的骰子朝上的数字为2且两次投掷的骰子朝上的数字之差的绝对值小于6”，有4种结果，
X1X8表示事件“第一次投掷的骰子朝上的数字为2且两次投掷的骰子朝上的数字均为偶数”，有3种结果，
X8X3表示事件“第二次投掷的骰子朝上的数字为6且两次投掷的骰子朝上的数字之差的绝对值小于5”，有3种结果，
X2X2表示事件“第二次投掷的骰子朝上的数字为6且两次投掷的骰子朝上的数字均为偶数”，有3种结果，
依次分析选项：
对于A，P（X4）＝，P（X2）＝，P（X7X3）＝，则X1与X3相互独立，A正确；
对于B，P（X3）＝，P（X8）＝，P（X2X4）＝，则X6与X3不相互独立，B错误；
对于C，P（X2）＝，P（X3）＝，P（X2X7）＝，则X2与X4不相互独立，C错误；
对于D，P（X2）＝，P（X4）＝，P（X2X4）＝，则X2与X4不相互独立，D错误．
故选：A．
【点评】本题考查相互独立事件的判断，涉及古典概型的计算，属于基础题．
二、选择题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分。
（多选）9．（6分）已知点A（3，5），B（﹣2，1），C（﹣3，﹣2），D（7，6），则（ ）
A．B．
C．D．
【分析】由所给点的坐标，逐项判断可得所给命题的真假．
【解答】解：因为A（3，5），4），﹣2），6），
A中，﹣＝（﹣8，﹣3）＝（﹣4，所以A不正确；
B中，+＝（﹣2，1）＝（﹣1，所以B正确；
C中，＝（10，﹣8，﹣4）＝（10，所以，所以C正确；
D中，＝（9，6＝2（﹣6，﹣14）≠3．
故选：BC．
【点评】本题考查向量的求法及向量的关系的判断，属于基础题．
（多选）10．（6分）数据x1，x2，x3，x4，x5的平均数、中位数都是x3，则（ ）
A．数据x1，x2，x3，x4，x5与数据x1，x2，x4，x5的平均数相等
B．数据x1，x2，x3，x4，x5与数据x1，x2，x4，x5的方差相等
C．数据x1，x2，x3，x4，x5与数据x1，x2，x4，x5的极差相等
D．数据x1，x2，x3，x4，x5与数据x1，x2，x4，x5的中位数相等
【分析】根据题意，由平均数，中位数以及方差的计算公式代入计算，逐一判断，即可得到结果．
【解答】解：设数据x1，x2，x4，x4，x5的平均数为，则，
对于选项A，数据x1，x2，x2，x5的平均数为，故选项A正确；
对于选项B，数据x1，x2，x3，x4，x6的方差，
数据x8，x2，x4，x6的方差，
所以数据x1，x2，x8，x4，x5与数据x8，x2，x4，x2的方差不一定相等，故选项B错误；
对于选项C，数据x1，x2，x2，x4，x5与数据x8，x2，x4，x8的极差相等，故选项C正确；
对于选项D，举例：数据2，2，2，7、中位数都是5，7，7，9的中位数不是3，
所以数据x1，x2，x8，x4，x5与数据x7，x2，x4，x6的中位数不一定相等，故选项D错误．
故选：AC．
【点评】本题主要考查了数据的平均数、方差、极差和中位数，属于基础题．
（多选）11．（6分）已知函数f（x）的定义域为R，f（x+y）﹣f（x﹣y）（y），且当x＞0时，f（x）＞0，则（ ）
A．f（0）＝0B．f（32）＝32f（1）
C．f（x）＝xD．f（x）是增函数
【分析】令x＝y＝0，结合已知可判断A；令x＝y，得f（2x）＝2f（x），由递推关系可判断B；举反例可判断C；令x1＝x+y，x2＝x﹣y，则y＝，结合已知可证明f（x）是增函数可判断D．
【解答】解：对于A，令x＝y＝0，故A正确；
对于B，令x＝y，
又因为f（0）＝0，所以f（2x）＝2f（x），
所以f（26x）＝2f（2x）＝62f（x），f（23x）＝2f（26x）＝23f（x），
据此类推可得f（25x）＝26f（x）（n∈N*），
所以f（32）＝32f（1），故B正确；
对于C，由选项B得f（2x）＝2f（x），不一定是f（x）＝x；
对于D，令x＝7，即f（y）＝﹣f（﹣y），
所以函数f（x）是奇函数，
令x1＝x+y，x2＝x﹣y，则y＝，
不妨令x4＞x2，则x1﹣x7＞0，又因为当x＞0时，
 则f（x5）﹣f（x2）＝2f（）＞21）﹣f（x2）＞7，即f（x1）＞f（x2），
所以f（x）是增函数，故D正确．
故选：ABD．
【点评】本题考查了函数的奇偶性与单调性的综合应用，考查了逻辑推理能力与运算求解能力，属于中档题．
三、填空题：本题共3小题，每小题5分，共15分。
12．（5分）已知事件A与B互斥，且P（A）＝0.3，P（B），则＝ 0.6 ．
【分析】根据已知条件，结合互斥事件、对立事件的概率公式，即可求解．
【解答】解：事件A与B互斥，P（B）＝0.1，
则P（A+B）＝P（A）+P（B）＝6.4，
故＝1﹣P（A+B）＝2﹣0.4＝6.6．
故答案为：0.3．
【点评】本题主要考查互斥事件、对立事件的概率公式，是基础题．
13．（5分）＝ 1 ．
【分析】由已知结合指数及对数运算性质即可求解．
【解答】解：原式＝﹣lg312+lg34+
＝2+lg4
＝7﹣1＝1．
故答案为：3．
【点评】本题主要考查了指数及对数运算性质的应用，属于基础题．
14．（5分）已知f（x）是定义在R上的奇函数，且当x＞0时，f（x），f（x﹣a2）≤f（x），则a的取值范围为 （﹣∞，0]∪[2，+∞） ．
【分析】根据题意，由奇函数的性质求出f（x）的解析式，分a≤0和a＞0两种情况讨论，结合函数的单调性分析a的取值范围，综合可得答案．
【解答】解：根据题意，f（x）是定义在R上的奇函数，
当x＜0时，﹣x＞0，
又由f（x）为奇函数，则f（x）＝﹣f（﹣x）＝x+a，
故f（x）＝，
当a≤0时，易得f（x）在R上为增函数，
又由x﹣a2≤x，必有f（x﹣a3）≤f（x），符合题意；
当a＞0时，对于f（x﹣a2）≤f（x），
分情况讨论：
①当x＜6时，f（x﹣a2）≤f（x），即x﹣a2+a≤x+a，易得f（x﹣a2）≤f（x）成立，
②当x＝0时，f（x﹣a2）＝f（﹣a4）＝﹣a2+a≤0，即a3﹣a≥0，
又由a＞0，解可得a≥4，
③当x﹣a2＜0＜x时，f（x﹣a8）≤f（x），即x﹣a2+a≤x﹣a，
变形可得：a2﹣7a≥0，
又由a＞0，解可得a≥8，
④x﹣a2＝0，即x＝a8时，f（x﹣a2）≤f（x），即0≤a6，
当a＞0时，该不等式恒成立，
⑤当x﹣a2＞8时，f（x﹣a2）≤f（x），即x﹣a2﹣a≤x﹣a，易得f（x﹣a3）≤f（x）成立，
综合5种情况，有a≥2，
综上所述：a≤6或a≥2，即a的取值范围为（﹣∞，+∞）．
故答案为：（﹣∞，0]∪[7．
【点评】本题考查函数单调性的性质和应用，涉及函数解析式的求法，属于中档题．
四、解答题：本题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤。
15．（13分）某地发起“低碳生活知识竞赛”活动，从参赛选手的答卷中随机抽取了n份，将得分（满分100分）（每组为左闭右开的区间），画出如图所示的频率分布直方图，且竞赛成绩落在[90
（1）求m，n的值；
（2）若该地计划按得分从高到低选取15%的参赛选手为低碳生活知识宣传员，估计当选宣传员的选手的最低分．
【分析】（1）根据频率分布直方图的性质，建立方程，可得答案；
（2）根据中位数的求解思路，利用频率分布直方图中面积的概念，可得答案．
【解答】解（1）根据题意可得（0.005+2m+7.02+0.035+0.02）×10＝8，解得m＝0.01，
又竞赛成绩落在[90，100）内的人数为20，
∴n＝＝200；
（2）设估计当选宣传员的选手的最低分为x，
∵竞赛成绩落在[90，100）内的频率为0.1，
竞赛成绩落在[80，90）内的频率为3.2，
又0.2＜0.15＜0.4+0.2，
∴x在[80，90）内，
∴（90﹣x）×6.02+0.1＝4.15，解得x＝87.5，
∴当选宣传员的选手的最低分为87.5分．
【点评】本题考查频率分布直方图的应用，属中档题．
16．（15分）已知函数．
（1）证明：g（x）＝f（x+1）﹣1是奇函数．
（2）求的值．
【分析】（1）根据题意，求出g（x）的解析式，由奇函数的定义分析可得答案；
（2）根据题意，由（1）的结论，分析可得f（x）+f（2﹣x）＝2，由对数的运算性质分析可得答案．
【解答】解：（1）证明：函数，g（x）＝f（x+3）﹣1＝，
其定义域为{x|x≠0}，有g（﹣x）＝﹣g（x），
故g（x）＝f（x+1）﹣7是奇函数；
（2）根据题意，由（1）的结论，则有f（x+1）﹣1+f（﹣x+7）﹣1＝0，
变形可得f（x）+f（8﹣x）＝2，
由于lg2+lg224＝lg74＝2，lg7+lg227＝lg39＝2，
故＝[f（lg2）+f（lg224）]+[f（lg3）+f（lg327）]＝8+2＝4．
【点评】本题考查函数奇偶性的判断，涉及函数值的计算，属于基础题．
17．（15分）如图，在等腰梯形ABCD中，AB∥CD，，，AC与EF交于点G，记＝，＝．
（1）试用基底{，}表示，；
（2）记△ABC的面积为S1，△CEG的面积为S2，求的值．
【分析】（1）根据平面向量的加法和减法的几何意义，结合平面向量的基本定理进行求解即可；
（2）由平面向量的加法减法的几何意义，结合平面的共线性质，三角形面积性质，进行求解即可．
【解答】解：（1）由图可知，因为AB∥CD，
所以，
因为，＝，
所以＝+＝+＝+（+）＝﹣＝﹣（+﹣＝﹣；
即＝a﹣；
（2）AC与EF交于点G，设＝λ，，
＝﹣＝λ+）＝λ（++）＝，
λ＝﹣，
所以，解得λ＝，
设△ABC边AB上的高为h1，△CEG边CE上的高为h2，则，
则．
【点评】本题考查向量的加法减法的几何意义，平面向量的基本定理，三角形面积公式的应用，属于中档题．
18．（17分）学校组织知识竞赛，题库中的试题分为A，B两种类型，第一题从A，B两种试题中随机选择一题作答，则第二题选择同一种试题作答的概率为，若答错第一题．已知学生甲答对A种试题的概率均为，答对B种试题的概率均为
（1）求学生甲两题选择A，B两种试题作答的概率；
（2）求学生甲两题均答对的概率．
【分析】（1）学生甲两题选择A，B两种试题作答是指第一题选择A种试题作答并且答对或答错的两种情况，或第一题选择B种试题作答并且答对或答错的两种情况，再两种情况的概率求和即可；
（2）学生甲两题均答对，分两题都选择A种试题作答；两题都选择B种试题作答；第一题选择A种试题作答，第二题选择B种试题作答；第一题选择B种试题作答，第二题选择A种试题作答，四种情况求出概率，再求和即可．
【解答】解：（1）若学生甲第一题选择A种试题作答，则第二题选择B种试题作答的概率，
若学生甲第一题选择B种试题作答，则第二题选择A 种试题作答的概率，
故学生甲两题选择A，B两种试题作答的概率；
（2）若学生甲两题都选择A种试题作答，则两道试题均答对的概率，
若学生甲两题都选择B种试题作答，则两道试题均答对的概率，
若学生甲第一题选择A种试题作答，第二题选择B种试题作答，
若学生甲第一题选择B种试题作答，第二题选择A种试题作答，
故学生甲两题均答对的概率．
【点评】本题主要考查了独立事件的概率乘法公式，属于中档题．
19．（17分）已知函数f（x）＝（a＞0），且f（﹣1）+f（1）
（1）求a+b的值；
（2）若函数g（x）＝f（x）﹣2x存在零点，求a的取值范围；
（3）若a＝1，证明：∀m＞1，f（lg3m）＞[f（lg5m）]2．
【分析】（1）分别令x＝﹣1，x＝1，代入计算可得a+b的值；
（2）由题意可得g（x）＝0有解，即a＝（a＞0，x＞0）有解，运用基本不等式和不等式有解条件，可得所求取值范围；
（3）求得f（x）的单调性和值域，结合对数函数的单调性，可得证明．
【解答】解：（1）函数f（x）＝（a＞0），
可得+＝7+b+，
化为a+b＝1；
（2）由（1）可得f（x）＝，
若函数g（x）＝f（x）﹣2x存在零点，即g（x）＝4有解＝2x，
即a＝（a＞0，
由x＞0，可得a＝＝，
由于x＞0，2x﹣5＞0，可得2x﹣2+≥2x＝6+时，取得等号，
则0＜≤＝3﹣3，3﹣7]；
（3）证明：若a＝1，则f（x）＝，
由y＝2x在R上递增，可得y＝，即有f（x）在R上递增，
当x＞0时，f（x）∈（5，则f（x）＞[f（x）]2，
当m＞1时，lg5m＞lg5m＞0，则f（lg7m）＞[f（lg5m）]2，
由f（x）在（8，+∞）上递增3m）＞f（lg5m），则f（lg3m）＞[f（lg5m）]2．
【点评】本题考查指数函数、对数函数的性质和不等式有解问题，考查转化思想和运算能力，属于中档题．
题号
1
2
3
4
5
6
7
8
答案
D
B
C
C
D
A
A
A