


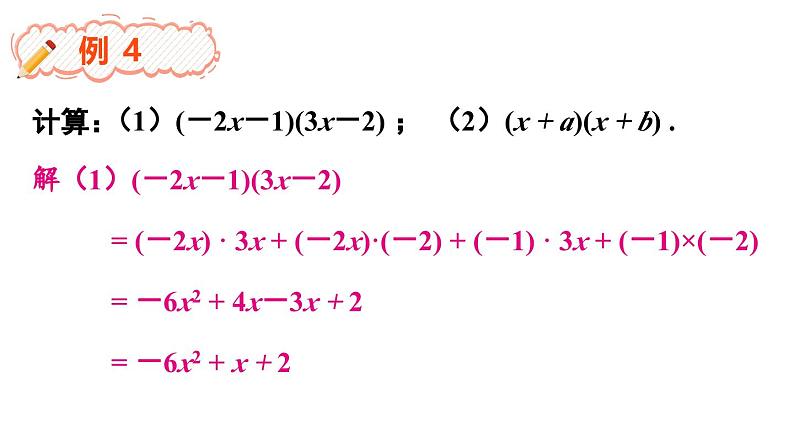

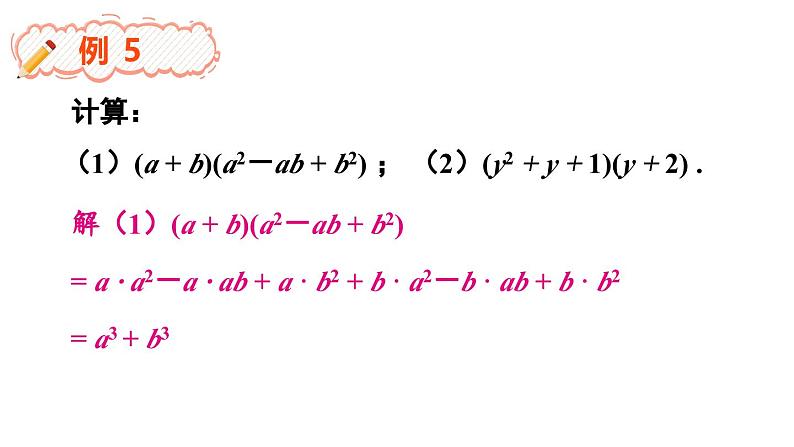
所属成套资源:沪科版(2024)七年级数学下册同步教学课件
初中数学8.2 整式乘法教学演示ppt课件
展开
这是一份初中数学8.2 整式乘法教学演示ppt课件,共17页。PPT课件主要包含了单项式与单项式相乘,-6a3b4c,单项式与多项式相乘,a+bm,+bm,+an,+bn,+a+bn,a3+b3,9x2-y2等内容,欢迎下载使用。
(2a2b3c)(-3ab)
x(x-1) + 2x(x + 1)-3x(2x-5)
= x2-x + 2x2 + 2x-6x2 +15x
= (x2 + 2x2-6x2) + (2x -x + 15x)
= -3x2 + 16x
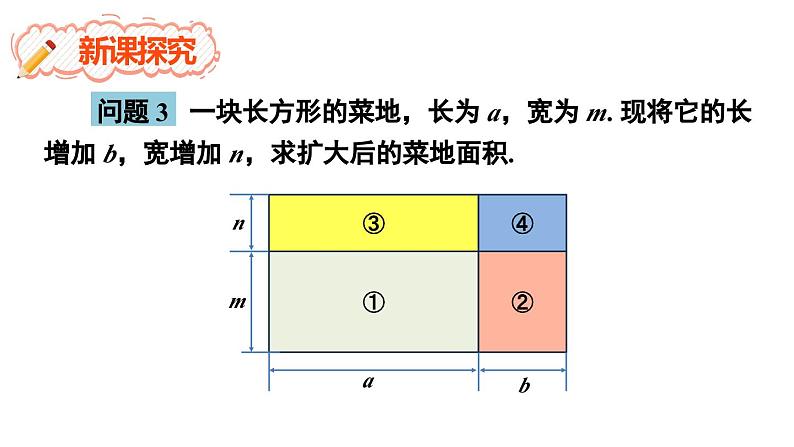
问题 3 一块长方形的菜地,长为 a,宽为 m. 现将它的长增加 b,宽增加 n,求扩大后的菜地面积.
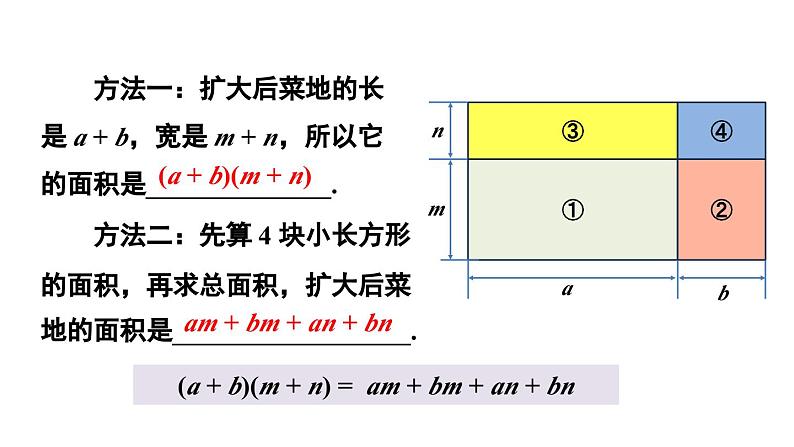
方法一:扩大后菜地的长是 a + b,宽是 m + n,所以它的面积是______________.
方法二:先算 4 块小长方形的面积,再求总面积,扩大后菜地的面积是__________________.
(a + b)(m + n)
am + bm + an + bn
(a + b)(m + n) = am + bm + an + bn
把 (a + b) 看成一个整体
= am + bm + an + bn
(a + b)(m + n) =
多项式与多项式的乘法法则:
多项式与多项式相乘,先用一个多项式的每一项与另一个多项式的每一项相乘,再把所得的积相加.
(1)(-2x-1)(3x-2) ;
(2)(x + a)(x + b) .
解(1)(-2x-1)(3x-2)
= (-2x) · 3x + (-2x)·(-2) + (-1) · 3x + (-1)×(-2)
= -6x2 + 4x-3x + 2
= -6x2 + x + 2
(1)(-2x-1)(3x-1) ;
(2)(x + a)(x + b)
= x2 + bx + ax + ab
= x2 + (a + b)x + ab
(1)(a + b)(a2-ab + b2) ;
(2)(y2 + y + 1)(y + 2) .
解(1)(a + b)(a2-ab + b2)
= a · a2-a · ab + a · b2 + b · a2-b · ab + b · b2
(2)(y2 + y + 1)(y + 2)
= y3 + 2y2 + y2 + 2y + y + 2
= y3 + 3y2 + 3y + 2
(1)(2n + 6)(n - 3) ; (2)(-3x-1)(-x2 + 1).
解 (1)(2n + 6)(n - 3)
= 2n· n + 2n · (-3) + 6n + 6×(-3)
= 2n2 - 18 .
(2)(-3x-1)(-x2 + 1)
= (-3x)·(-x2) + (-3x)·1 + (-1)·(-x2) + (-1)·1
= 3x3-3x + x2 -1
(1)(3x - y)(3x + y) ; (2)(3a + 2)(3a-2)-9a(a-1).
解(1)(3x - y)(3x + y)
= 3x · 3x + 3x · y + (-y)(3x) + (-y) · y
= 9x2 + 3xy -3xy-y2
(2)(3a + 2)(3a-2)-9a(a-1)
= 3a · 3a + 3a·(-2) + 6a + 2·(-2) +(-9a)a + (-9a)(-1)
= 9a2 -6a + 6a-4 -9a2 + 9a
(3)(x- y)(x2 + xy + y2) ; (4)(x + 1)(x2-2x + 3).
(3)(x- y)(x2 + xy + y2)
= x3 + x2y + xy2 +(-y)·x2 + (-y)·xy + (-y)·y2
= x3 + x2y + xy2 -x2y -xy2 -y3
(4)(x + 1)(x2-2x + 3)
= x3 -2x2 + 3x + x2 -2x + 3
= x3 -x2 + x + 3
3. 先化简,再求值:(x-4)(x-2)-(x-1)(x + 3),
解 (x-4)(x-2)-(x-1)(x + 3)
= x2-2x-4x + 8-(x2 + 3x -x-3)
= -8×(-2) + 11
相关课件
这是一份初中数学沪科版(2024)七年级下册(2024)第8章 整式乘法与因式分解8.2 整式乘法教学演示ppt课件,共15页。PPT课件主要包含了na+b+c,3a2等内容,欢迎下载使用。
这是一份初中沪科版(2024)8.2 整式乘法集体备课课件ppt,共18页。PPT课件主要包含了幂的运算性质,乘法交换律,乘法结合律,同底数幂的乘法,x3y3,-15a2b2c,C2πr,nCn·2πr等内容,欢迎下载使用。
这是一份沪科版七年级下册8.2 整式乘法教课课件ppt,共15页。PPT课件主要包含了答案呈现,x2+7x+12,x2-x-12,x2+x-12,x2-7x+12等内容,欢迎下载使用。










