人教A版（2019）高一数学必修第一册三角函数的图象与性质应用(2)-教学设计

这是一份人教A版（2019）高一数学必修第一册三角函数的图象与性质应用(2)-教学设计，共5页。
课例编号
2020QJ10SXRA054
学科
数学
年级
高一
学期
第一学期
课题
三角函数的图象与性质应用（2）
教科书
书名：高中数学必修一
出版社：人民教育出版社 出版日期：2019年6月
教学人员
姓名
单位
授课教师
田会永
北京汇文中学
指导教师
李颖
东城区教师研修中心
教学目标
教学目标：
１．进一步理解三角函数的图象与性质，会利用三角函数的图象和性质解决相关函数最大（小）值的问 题，以及利用图象和性质会解一些特殊的不等式；
２．在解决问题的过程中体会数形结合思想和转化与化归思想的应用，加深知识间的内在联系；
３．在知识的运用过程中发展数学运算和数学直观的素养.
教学重点：利用三角函数图象及性质解决相关函数的问题.
教学难点：问题解决过程中方法的选择及转化策略的使用.
教学过程
时间
教学环节
主要师生活动
复习
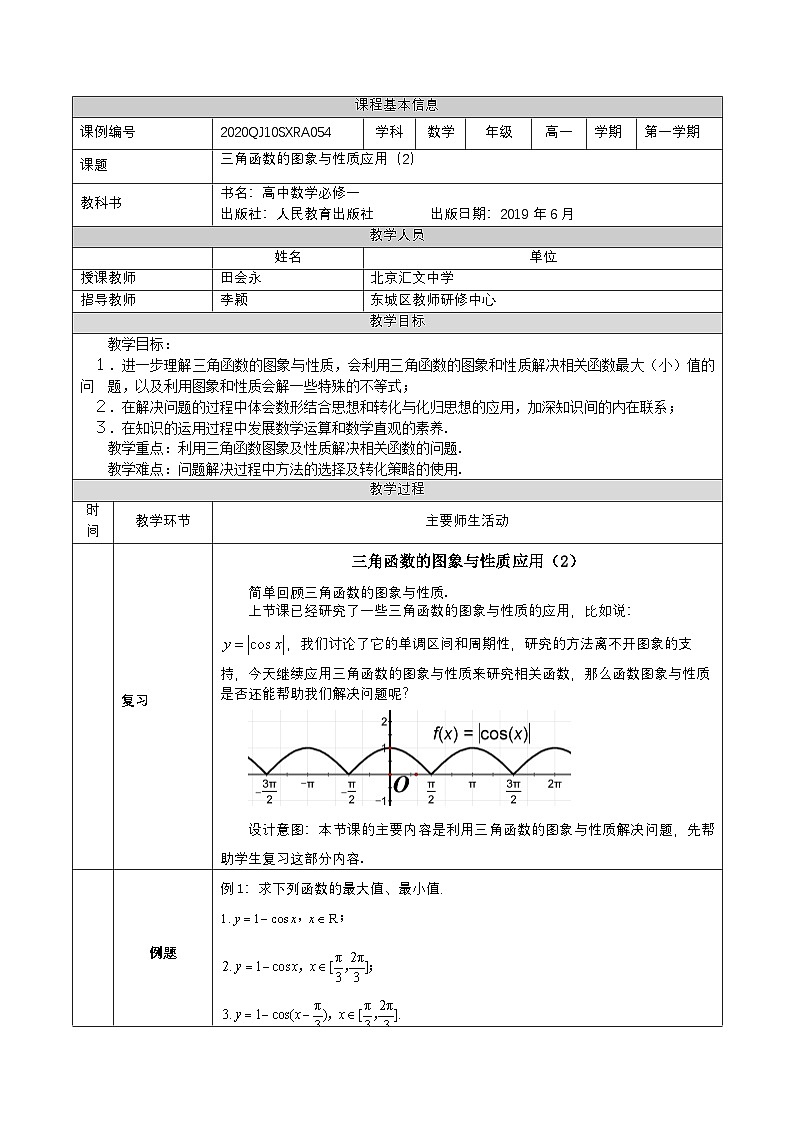
三角函数的图象与性质应用（2）
简单回顾三角函数的图象与性质.
上节课已经研究了一些三角函数的图象与性质的应用，比如说：，我们讨论了它的单调区间和周期性，研究的方法离不开图象的支持，今天继续应用三角函数的图象与性质来研究相关函数，那么函数图象与性质是否还能帮助我们解决问题呢？
设计意图：本节课的主要内容是利用三角函数的图象与性质解决问题，先帮助学生复习这部分内容.
例题
例1：求下列函数的最大值、最小值.
分析：
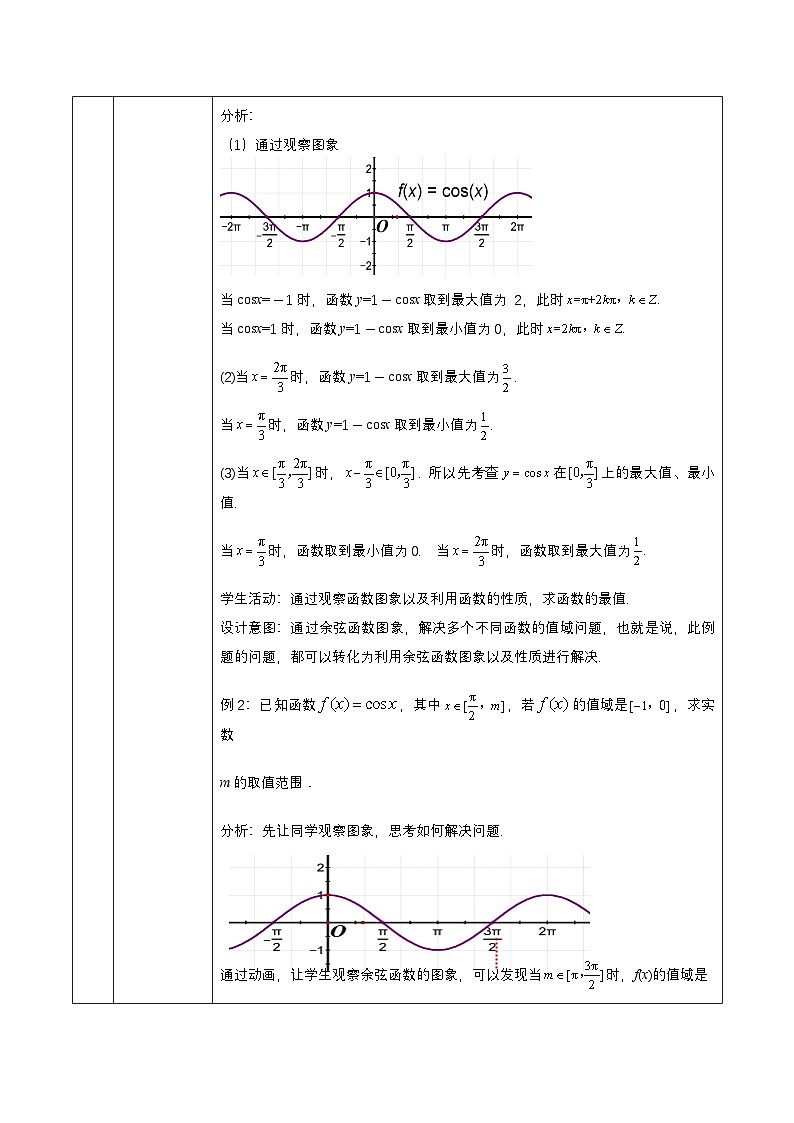
（1）通过观察图象
当csx=-1时，函数y=1-csx取到最大值为 2，此时
当csx=1时，函数y=1-csx取到最小值为0，此时
(2)当时，函数y=1-csx取到最大值为.
当时，函数y=1-csx取到最小值为
(3)当时，. 所以先考查在上的最大值、最小值.
当时，函数取到最小值为0. 当时，函数取到最大值为
学生活动：通过观察函数图象以及利用函数的性质，求函数的最值.
设计意图：通过余弦函数图象，解决多个不同函数的值域问题，也就是说，此例题的问题，都可以转化为利用余弦函数图象以及性质进行解决.
例2：已知函数，其中，若的值域是，求实数
m的取值范围．
分析：先让同学观察图象，思考如何解决问题.
通过动画，让学生观察余弦函数的图象，可以发现当时，f(x)的值域是
.
学生活动：观察图象，思考如何利用函数图象解决此问题.
设计意图：此题若通过代数方法解决是比较困难的，而利用图像，可以非常直观的展现出m的取值范围.
思考题1：已知函数，其中，若f(x)的值域是，
求m的取值范围．
当时，，接下来只需考察在上的
值域是. 这就转化为例2的情况.
在例2中，，所以此题的m满足：，解得：.
学生活动：同学们体会函数图象及性质在此题中的作用.
设计意图：与例2相比，此例题中的函数有一点变化，但任然可以使用三角函数图象及性质进行解决.
思考题2：已知函数，其中，若f(x)的值域是，
求m的取值范围．
分析：当时，，接下来只需只需在
的值域是这个问题. 这就转化为例2的情况. 在例2中，
，所以此题的m满足：，解得：.
学生活动：让同学体会函数图象及性质在此题中的作用，并思考与前面两个例题的关系.
设计意图：与前面两个题相比，此例题中的函数又有一点变化，但任然可以使用三角函数图象及性质进行解决.
例3：求不等式的解集.
分析：通过观察正、余弦函数的图象，先计算出的解，进而得到不等式在内的解. 在内，不等式的解集为：.
因此，不等式的解集为：
学生活动：有些学生可能会使用代数方法进行解决，但借助函数图形，可以相对轻松的解决此问题，让学生思考，函数图形及性质在此题中的作用.
设计意图：利用三角函数图形及性质解不等式.
思考题：求不等式的解集.
分析：不等式可转化为：.

在内，的解为.
的解为.
因此在R上，的解集为
小结
利用三角函数图象及性质研究函数的值域；
利用三角函数图象及性质研究一些不等式的解集.