浙教版（2024）九年级上册4.1 比例线段完美版ppt课件

这是一份浙教版（2024）九年级上册4.1 比例线段完美版ppt课件，共28页。PPT课件主要包含了x21，x12±1，x210，巴特农神庙，芭蕾舞等内容，欢迎下载使用。
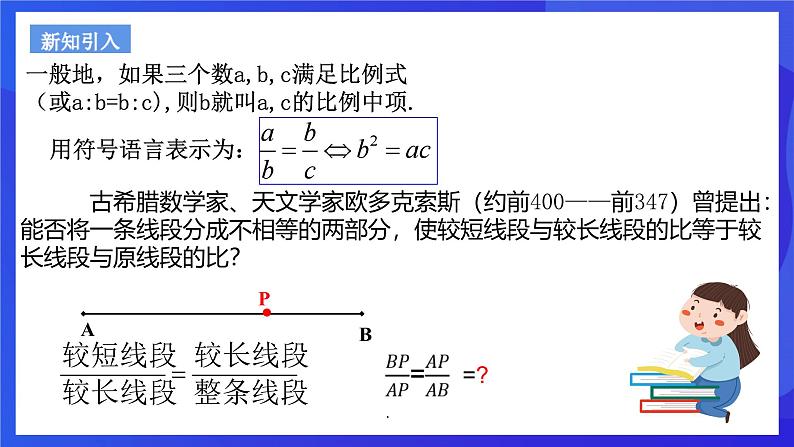
古希腊数学家、天文学家欧多克索斯（约前400——前347）曾提出：能否将一条线段分成不相等的两部分，使较短线段与较长线段的比等于较长线段与原线段的比？
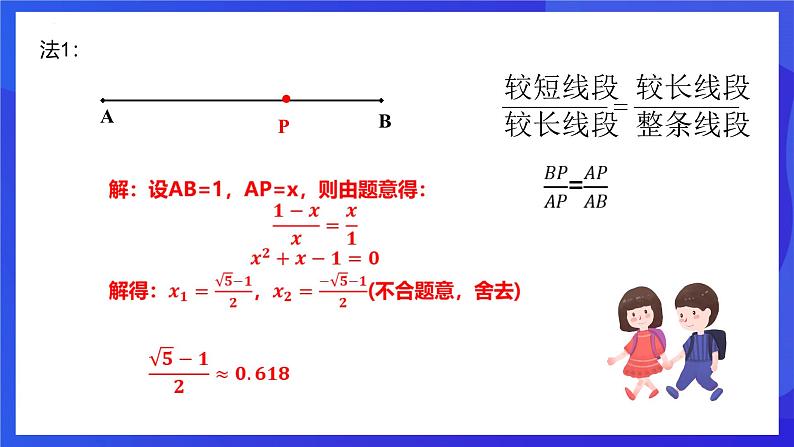
设ＡＢ＝a,　AP=x
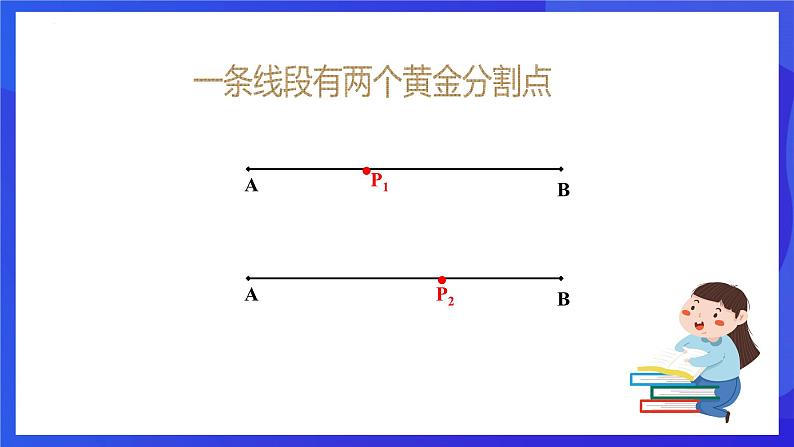
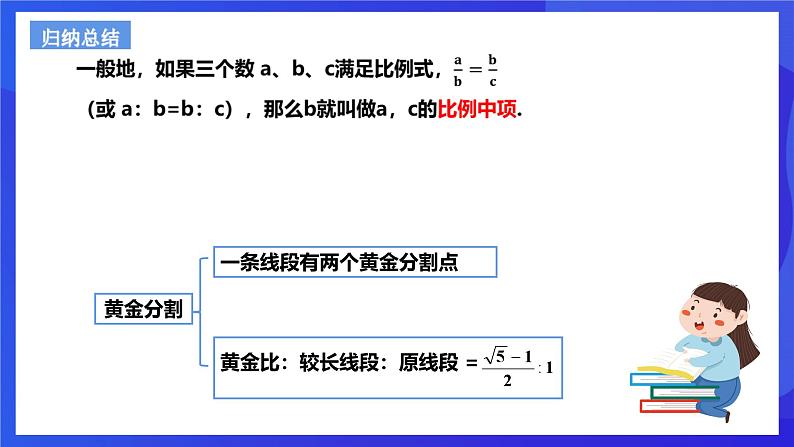
一条线段有两个黄金分割点
注意：线段的比例中项是一个正数，而数的比例中项是一对相反数
著名画家达•芬奇的名画＜蒙娜丽莎＞，画中脸部被围在矩形ＡＢＣＤ中，图中四边形ＢＣＥＦ为正方形，而在线段上的点Ｆ把线段分成两条线段，其中
世界艺术珍品——维纳斯女神，她是公元前一百多年希腊雕塑鼎盛时期的代表作，她的上半身和下半身的比值接近0.618.
若矩形的宽与长的比约为0.618,这样的矩形称之为黄金矩形.
你知道芭蕾舞演员跳舞时为什么要掂起脚尖吗?
芭蕾舞演员的身段是苗条的，但下半身与身高的比值也只有0.58左右，演员在表演时掂起脚尖，身高就可以增加6-8cm.这时比值就接近0.618了,给人以更为优美的艺术形象.
勾股定理和黄金分割是几何中的双宝,“前者好似黄金，后者堪称珠玉”。
蝴蝶身长与双翅展开后的长度之比, 接近0.618; 节目主持人报幕，绝对不会站在舞台的中央，而总是站在舞台的1／3处，站在舞台上侧近于0.618的位置才是最佳的位置;
1.人体肚脐不但是美化身型的黄金点有时还是医疗效果黄金点，许多民间名医在肚脐上贴药治好了某些疾病。
2.人体最感舒适的温度是23℃，也是正常人体温（37℃）的黄金点（23=37×0.618）.
3.人体还有几个黄金点：肚脐上部分的黄金点在咽喉，肚脐以下部分的黄金点在膝盖，上肢的黄金点在肘关节。上肢与下肢长度之比均近似0.618.
解：因为点P是线段AB的黄金分割点，且AP>PB
1.上海东方明珠电视塔高468m,上球体是塔身的黄金分割点,它到塔底部的距离大约是多少米(精确到0.1m)?
468×0.618≈289.2m
360×0.382=137.52
4．如图，已知P是线段AB的黄金分割点，且PA＞PB，若S1表示以PA为一边的正方形的面积，S2表示长是AB，宽是PB的矩形的面积，则S1____S2.(填“＞”“＝”或“＜”)
5.作顶角为36°的等腰△ABC;量出 底BC与腰AB的长度,计算: ; 作∠B的平分线,交AC于点D,量出CD的长度, 再计算: . (精确到0.001)
☆顶角为36°的等腰三角形称为 黄金三角形
☆点D是线段AC的黄金分割点.
☆再作∠C的平分线,交BD于E, △CDE也是黄金三角形……
6：已知线段AB=a，用直尺和圆规作出它的黄金分割点。
7.如图,正五边形ABCDE的5条边相等,5个内角也相等.⑴找找看,图中是否有黄金三角形?⑵点F是线段 的黄金分割点.
8、以长为2的线段AB为边作正方形ABCD，取AB的中点P，连接PD，在BA的延长线 上取点F，使PF=PD，以AF为边作正方形AMEF，点M在AD上． （1）求AM，DM的长； （2）点M是AD的黄金分割点吗？为什么？
黄金三角形：顶角为36°的等腰三角形(底与腰的比等于黄金数)；顶角为108°的等腰三角形(腰与底的比等于黄金数)．黄金矩形：宽与长的比等于黄金数的矩形．