浙教版数学九年级上册第三章《圆的基本性质章末复习----对角互补,四点共圆》 课件

这是一份浙教版数学九年级上册第三章《圆的基本性质章末复习----对角互补,四点共圆》 课件，共20页。
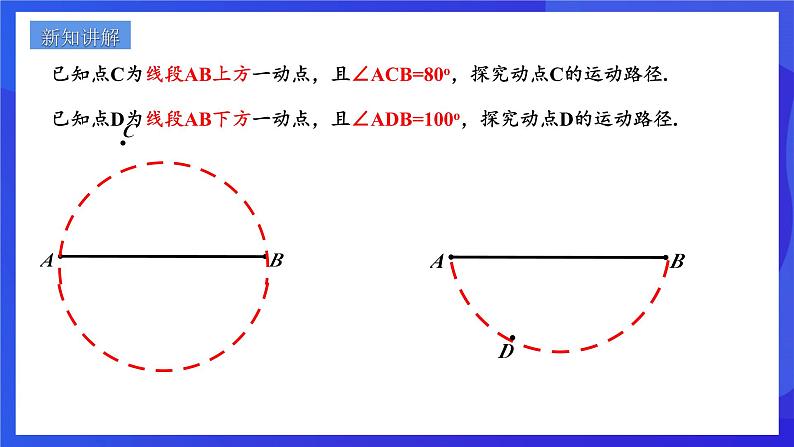
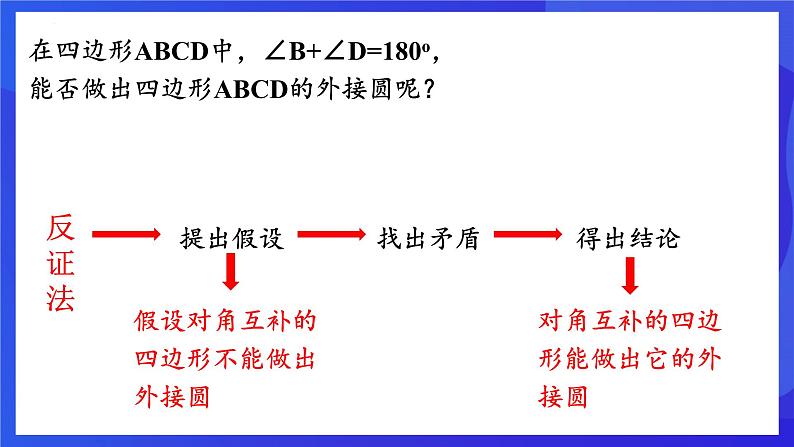
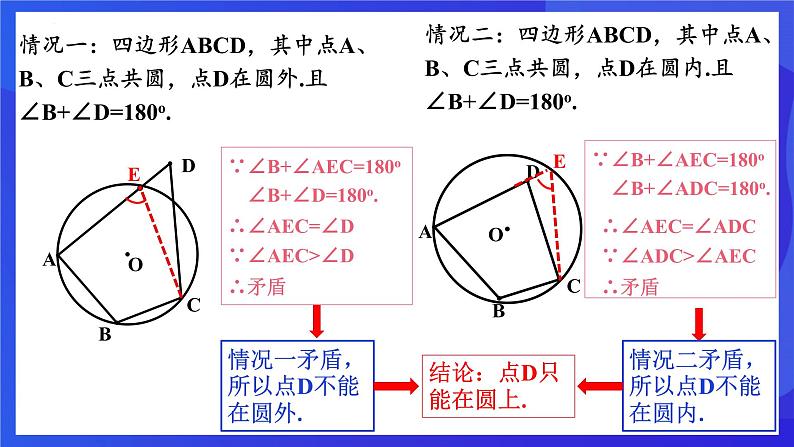
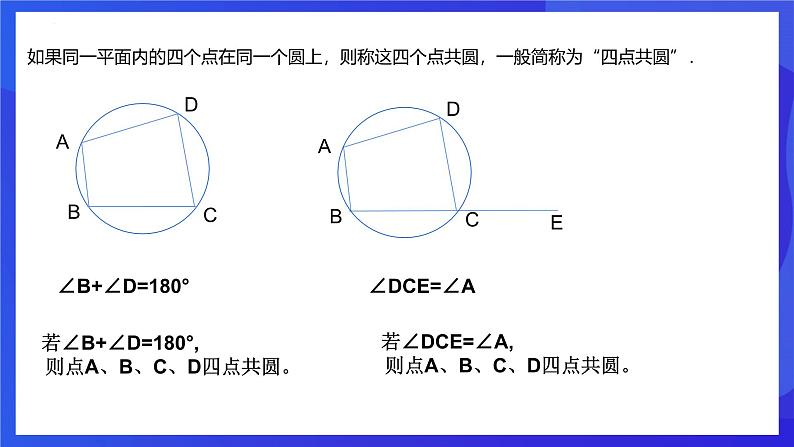
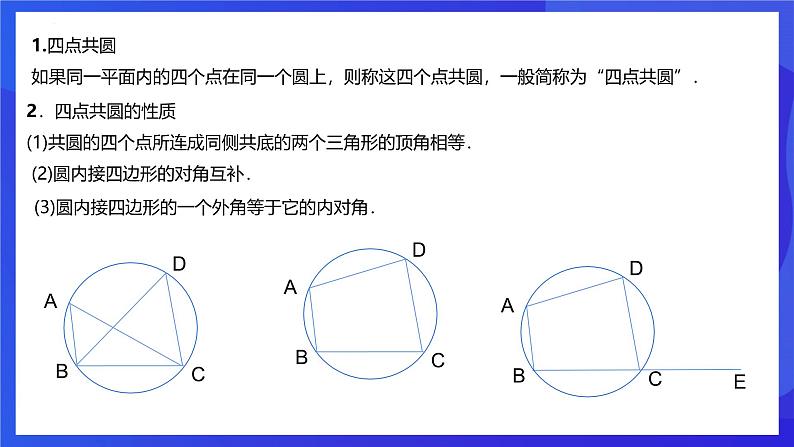
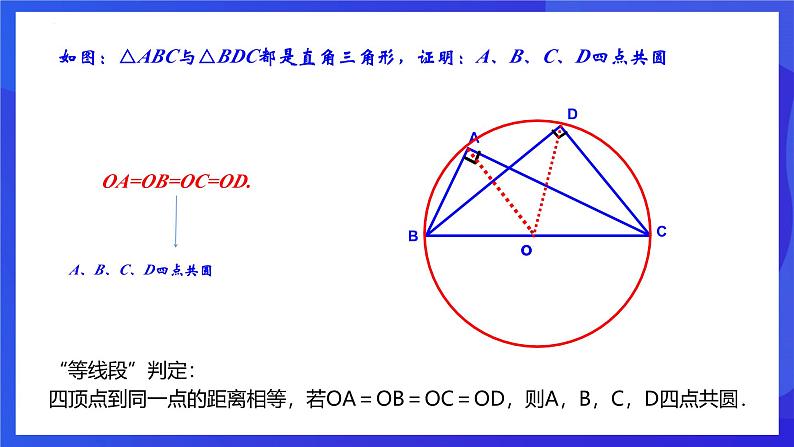
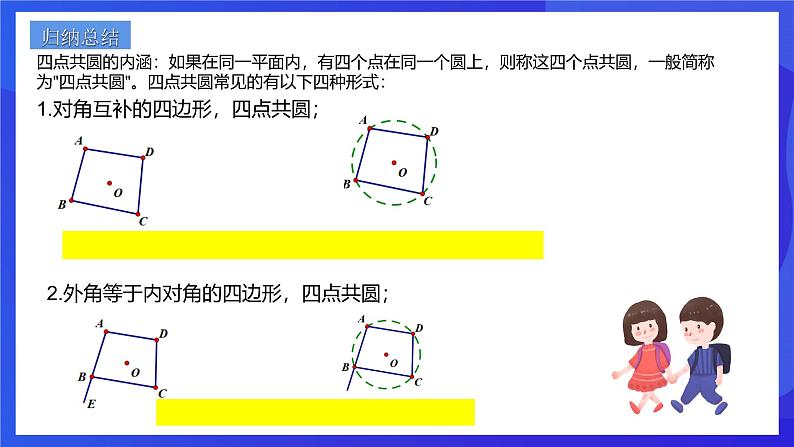
第三章 圆的基本性质章末复习 对角互补 已知点C为线段AB上方一动点，且∠ACB=80o，探究动点C的运动路径.已知点D为线段AB下方一动点，且∠ADB=100o，探究动点D的运动路径.新知讲解在四边形ABCD中，∠B+∠D=180o，能否做出四边形ABCD的外接圆呢？反证法提出假设假设对角互补的四边形不能做出外接圆找出矛盾得出结论对角互补的四边形能做出它的外接圆情况一：四边形ABCD，其中点A、B、C三点共圆，点D在圆外.且∠B+∠D=180o.O∵∠B+∠AEC=180o ∠B+∠D=180o.∴∠AEC=∠D ∵∠AEC>∠D ∴矛盾情况一矛盾，所以点D不能在圆外.情况二：四边形ABCD，其中点A、B、C三点共圆，点D在圆内.且∠B+∠D=180o.OE∵∠B+∠AEC=180o ∠B+∠ADC=180o.∴∠AEC=∠ADC∵∠ADC>∠AEC∴矛盾情况二矛盾，所以点D不能在圆内.结论：点D只能在圆上. 若∠B+∠D=180°, 则点A、B、C、D四点共圆。 如果同一平面内的四个点在同一个圆上，则称这四个点共圆，一般简称为“四点共圆”．∠B+∠D=180°∠DCE=∠A 若∠DCE=∠A, 则点A、B、C、D四点共圆。 1.四点共圆如果同一平面内的四个点在同一个圆上，则称这四个点共圆，一般简称为“四点共圆”．2．四点共圆的性质(1)共圆的四个点所连成同侧共底的两个三角形的顶角相等．(2)圆内接四边形的对角互补．(3)圆内接四边形的一个外角等于它的内对角．如图：△ABC与△BDC都是直角三角形，证明：A、B、C、D四点共圆OA=OB=OC=OD.A、B、C、D四点共圆“等线段”判定：四顶点到同一点的距离相等，若OA＝OB＝OC＝OD，则A，B，C，D四点共圆．四点共圆的内涵：如果在同一平面内，有四个点在同一个圆上，则称这四个点共圆，一般简称为"四点共圆"。四点共圆常见的有以下四种形式： 2.外角等于内对角的四边形，四点共圆；1.对角互补的四边形，四点共圆； 归纳总结 4.到定点的距离等于定长的四个点，四点共圆。 3.同底同侧的顶角相等的两个三角形，四点共圆； 1、在（1）矩形、（2）平行四边形、（3）等腰梯形、（4）菱形中能过四个顶点作圆的有__________________.（1） 、（3）当堂检测2.若EA·ED=EB·EC,则点A、B、C、D四点共圆。 EA·ED=EB·EC  ∠E=∠E△EAB∽△ECD∠ECD=∠A点A、B、C、D四点共圆3. AD、BE、CF是△ABC的三条高，相交于垂心H， 在A、B、C、D、E、F、H七点中，有几组四点共圆，试逐一举出， 并问各圆心在何处？  OC=OA=2 5.　如图，正方形ABCD，点O是对角线AC，BD的交点，点E在CD上,过点C作CF⊥BE，垂足为F，连接OF，求∠OFB的度数．┛┛┛┛450450∠OFB=4506．如图，在四边形ABCD中，∠ABC＝∠ADC＝90°，∠ABD＝72°，求∠CAD的度数解：∵∠ABC＝∠ADC＝90°，∴点A，点B，点C，点D四点共圆，∴∠ABD＝∠ACD＝72°，∴∠CAD＝90°﹣∠ACD＝18°，同斜边的直角三角形四点共圆。7．如图，AB是Rt△ABC和Rt△ABD的公共斜边，AC=BC，∠BAD=320，E是AB的中点，联结DE、CE、CD，求∠ECD的度数解：∵AB是Rt△ABC和Rt△ABD的公共斜边， E是AB中点，∴AE=EB=EC=ED，∴A、C、B、D在以E为圆心的圆上，∵∠BAD=32°，∴∠DCB=∠BAD=32°，又∵AC=BC，E是Rt△ABC的中点，∴∠ECB=45°，∴∠ECD=∠ECB-∠DCB=13°．3203208．如图所示，正方形ABCD中，BD为对角线，点E为BD上一点，过E作EF⊥AE，交DC于F，求证：AE=FE解：在正方形ABCD中，∠ADC=90°,∠BDC=45°∵EF⊥AE∴∠AEF=90°∴∠ADC+∠AEF=180°,A,E,F,D共圆，∴∠EAF=∠BDC=45°，∴∠EAF=∠EFA=45°,AE=EF.4504509．如图所示，在平行四边形ABCD中，点E为AB，BC的垂直平分线的交点，若∠D=600，求∠AEC. “圆”来如此简单！“圆”来如此美妙！“圆”汁“圆”味！有“圆”千里来相会！无“圆”对面不相逢！“圆”形必漏！“圆”木求鱼！“圆”“圆”不断！“圆”来是你！课程结束