浙教版（2024）七年级下册（2024）1.3 平行线习题

这是一份浙教版（2024）七年级下册（2024）1.3 平行线习题，共8页。
①任意两条直线的位置关系不是相交就是平行
②过一点有且只有一条直线和已知直线平行
③过两条直线a，b外一点P，画直线c，使c∥a，且c∥b
④若直线a∥b，b∥c，则c∥a．
A．4B．3C．2D．1
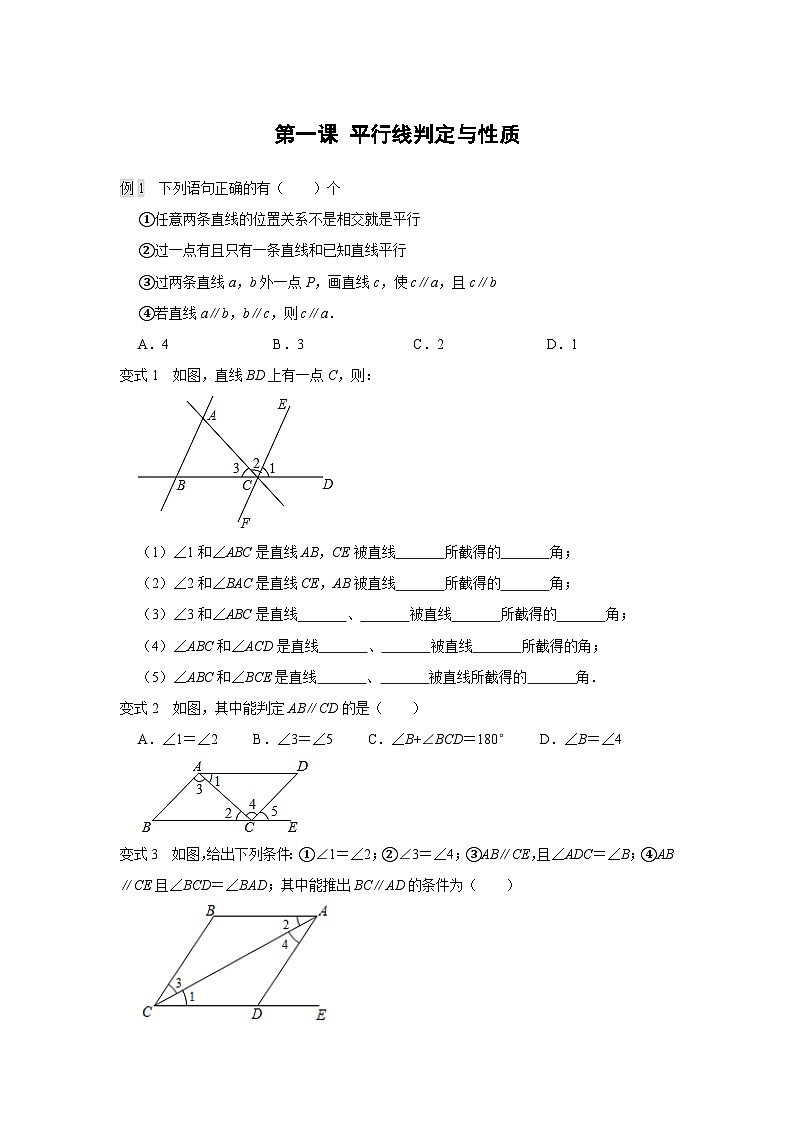
变式1 如图，直线BD上有一点C，则：
（1）∠1和∠ABC是直线AB，CE被直线 所截得的 角；
（2）∠2和∠BAC是直线CE，AB被直线 所截得的 角；
（3）∠3和∠ABC是直线 、 被直线 所截得的 角；
（4）∠ABC和∠ACD是直线 、 被直线 所截得的角；
（5）∠ABC和∠BCE是直线 、 被直线所截得的 角．
变式2 如图，其中能判定AB∥CD的是（ ）
A．∠1＝∠2 B．∠3＝∠5 C．∠B+∠BCD＝180° D．∠B＝∠4
变式3 如图，给出下列条件：①∠1＝∠2；②∠3＝∠4；③AB∥CE，且∠ADC＝∠B；④AB∥CE且∠BCD＝∠BAD；其中能推出BC∥AD的条件为（ ）
A．①②B．②④C．②③D．②③④
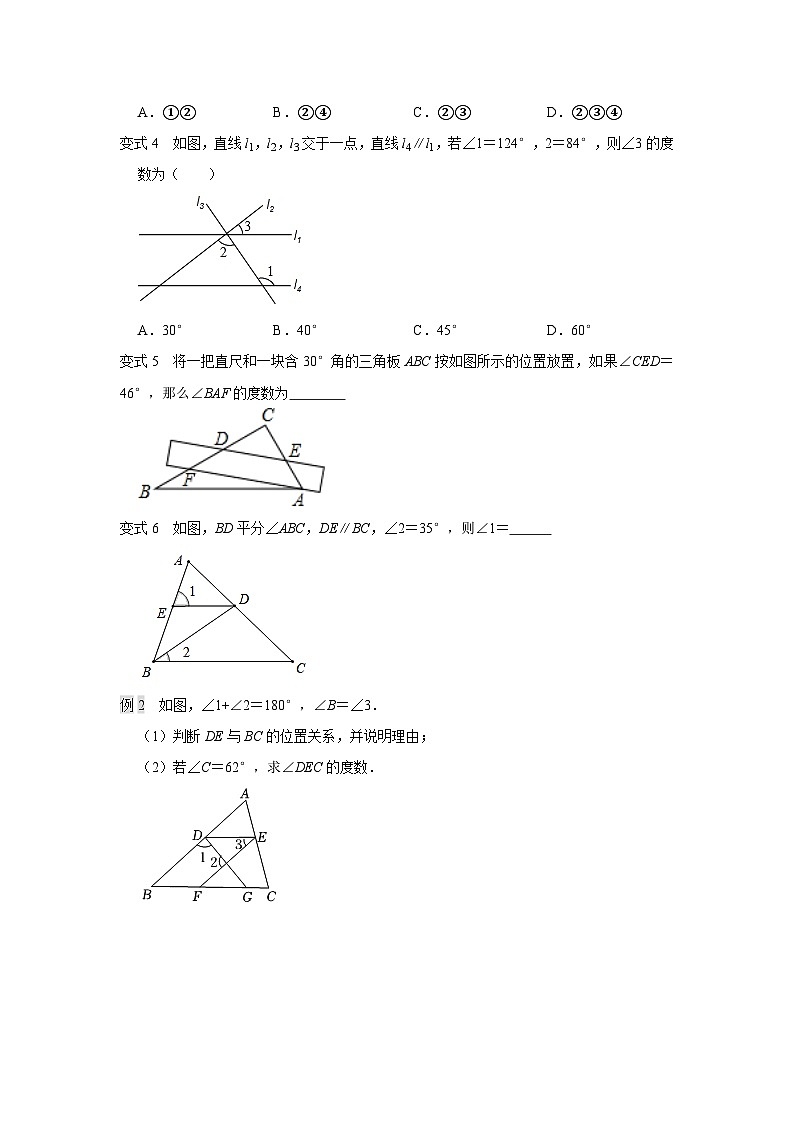
变式4 如图，直线l1，l2，l3交于一点，直线l4∥l1，若∠1＝124°，2＝84°，则∠3的度数为（ ）
A．30°B．40°C．45°D．60°
变式5 将一把直尺和一块含30°角的三角板ABC按如图所示的位置放置，如果∠CED＝46°，那么∠BAF的度数为
变式6 如图，BD平分∠ABC，DE∥BC，∠2＝35°，则∠1＝
例2 如图，∠1+∠2＝180°，∠B＝∠3．
（1）判断DE与BC的位置关系，并说明理由；
（2）若∠C＝62°，求∠DEC的度数．
变式1 如图，点D在AC上，点F、G分别在AC、BC的延长线上，CE平分∠ACB并交BD于H，且∠EHD+∠HBF＝180°．
（1）若∠F＝30°，求∠ACB的度数；
（2）若∠F＝∠G，求证：DG∥BF．
例3 已知：点A在射线CE上，∠C＝∠D．
（1）如图1，若AC∥BD，求证：AD∥BC；
（2）如图2，若∠BAC＝∠BAD，BD⊥BC，请探究∠DAE与∠C的数量关系，写出你的探究结论，并加以证明；
（3）如图3，在（2）的条件下，过点D作DF∥BC交射线于点F，当∠DFE＝8∠DAE时，求∠BAD的度数．
变式1 已知：如图，射线CB∥OA，∠C＝∠OAB＝120°，OE平分∠COF 交BC于点E，F在BC上，且满足OB平分∠AOF．
（1）求：∠EOB的度数．
（2）探究∠OBC与∠OFC的数量关系，并证明；若向右平移AB，则∠OBC与∠OFC的数量关系是否会发生变化？若发生变化，请直接写出变化的结论．
（3）在向右平移AB的过程中，能否使∠OEC＝∠OBA？若存在，求出此时两角相等的度数；若不存在，请说明理由．
补充练习
如图，已知∠1＝∠2，∠A＝∠D．
（1）判断AB与CD的位置关系，并说明理由；
（2）若∠B＝40°，求∠C的度数．
如图1所示，在四边形ABCD中，∠A＝∠C，点E在AB边上，DE平分∠ADC，且
∠ADE＝∠DEA．
（1）求证：AD∥BC；
（2）如图2，已知DF⊥BC交BC边于点G，交AB边的延长线于点F，且DB平分∠EDF．若∠BDC＝30°，求∠F与∠EDF的度数．
将一副三角板中的两块直角三角尺的顶点C按如图方式叠放在一起，其中∠A＝30°，∠ACB＝60°；∠E＝∠ECD＝45°，且B、C、D三点在同一直线上．现将三角板CDE绕点C沿顺时针方向旋转α度．
（1）当α＝0°时，∠ACE的度数为 ；
（2）当0°＜α＜360°时，若△CDE和△ABC有两组边互相平行，则α度数为 ；
（3）当0°＜α＜360°时，若△CDE和△ABC只有一组边互相平行，求α的度数．
如图，已知AM∥BN，∠B＝40°，点P是射线BN上一动点（与点B不重合），AC、AD分别平分∠BAP和∠PAM，交射线BN于点C、D．
（1）求∠CAD的度数；
（2）当点P运动时，∠APB与∠ADB之间存在怎样的数量关系？说明理由；
（3）当点P运动到使∠ACB＝∠BAD时，求∠BAC的度数．