数学八年级下册2. 矩形的判定教案配套ppt课件

这是一份数学八年级下册2. 矩形的判定教案配套ppt课件，共12页。
能应用矩形的判定解答简单的证明题和计算题.(难点)
知识点 矩形的性质与判定的综合应用
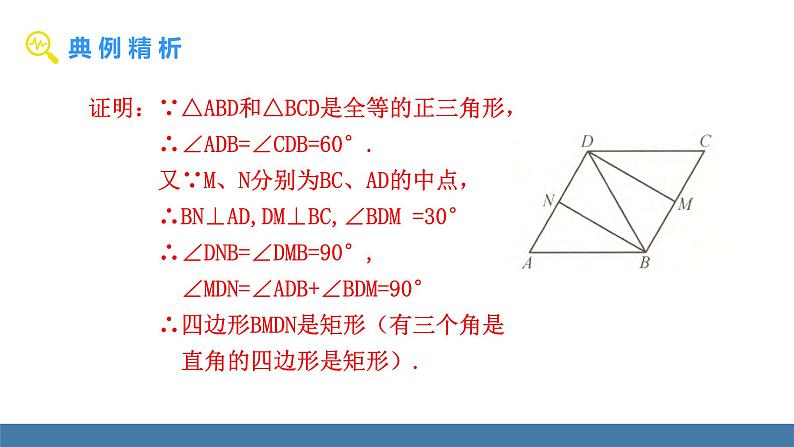
例1 如图，四边形ABCD是由两个全等的正三角形ABD和BCD组成的，M、N分别为BC、AD的中点.求证：四边形BMDN是矩形.
分析 由已知条件，可知BN⊥AD，DM⊥BC，因此，在四边形BMDN中，已有两个角是直角，只需再证明另一个角也是直角即可得到它是一个矩形.
证明：∵△ABD和△BCD是全等的正三角形， ∴∠ADB=∠CDB=60°. 又∵M、N分别为BC、AD的中点， ∴BN⊥AD,DM⊥BC,∠BDM =30° ∴∠DNB=∠DMB=90°, ∠MDN=∠ADB+∠BDM=90° ∴四边形BMDN是矩形（有三个角是 直角的四边形是矩形）.
例2 如图，在△ABC中，AB＝AC，AD⊥BC，垂足为点D，AE是△BAC的外角平分线，DE∥AB交AE于点E，求证：四边形ADCE是矩形．
又∵AE∥DC，∴四边形ADCE是平行四边形，∴四边形ADCE是矩形(对角线相等的平行四边形是矩形).
☀归纳 判定一个四边形是矩形时，要结合条件灵活选择方法．如果可以证明三个角是直角，可直接证出矩形；如果只能证出一个角是直角或对角线相等，可以先尝试证出这个四边形是平行四边形．
1.下列各句判定矩形的说法是否正确？
（1）对角线相等的四边形是矩形；
（2）对角线互相平分且相等的四边形是矩形；
（3）有一个角是直角的四边形是矩形；
（5）有三个角是直角的四边形是矩形；
（6）四个角都相等的四边形是矩形；
（7）对角线相等，且有一个角是直角的四边形是矩形；
（4）有三个角都相等的四边形是矩形;
（8）一组对角互补的平行四边形是矩形.
证明：∵四边形ABCD为平行四边形， ∴AO＝OC，OD＝OB.∵AN＝CM，ON＝OB，∴ON＝OM＝OD＝OB，∴四边形NDMB为平行四边形，MN＝BD， ∴▱NDMB为矩形．
2.如图，▱ABCD中，对角线AC、BD相交于点O，延长OA到N，使ON＝OB，再延长OC至M，使CM＝AN.求证：四边形NDMB为矩形．
3.如图，在△ABC中，AB＝AC，AD⊥BC，垂足为D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为E，求证：四边形ADCE为矩形．
能力提升：4.如图，在梯形ABCD中，AD∥BC，∠B＝90°，AD＝24cm，BC＝26cm，动点P从点A出发沿AD方向向点D以1cm/s的速度运动，动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动．点P、Q分别从点A和点C同时出发，当其中一点到达端点时，另一点随之停止运动．(1)经过多长时间，四边形PQCD是平行四边形？(2)经过多长时间，四边形PQBA是矩形？
(1)解：设经过xs，四边形PQCD为平行四边形， 即PD＝CQ， ∴24－x＝3x， 解得x＝6.∴经过6s，四边形PQCD是平行四边形；
(2)经过多长时间，四边形PQBA是矩形？
(2)解：设经过ys，四边形PQBA为矩形，即AP＝BQ，所以y＝26－3y，解得y＝6.5，即经过6.5s，四边形PQBA是矩形．