

高中数学人教A版 (2019)选择性必修 第一册3.3 抛物线教案
展开
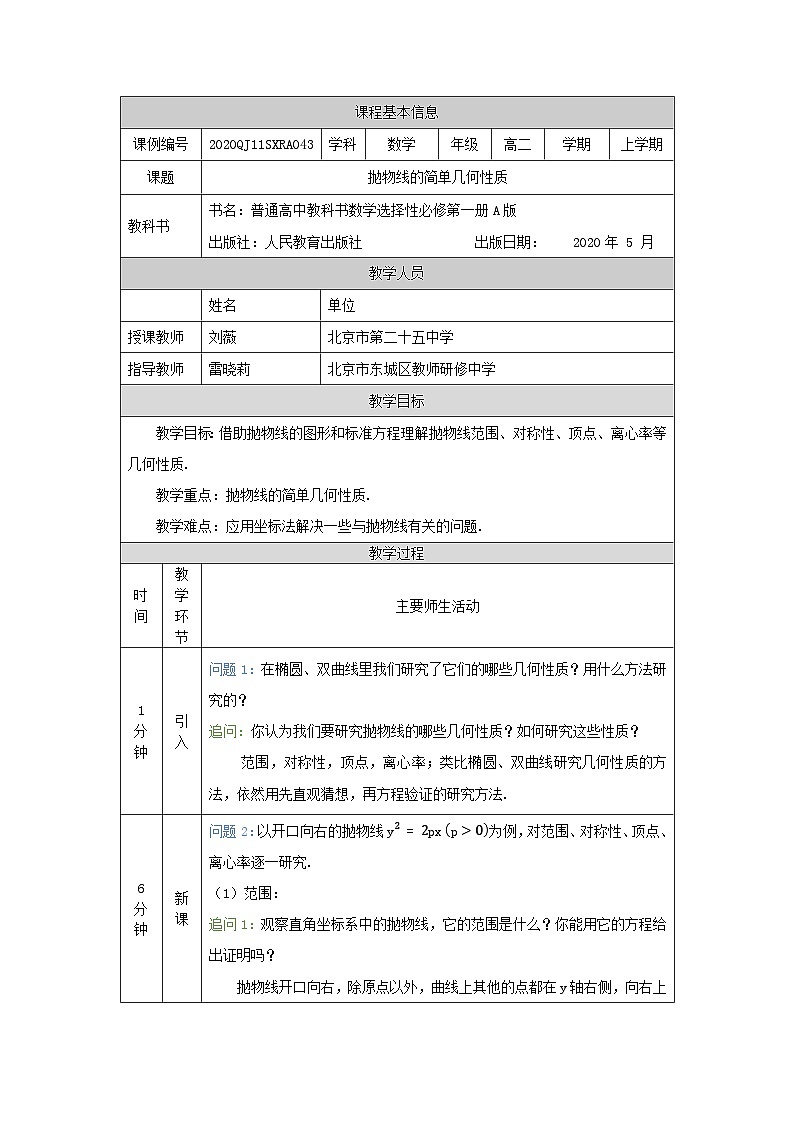
这是一份高中数学人教A版 (2019)选择性必修 第一册3.3 抛物线教案,共6页。
课例编号
2020QJ11SXRA043
学科
数学
年级
高二
学期
上学期
课题
抛物线的简单几何性质
教科书
书名:普通高中教科书数学选择性必修第一册A版
出版社:人民教育出版社 出版日期: 2020年 5 月
教学人员
姓名
单位
授课教师
刘薇
北京市第二十五中学
指导教师
雷晓莉
北京市东城区教师研修中学
教学目标
教学目标:借助抛物线的图形和标准方程理解抛物线范围、对称性、顶点、离心率等几何性质.
教学重点:抛物线的简单几何性质.
教学难点:应用坐标法解决一些与抛物线有关的问题.
教学过程
时间
教学环节
主要师生活动
1
分钟
引入
问题1:在椭圆、双曲线里我们研究了它们的哪些几何性质?用什么方法研究的?
追问:你认为我们要研究抛物线的哪些几何性质?如何研究这些性质?
范围,对称性,顶点,离心率;类比椭圆、双曲线研究几何性质的方法,依然用先直观猜想,再方程验证的研究方法.
6
分钟
新课
问题2:以开口向右的抛物线 y2=2px p>0为例,对范围、对称性、顶点、离心率逐一研究.
(1)范围:
追问1:观察直角坐标系中的抛物线,它的范围是什么?你能用它的方程给出证明吗?
抛物线开口向右,除原点以外,曲线上其他的点都在 y 轴右侧,向右上方和右下无限延伸.
从方程 y2=2px p>0 可知,因为 p>0 ,等号左边是完全平方,所以对于抛物线上的点 Mx,y ,都有,;当的值增大时,y的值也增大,这说明抛物线向右上方和右下方无限延展.
(2)对称性:
追问2:观察方程 y2=2px p>0的曲线,开口向右的抛物线有对称轴、对称中心么?类比椭圆、双曲线对称性的证明,你能从抛物线的方程入手,给出证明吗?
由图象可知,方程 y2=2px p>0的曲线关于x 轴对称,没有对称中心.以 -y 代替 y ,我们发现方程 y2=2px p>0 不变,所以抛物线关于 x 轴对称. 我们把抛物线的对称轴叫做抛物线的轴.
(3)顶点:
追问3:椭圆、双曲线的顶点如何定义的?
曲线与对称轴的交点叫做曲线的顶点,所以椭圆有四个顶点,双曲线有两个顶点.
追问4:抛物线有几个顶点?能证明吗?
抛物线与对称轴交于原点,从方程来看,当 x=0 时,y=0 ,因此,抛物线只有一个顶点,就是原点0 , 0.
(4)离心率:
它的定义是:抛物线上的点 M 与焦点 F 的距离和点 M 到准线的距离 d 的比,叫做抛物线的离心率,用 e 表示. 由抛物线的定义可知,e=1.
另几种开口方向的抛物线的性质,请同学们用同样的方法探究一下.
13
分钟
知识应用
问题3:已知抛物线关于 x 轴对称,它的顶点在原点,并且经过点M2,-22,求它的标准方程.
追问1:根据给定的条件,怎么求抛物线的标准方程?
根据待定系数法,设抛物线的方程,代入经过的点 M 的坐标就可以确定系数 p 的值.
追问2:此题选择哪种抛物线的标准方程呢?
由于抛物线关于x 轴对称,顶点在原点,经过的 M 点在第四象限,所以可以判定抛物线开口向右,焦点在x 轴的正半轴上,所以设它的标准方程为
y2=2px p>0.
因为点 M 在抛物线上,所以代入坐标,得
-222=2p×2 p>0
解得 p=2.
因此,所求抛物线的标准方程是
y2=4x.
追问3:如果把条件“关于 x 轴对称”改为“对称轴是坐标轴”,那么结果有变化吗?
点 M 在第四象限,那么抛物线除了关于 x 轴对称,还可以关于 y 轴对称,即开口向下.
此时,设标准方程为 x2=2py p>0,同样采用待定系数法,代入点 M 的坐标,得 22=2p×-22 p>0,解得.因此,所求抛物线的标准方程是 x2=-2y.因此,如果条件“关于 x 轴对称”改为“对称轴是坐标轴”,那么结果有两个,分别是 y2=4x, x2=-2y.
小结:选择抛物线的标准方程是解题的关键点,所以在设方程之前,先确定抛物线的开口方向,而后,抛物线方程中只有一个待定系数 p ,所以只要一个条件就可以带入求值了.
问题4:斜率为1的直线 l 经过抛物线 y2=4x 的焦点 F ,且与抛物线相交于A,B 两点,求线段 AB 的长.
追问1:在前面椭圆、双曲线的学习中,我们也遇到过类似的直线与椭圆、双曲线相交的问题,回忆一下是如何解决的,对于这道题,你有什么解答思路?
解法一:可求得,直线 l 的方程为 y=x-1.
联立直线的方程与抛物线的方程,
y=x-1 , y2=4x .
整理得x2-6x+1=0.
用求根公式解得或
即A3+22,2+22,B3-22,2-22.
由两点间距离公式,得
AB=x2-x12+y2-y12
=3+22-3+222+2+22-2+222=8.
即线段AB的长为8.
小结:这种方法与之前直线与椭圆、双曲线相交问题上所使用的方法是统一的,说明它具有一般性,为我们解决直线与圆锥曲线问题提供了基本的解题思路. 但是在计算时有些麻烦.
追问2:能否不求出A,B两点的坐标而求出|AB|呢?
在两点间距离公式 AB=x2-x12+y2-y12 中,我们只要求出x2-x12,y2-y12的值就可以求出AB,由此得到解决这个问题的第二种方法.
解法二:设 Ax1,y1,Bx2,y2,将直线 l 的方程 y=x-1与抛物线的标准方程 y2=4x 联立,代入消元得 x2-6x+1=0 ,所以可得x1+x2=6,x1x2=1,
x2-x12=x1+x22-4x1x2=62-4×1=32.
因为 y1=x1-1,y2=x2-1, y2-y12=x2-x12=32.
所以,AB=x2-x12+y2-y12=32+32=8.
小结:相较第一种解法,应用一元二次方程根与系数关系,计算过程简化很多,所以在解决数学问题时,希望同学们多注意观察和思考,用最简便的方法解决问题.
追问3:根据题目条件作图观察,应用数形结合的思想,再回忆一下抛物线的定义,有没有给你一些启发?
解法三:直线 l 过抛物线的焦点,根据抛物线的定义可知,抛物线上的点到焦点的距离与该点到准线的距离相等,所以AF=AA',BF=BB'.那么
AB=AF+BF=AA'+BB',
因为轴,所以.
同理.
于是得, AB=AF+BF=AA'+BB'=x1+x2+p.
由题意知,p=2,再由解法二,联立直线 l 的方程与抛物线方程,代入化简得 x2-6x+1=0. 根据根与系数关系,得 x1+x2=6 .所以,
AB=x1+x2+p=6+2=8.
所以,线段 AB 的长是8.
追问4:如果直线 l 不经过焦点 F ,那么 AB 还等于 x1+x2+p 吗?
由图观察,显然
AF+BF=x1+p2+x2+p2=x1+x2+p> AB
所以,如果直线 l 不经过焦点 F ,那么 AB 不等于 x1+x2+p. 同学们也可以用代数法,设出直线 l 的方程,与抛物线方程联立,探究AB与谁的值有关,从而发现它的长度不是等于x1+x2+p .
小结:比较三种解题方法,可以发现这三种方法各有特点.解法一最直接,具有一般性,但是计算量大.解法二运用一元二次方程根与系数的关系,简化运算,但是需要掌握变形技巧.解法三充分运用抛物线的定义:抛物线上的点到焦点的距离等于这个点到准线的距离,使运算大大简化,但要注意,直线必须过焦点. 这种方法把抛物线的标准方程和其几何特征紧密地结合起来,体现了用坐标法解决问题的基本思想方法:先用几何眼光观察,再用代数运算解决.
2分钟
归纳小结
本课小结:
本节课我们研究了抛物线的哪些几何性质?
这些性质通过什么方法得到?直观猜想,方程验证.
直线与抛物线相交,用坐标法研究所得线段长的问题的一般思路与方法是什么?
1
分钟
课后作业
课后练习:
求适合下列条件的抛物线的标准方程:
关于 y 轴对称,准线经过点 E5,-5;
准线在 y 轴的右侧,顶点到准线的距离是4;
过点 M2,0 作斜率为1的直线 l ,交抛物线 y2=4x 于 A,B 两点,求AB.
相关教案
这是一份高中数学人教A版 (2019)选择性必修 第一册3.3 抛物线教案及反思,共6页。
这是一份数学选择性必修 第一册3.3 抛物线教学设计及反思,共7页。
这是一份高中数学人教A版 (2019)选择性必修 第一册第三章 圆锥曲线的方程3.2 双曲线教学设计及反思,共6页。









