人教版（2024）七年级下册（2024）7.1.3 两条直线被第三条直线所截教课内容课件ppt

这是一份人教版（2024）七年级下册（2024）7.1.3 两条直线被第三条直线所截教课内容课件ppt，共51页。PPT课件主要包含了学习目标，链接中考等内容，欢迎下载使用。
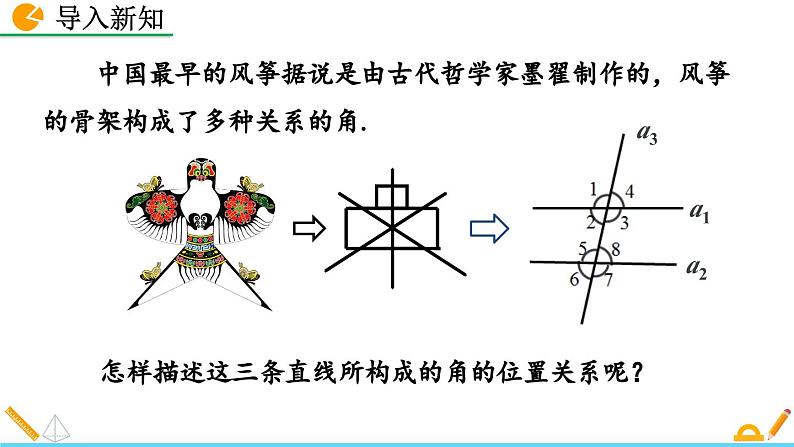
中国最早的风筝据说是由古代哲学家墨翟制作的，风筝的骨架构成了多种关系的角.
怎样描述这三条直线所构成的角的位置关系呢？
1. 了解同位角、内错角、同旁内角的概念.
2. 会在简单的图形中辨认同位角、内错角、同旁内角.
3. 会在给定某个条件下进行有关同位角、内错角、同旁内角的判定.
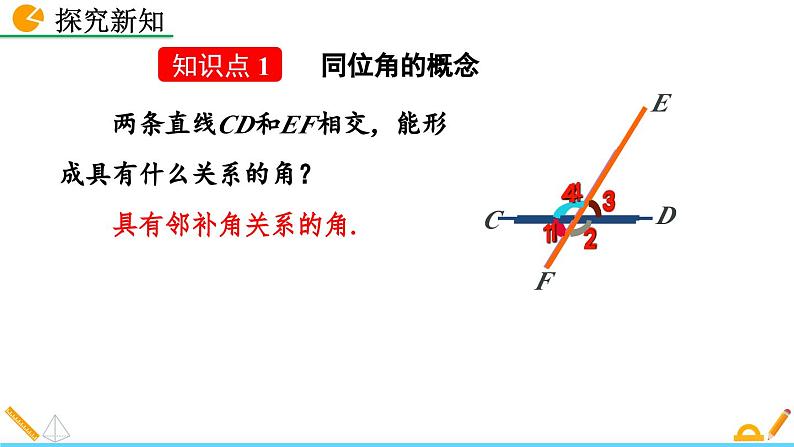
两条直线CD和EF相交，能形成具有什么关系的角？
两条直线CD和EF相交，还能形成具有什么关系的角？
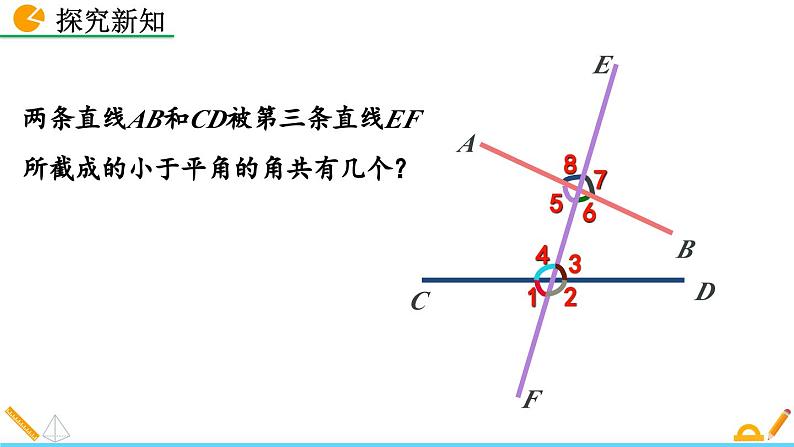
两条直线AB和CD被第三条直线EF所截成的小于平角的角共有几个？
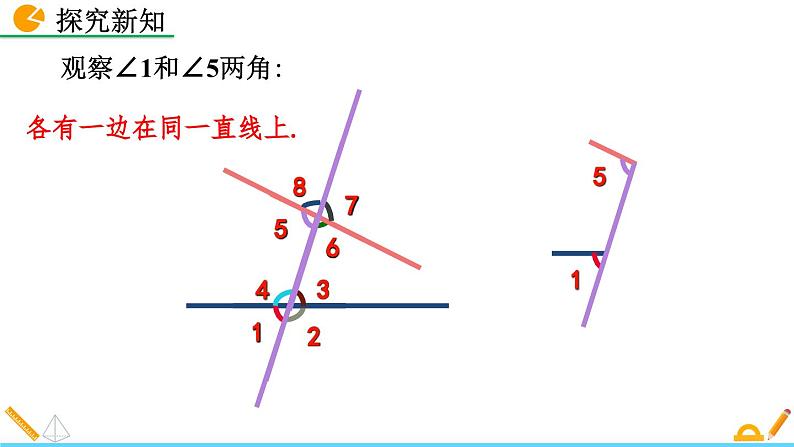
各有一边在同一直线上.
另一边在截线的同旁, 方向同向.
一边都在截线上而且同向，另一边在截线同侧的两个角.
分别在截线的左侧(同侧)在被截直线的下方(同方向)
图形特征：在形如字母“F”的图形中有同位角.
变式图形：图中的∠1与∠2都是同位角.
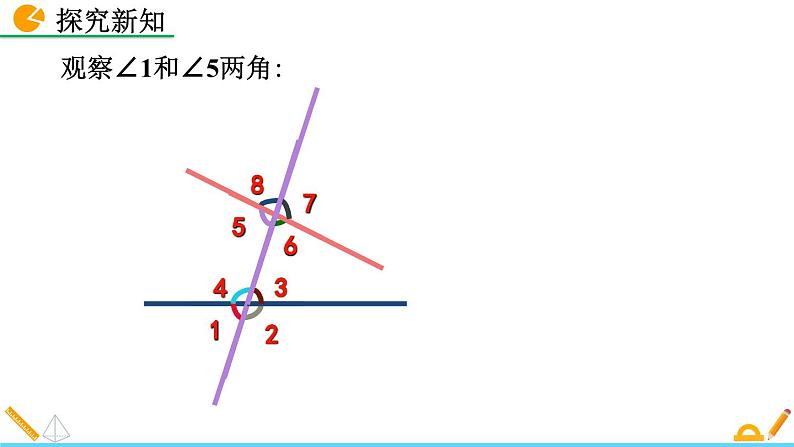
图中的同位角除∠1和∠5外，还有……
A.(1)，(2) B.(3)，(4) C.(1)，(2)，(3) D.(2)，(3) ，(3)
下列图形中，∠1和∠2是同位角的有（ ）
下列各图中∠1与∠2哪些是同位角？哪些不是？
归纳特征：两角的两边组成字母F.
另一边在截线的两侧, 方向相反.
一边都在截线上而且反向，另一边在截线两侧的两个角.
夹在两被截直线内,分别在截线两侧(交错).
变式图形：图中的∠1与∠2都是内错角.
图形特征：在形如“Z”的图形中有内错角.
图中的内错角除∠3和∠5外，还有……
如图，（1）∠1和∠4是直线____与直线____被直线______所截形成的__________.（2）∠2和∠3是直线_____与直线____被直线______所截形成的_______.
另一边在截线的同旁, 方向相同.
一边都在截线上而且反向，另一边在截线同旁的两个角.
在截线同旁,夹在两被截直线内.
变式图形：图中的∠1与∠2都是同旁内角.
图形特征：在形如“U”的图形中有同旁内角.　
如果把图看成是直线AB，EF被直线CD所截，那么∠1与∠2是一对什么角？
如图，直线DE,BC被直线AB所截. （1）∠1和∠2， ∠1和∠3，∠1和∠4各是什么位置关系的角？
解：（1）∠1和∠2是内错角，∠1和∠3是同旁内角，∠1和∠4是同位角.
提示：解题之前要明确哪两条直线被哪条直线所截.
解：（2）如果∠1=∠4， 由对顶角相等，得∠2=∠4，那么∠1=∠2.
（2）如果∠1=∠4，那么∠1与∠2相等吗？∠1与∠3互补吗？ 为什么？
因为∠3和∠4互补，即∠4+∠3=180°， 又因为∠1=∠4, 所以∠1+∠3=180°,即∠1与∠3互补.
分别指出下列各图中的同位角、内错角 、同旁内角.
解：（1）同位角：∠1与∠5，∠2与∠6，∠3与∠7，∠4与∠8；
内错角： ∠3与∠5，∠4与∠6；
同旁内角：∠3与∠6 ，∠4与∠5.
解：（2）同位角：∠1与∠3，∠2与∠4；
同旁内角：∠2与∠3.
如图，直线DE截AB ，AC，构成8个角，指出所有的同位角,内错角,同旁内角.
解：被截线是AB，AC，截线是DE，所以8个角中，
在复杂图形中识别同位角、内错角、同旁内角
同位角：∠2与∠5，∠4与∠7，∠1与∠8, ∠6与∠3；
内错角：∠4与∠5，∠1与∠6；
同旁内角：∠1与∠5，∠4与∠6.
1.识别这些角是同位角、内错角还是同旁内角.
2.如图，∠B与哪个角是内错角？与哪个角是同旁内角？它们分别是哪两条直线被哪一条直线所截形成的？对∠C进行同样的讨论.
解:∠B与∠DAB是内错角, ∠ B与∠BAE是同旁内角,是直线DE 和 BC被直线 AB 所截形成的; ∠ B与∠BAC是同旁内角,是直线AC 和BC被直线 AB 所截形成的; ∠B与∠C是同旁内角,是直线AB和AC被直线 CB 所截形成的.
2.如图，∠B与哪个角是内错角？与哪个角是同旁内角？它们分别是哪两条直线哪一条直线所截形成的？对∠C进行同样的讨论.
解: ∠ C与∠EAC是内错角, ∠ C与∠DAC 是同旁内角,是直线DE 和 BC 被直线AC所截形成的; ∠C与∠BAC是同旁内角,是直线AB 和 BC被直线AC 所截形成的; ∠C与∠B是同旁内角,是直线AB 和AC 被直线CB 所截形成的.
如图，∠B的同位角可以是（　　） A．∠1 B．∠2 C．∠3 D．∠4
1.如图，∠DAB和∠ABC的位置关系是( ） A.同位角 B.同旁内角 C.内错角 D.以上结论都不对
2.如图，∠1和∠2不能构成同位角的图形是（ ）
A B C D
3.看图填空：
（1）如图1所示，若ED，BF被AB所截，则∠1与_____是同位角.
(2)如图2,∠1与∠3是AB和AF被_____所截构成的 角；
(3)如图3,∠2与∠4是 和 被BC所截构成的_____角.
学校与游乐场所在的角形成一对（　　　）角;学校与超市所在的角形成一对（　　　　）角;学校与飞机场所在的角形成一对（　　　）角.
∠A与∠8是哪两条直线被哪条直线所截的角?它们是什么关系的角?∠A与∠5呢?∠A与∠6呢?
解：∠A与∠8是直线AB，DE被直线AC所截形成的内错角.∠A与∠5是直线AB，DE被直线AC所截形成的同旁内角.∠A与∠6是直线AB，DE被直线AC所截形成的同位角.
如图所示，指出图中各对角的位置关系：(1)∠C和∠D是 角；(2)∠B和∠GEF是 角；(3)∠A和∠D是 角， ∠B和∠C也是 角；(4)∠AGE和∠BGE是 角；(5)∠CFD和∠AFB是 角.
生活中的数学：三线八角手势记忆法
1.这节课研究的是两条直线被第三条直线所截形成的不同顶点处的两个角之间的位置关系，即同位角、内错角、同旁内角.
2.同位角、内错角、同旁内角的特点：