广东省惠州市2024-2025学年八年级上学期期末质量监测 数学模拟考试卷（含解析）

这是一份广东省惠州市2024-2025学年八年级上学期期末质量监测 数学模拟考试卷（含解析），共16页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
1．美术老师布置同学们设计窗花，下列作品为轴对称图形的是（ ）
A．B．
C．D．
2．三角形两边长分别为4，7，则第三边长不可能是（ ）
A．3B．5C．7D．9
3．华夏飞天续锦章，摘星揽月入天阊．2023年10月26日神舟十七号载人飞船在酒泉卫星发射中心圆满发射成功．此次神舟十七号载人飞船航天员空间站还将进行一系列科学实验，包括“空间蛋白质分子组装与应用研究”．其中某一蛋白质分子的直径仅米，这个数用科学记数法表示为（ ）
A．B．C．D．
4．经常开窗通风，可以有效地利用阳光和空气中的紫外线杀死病菌，清除室内空气中的有害气体，净化空气，如图，一扇窗户打开后，用窗钩AB可将其固定，这里所运用的几何原理是（ ）
A．三角形的稳定性B．两点之间线段最短
C．两点确定一条直线D．垂线段最短
5．下列各式从左到右的变形为分解因式的是（ ）
A．x（x﹣y）＝x2﹣xyB．x2+2xy+1＝x（x+2y）+1
C．（y﹣1）（y+1）＝y2﹣1D．x（x﹣3）+3（x﹣3）＝（x+3）（x﹣3）
6．下列计算正确的是（ ）．
A．B．
C．D．
7．如图，点为中边的中点，点为的中点，设，，下面结论正确的是（ ）
A．B．
C．D．、大小关系无法确定
8．“绿水青山就是金山银山”．某工程队承接了60万平方米的荒山绿化任务，为了迎接雨季的到来，实际工作时每天的工作效率比原计划提高了，结果提前30天完成了这一任务．设实际工作时每天绿化的面积x万平方米，则下面所列方程中正确的是（ ）
A．B．
C．D．
9．从边长为a的正方形中剪掉一个边长为b的正方形（如图1所示），然后将剩余部分拼成一个长方形（如图2所示），根据图形的变化过程，写出的一个正确的等式是（ ）
A．B．
C．D．
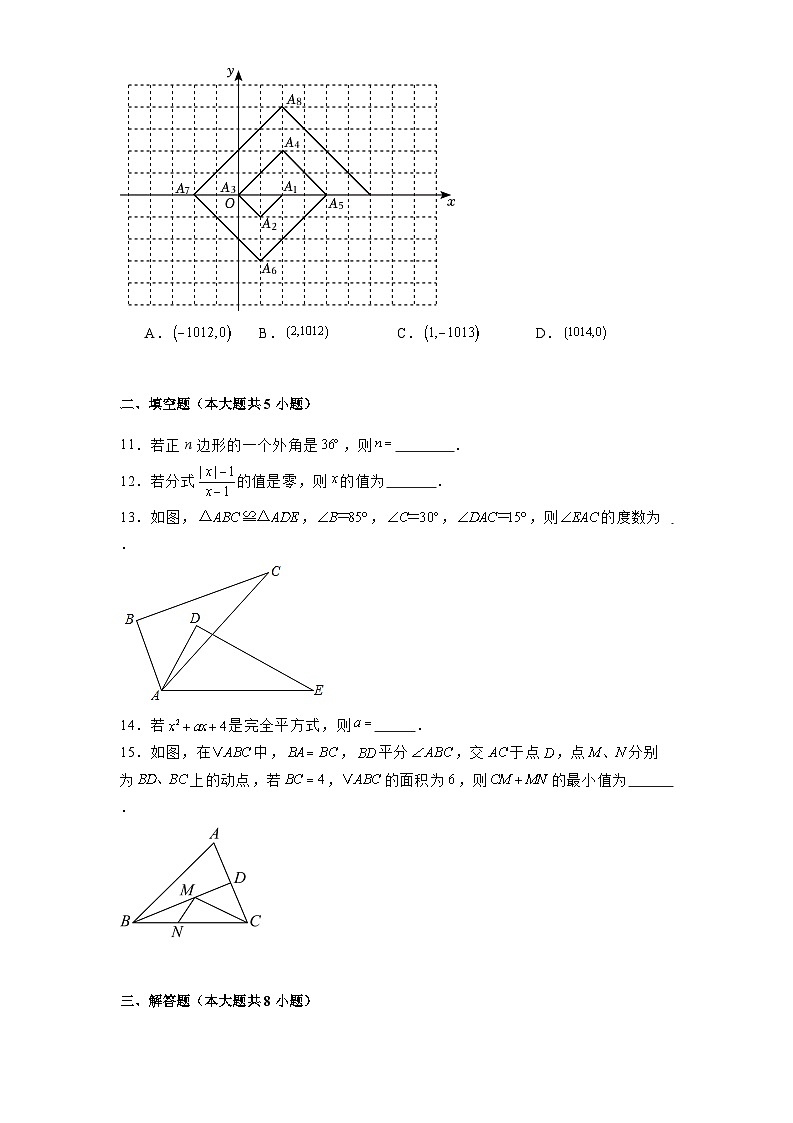
10．如图，在平面直角坐标系中，三角形，三角形，三角形，…，是斜边在轴上，斜边长分别为的等腰直角三角形．若三角形的顶点坐标分别为，则依图中所示规律，的坐标为（ ）
A．B．C．D．
二、填空题（本大题共5小题）
11．若正n边形的一个外角是，则 ．
12．若分式的值是零，则的值为 ．
13．如图，，，，，则的度数为 ．
14．若是完全平方式，则 ．
15．如图，在中，，平分，交于点，点分别为上的动点，若，的面积为，则的最小值为 ．
三、解答题（本大题共8小题）
16．如图，点B，E，C，F在一条直线上，．求证：．
17．解分式方程：．
18．先化简，再求值：，并从1，2，3这三个数中取一个合适的数作为的值代入求值．
19．如图，在中，，．
(1)尺规作图：作的中垂线，交于点M，交于点N．（不写作法，保留作图痕迹）
(2)在（1）所作的图形中，求证：．
20．如图，在平面直角坐标系中，，，．
(1)在图中画出关于轴对称的；
(2)在轴上作出一点，使最小，并直接写出点的坐标．（保留作图痕迹，不要求写作法）
(3)若点与点关于轴对称，求的值．
21．一辆汽车开往距离出发地km的目的地，出发后第一小时内按照原计划的速度匀速行驶，一小时后以原来速度的1.5倍匀速行驶．设原计划的行驶速度为x km/h．
(1)原计划到达目的地所用的时间为______h，实际用时为______h；
(2)若实际比原计划提前20min到达，求这辆汽车原计划到达目的地所用的时间，
22．问题情境阅读：若满足，求的值，解：设，，则，，所以．请仿照上例解决下面的问题：
问题发现：（1）若满足，求的值；
类比探究：（2）若满足，求的值；
拓展延伸：（3）如图，正方形的边长为，，，长方形的面积为，四边形和都是正方形，四边形是长方形，直接写出四边形的面积．（结果必须是一个具体数值）

23．如图，已知点，，其中、满足，且分式的值为0，将线段绕点顺时针旋转至，连接、．
(1)直接写出点、的坐标；
(2)求的度数；
(3)若，的平分线交于点，探究线段、、之间的数量关系，并证明你的结论．
参考答案
1．【答案】A
【分析】根据如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可．
【详解】解：A、是轴对称图形，故此选项符合题意；
B、不是轴对称图形，故此选项不合题意；
C、不是轴对称图形，故此选项不合题意；
D、不是轴对称图形，故此选项不合题意；
故此题答案为A．
2．【答案】A
【分析】根据三角形的三边关系：任意两边之和大于第三边，两边之差小于第三边，即可得答案．
【详解】解：根据三角形的三边关系：7﹣4＜x＜7+4，
解得：3＜x＜11，
故第三边长不可能是：3，
故此题答案为A．
3．【答案】C
【分析】科学记数法的表示形式为的形式，其中，为整数．确定的值时，要看把原数变成时，小数点移动了多少位，的绝对值与小数点移动的位数相同．当原数绝对值时，是正整数；当原数的绝对值时，是负整数
【详解】解：．
故此题答案为C．
4．【答案】A
【分析】由三角形的稳定性即可得出答案．
【详解】解：一扇窗户打开后，用窗钩可将其固定，这里所运用的几何原理是三角形的稳定性，
故此题答案为A．
5．【答案】D
【分析】根据因式分解的定义：将多项式和的形式化为整式积的形式，判断即可.
【详解】解：A、没把一个多项式转化成几个整式积，故A错误；B、没把一个多项式转化成几个整式积，故B错误；C、是整式的乘法，故C错误；D、把一个多项式转化成几个整式积，故D正确；
故此题答案为D.
6．【答案】B
【分析】根据分式的除法，分式的乘方，负整数指数幂及分式加法法则分别计算，从而作出判断．
【详解】解：A选项：，故A错误；
B选项：，故B正确；
C选项：，故C错误；
D选项：，故D错误．
故此题答案为B．
7．【答案】C
【分析】根据中线把三角形的面积分成相等的部分，可得到答案．
【详解】解：点为中边的中点
点为的中点
，
，
故此题答案为C．
8．【答案】C
【分析】设实际工作时每天绿化的面积x万平方米，根据工作时间工作总量工作效率，结合提前 30 天完成任务，即可得出关于x的分式方程．
【详解】解：设实际工作时每天绿化的面积x万平方米，则原计划每天绿化的面积万平方米，
依题意得： 即．
故此题答案为C．
9．【答案】D
【分析】用代数式分别表示图1中阴影部分以及图2的面积即可．
【详解】解：图1中阴影部分可以看作两个正方形的面积差，即，
图2是长为，宽为的长方形，因此面积为，
所以有，
故此题答案为D．
10．【答案】D
【分析】由图形中点的位置得到落在轴上的点都是奇数点，则这点在轴上，；类推每4个为一组，得到在点的右侧，由图形观察得到点的横坐标间相差2，故可得到的横坐标，得到结果．
【详解】∵根据图中点坐标特点，奇数点均在轴上，
∴在轴上，且纵坐标为0，
∵，，以此类推，每4个为一组，且，
∴在点的右侧，其横坐标为正数，
∵，
∴的横坐标为，
∴，
∴的坐标为，
故此题答案为D．
11．【答案】10
【分析】利用多边形的外角和即可解决问题．
【详解】解：因为正多边形的每一个外角都相等，
所以．
12．【答案】
【分析】根据分式的值为及有意义的条件判断即可．
【详解】解：由题得且，
解得：
13．【答案】
【分析】根据三角形内角和定理求出，根据全等三角形的性质得出，再求出答案即可．
【详解】解：∵，，
∴，
∵，
∴，
∵，
∴
14．【答案】
【分析】根据完全平方公式，得，展开计算即可．
【详解】解：根据题意，得，
解得．
15．【答案】3
【分析】根据等腰三角形的性质可知，BD垂直平分，根据垂直平分线的性质得出，由此可得，又由“两点之间线段最短”和“垂线段最短”可得当三点共线且时最短，根据三角形的面积公式可求出的长，即的最小值
【详解】解：如图，连接，
∵在中，，平分，
∴，，
∴垂直平分，
∴，
∴，
如图，当三点共线且时， ，此时最小，即的值最小，
∵，
∴，
解得，
∴的最小值为
16．【答案】见解析
【分析】由以及等式的性质得到，利用得到三角形与三角形全等，利用全等三角形对应角相等即可证明结论．
【详解】证明：∵，
∴，即，
∵在和中，
，
∴，
∴．
17．【答案】
【分析】先去分母变分式方程为整式方程，然后解整式方程，最后对方程的解进行检验即可．
【详解】解：，
去分母得：，
去括号得：，
移项，合并同类项得：，
系数化为1得：，
检验：把代入得：，
∴是原方程的解．
18．【答案】，取代入得
【分析】根据分式的化简求值，利用分式的通分化简，把除法化为乘法，然后约分化简，代入合适的值计算即可．
【详解】
在分式化简过程中，当x取1，3时分式分母为0，分式就无意义，
所以取
将代入得：
19．【答案】(1)图见解析
(2)证明见解析
【分析】（1）分别以点A和点C为圆心，以大于为半径画弧得到两个交点，过两交点作直线，标上点M和点N即可；
（2）连接，根据中垂线的性质证明，根据等角对等边得到，则，则，即可得到结论．
【详解】（1）解：如图所示，直线即为所求，
（2）证明：连接，
∵，．
∴，
∵的中垂线，交于点M，交于点N．
∴，
∴，
∴，
∴，
∴，
∴，
∴，
∴
20．【答案】(1)见解析
(2)
(3)1
【分析】此题考查作轴对称图形、最短路径问题、代数式求值，熟练掌握关于坐标轴对称的点的坐标特征是解答的关键．
（1）根据关于y轴对称的点的纵坐标相同，横坐标互为相反数得到对应点，再顺次连接即可画出对称图形；
（2）找到点A关于x轴的对称点，连接交x轴于点P，此时最小，由图知点P坐标；
（3）根据关于x轴对称的点的横坐标相同，纵坐标互为相反数得到关于a、b的方程，求得a、b值代入求解即可．
【详解】（1）解：如图，即为所求作：
（2）解：如图，作点A关于x轴的对称点，连接交x轴于点P，此时最小，
由图知，；
（3）解：∵点与点关于轴对称，
∴，，
∴，，
∴．
21．【答案】(1)，
(2)小时
【分析】（1）根据题意可分别得出原计划所用时间和实际所用时间；
（2）根据题意用原计划所用时间减去实际所用时间等于20分钟，注意单位换算即可得到本题答案．
【详解】（1）解：∵开往距离出发地km的目的地，原计划的行驶速度为x km/h，
∴原计划所用时间为：h，
∵一小时后以原来速度的1.5倍匀速行驶，
∴实际速度为：km/h，
∴根据题意实际用时为：h；
综上所述：原计划到达目的地所用的时间为h，实际用时为h；
（2）解：∵实际比原计划提前20min到达，即：，
∴可列方程：，解得：，
检验：把代入最简公分母中，，
故为方程的解且符合题意，
∴这辆车原计划到达目的地所用的时间：小时．
22．【答案】（1）；（2）；（3）
【分析】（1）根据例题的解题思路，进行计算即可解答；
（2）根据例题的解题思路，进行计算即可解答；
（3）根据题意可得：四边形是正方形，然后设，，则，，从而可得，，最后根据完全平方公式进行计算，即可解答．
【详解】解：（1）设，，
∴，
∵，
∴，
∴
，
∴的值为；
（2）设，，
∴，
∵，
∴，
∵，
∴，
∴，
∴，
∴的值为；
（3）四边形的面积为，
理由：由题意得：四边形是正方形，
设，，
∵正方形的边长为，，，
∴，
，
∴，
∵长方形的面积为，
∴，
∴正方形的面积：
，
∴四边形的面积为．
23．【答案】(1)
(2)
(3)
【分析】（1）根据分式的值为0及分别求出、，得到两点的坐标；
（2）由等腰三角形的性质及三角形内角和定理可求出答案；
（3）证出，在上截取，连接，证明，得出，证明是等边三角形，得出，则可得出结论．
【详解】（1）分式的值为0，
又
（2）
设
，
，
（3）
理由如下：在上截取，连接
平分
由（1）可知，
又
是等边三角形，