广东省深圳市光明区2024-2025学年八年级上学期期末 数学模拟试卷（含解析）

这是一份广东省深圳市光明区2024-2025学年八年级上学期期末 数学模拟试卷（含解析），共18页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
1．9的算术平方根是（ ）
A．﹣3B．±3C．3D．
2．已知是方程的一个解，那么常数的值是（ ）
A．5B．C．3D．
3．在中，的对边分别记为a，b，c，则由下列条件能判定为直角三角形的有（ ）
（1）
（2）
（3）
（4）
A．1个B．2个C．3个D．4个
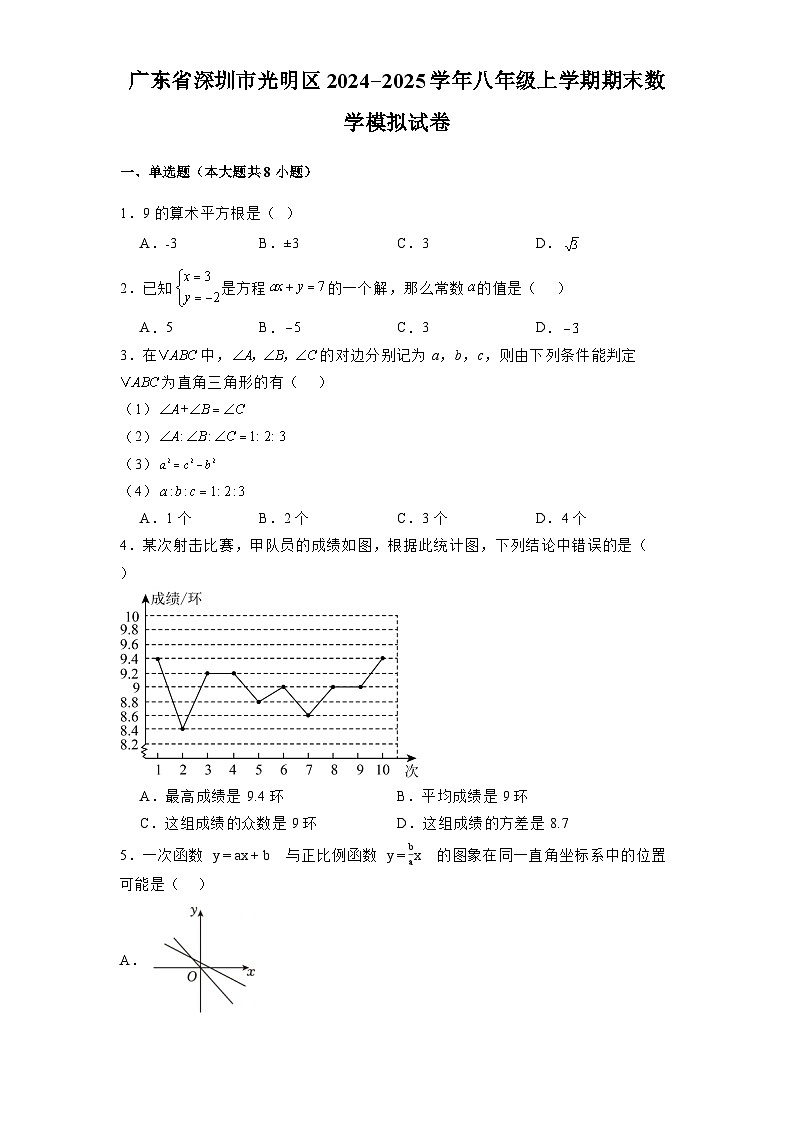
4．某次射击比赛，甲队员的成绩如图，根据此统计图，下列结论中错误的是（ ）

A．最高成绩是9.4环B．平均成绩是9环
C．这组成绩的众数是9环D．这组成绩的方差是8.7
5．一次函数 y=ax+b 与正比例函数 y=bax 的图象在同一直角坐标系中的位置可能是（ ）
A．
B．
C．
D．
6．甲、乙两队举行了“庆祝改革开放45周年”的赛龙舟比赛，两队在比赛时的路程（米）与时间（分钟）之间的函数关系如图所示，请你根据图象判断，下列说法正确的是（ ）

A．甲队率先到达终点
B．甲队比乙队多走了200米
C．乙队比甲队少用0.2分钟
D．比赛中两队从出发到2.2分钟时间段，乙队的速度比甲队的速度大
7．如图，ABCD，∠ABE＝∠EBF，∠DCE＝∠ECF，设∠ABE＝α，∠E＝β，∠F＝γ，则α，β，γ的数量关系是（ ）
A．4β﹣α+γ＝360°B．3β﹣α+γ＝360°
C．4β﹣α﹣γ＝360°D．3β﹣2α﹣γ＝360°
8．一次函数与一次函数在同一坐标系中的图象如图所示，两条直线交于点，与两坐标轴分别交于四个点．则下列结论：
①一元一次方程的解为；②；③方程组的解为；④四边形的面积为，正确的是（ ）
A．B．C．D．
二、填空题（本大题共5小题）
9．若点与点关于y轴对称，则 ．
10．某校为推荐一项作品参加“科技创新”比赛，对甲、乙、丙、丁四项候选作品进行量化评分，具体成绩（百分制）如下表：如果按创新性占，实用性占计算总成绩，那么甲、乙、丙、丁中应推荐的作品是 ．
11．如图，中，，将三角形沿AD折叠，使点C落在上的点E处，则的长为 ．
12．如图，和的角平分线交于点E，延长交CD于点F，，则 ．
13．如图，所有正方形的中心都在原点，且各边也都与轴或轴平行，从内向外，它们的边长依次为，，，，，顶点依次用、、、表示，则顶点的坐标为 ．

三、解答题（本大题共7小题）
14．计算：
(1)；
(2)．
15．解方程组；
(1)
(2)
16．在平面直角坐标系中的位置如图所示，A、B、C三点在格点上．
(1)作出关于x轴对称的，并写出点的坐标；
(2)在轴上求作点，使得最小，请你直接写出点坐标；
(3)若点为x轴上一动点，且满足的面积为1，请你直接写出点坐标．
17．为了解八年级学生的体质健康状况，某校对八年级(10)班43名同学进行了体质检测（满分10分，最低5分），并按照男女把成绩整理如图：
八年级（10）班体质检测成绩分析表
（1）求八年级（10）班的女生人数．
（2）根据统计图可知，a＝ ，b＝ ，c＝ ．
（3）若该校八年级一共有860人，则得分在8分及8分以上的人数共有多少人？
18．我市某中学计划举行以“奋斗百年路，启航新征程”为主题的知识竞赛，并对获奖的同学给予奖励．现要购买甲、乙两种奖品，已知1件甲种奖品和2件乙种奖品共需40元，2件甲种奖品和3件乙种奖品共需70元．
（1）求甲、乙两种奖品的单价；
（2）根据颁奖计划，该中学需甲、乙两种奖品共60件，且甲种奖品的数量不少于乙种奖品数量的，应如何购买才能使总费用最少？并求出最少费用．
19． 中，，点D，E分别是边上的点，点P是一动点，令，，．
(1)如图1，若点P在线段上，且，则 ；
(2)如图2，若点P在线段上运动，则之间的关系为 ；
(3)如图3，若点P在线段的延长线上运动，则之间的关系为 ．
(4)如图4，若点P运动到的内部，写出此时之间的关系，并说明理由．
(5)若点P运动到的外部，且与点A分别位于直线两侧时，请在图5中画出一种情形，直接写出此时之间的关系，无需说明理由．
20．如图，直线与x轴y轴分别相交于点E，F．点E的坐标，点A的坐标为．点是直线上的一个动点（点P不与点E，F重合）．
(1)求k的值；
(2)在点P运动的过程中，求出的面积S与x的函数关系式．
(3)若的面积为，求此时点P的坐标．
参考答案
1．【答案】C
【详解】9的算术平方根是3，
故此题答案为C．
2．【答案】C
【分析】将代入方程可得关于的一元一次方程，解方程即可得出答案．
【详解】解：由题意得：，
解得：，
故此题答案为C．
3．【答案】C
【分析】根据三角形内角和定理和勾股定理逐项判断即可得出答案．
【详解】解：（1）∵，，
∴，
∴，
∴为直角三角形；
（2）∵，，
∴，
∴为直角三角形；
（3）∵，
∴，
∴为直角三角形；
（4）∵，
∴设，，（其中），
∴，
∴不是直角三角形，
故此题答案为C．
4．【答案】D
【分析】根据统计图即可判断选项A，根据统计图可求出平均成绩，即可判断选项B，根据统计图即可判断选项C，根据所给数据进行计算即可判断选项D．
【详解】解：A、由统计图得，最高成绩是9.4环，选项说法正确，不符合题意；
B、平均成绩：，选项说法正确，符合题意；
C、由统计图得，9出现了3次，出现的次数最多，选项说法正确，不符合题意；
D、方差：，选项说法错误，符合题意；
故此题答案为D．
5．【答案】A
【详解】解：A、由一次函数的图象可得 a0 ，则 ba0 ，则 ba>0 ，而正比例函数图象可得 ba0，
∴w随m的增大而增大，
∴当m=20时，w有最小值，最小值为10×20+600=800（元），
∴购买甲种奖品20件，乙种奖品40件时总费用最少，最少费用为800元．
19．【答案】(1)130
(2)
(3)
(4)，理由见解析
(5)或
【分析】（1）连接，证明即可得到答案；
（2）同（1），证明即可得到答案；
（3）利用三角形外角的性质求解即可；
（4）利用三角形外角的性质求解即可；
（5）根据题意画出图形，利用三角形外角的性质求解即可．
【详解】（1）解：如图，连接，
∵，，
∴，
∵，，
∴
（2）解：如图，连接，
∵，，
∴
（3）解：设与交于F，
∵，，
∴，
∴
（4）解：，理由如下：
如图所示，连接，
∵，，
∴，
∴；
（5）解：或．
如图，

∵，，，
∴ ；
如图，
∵，，，
∴，
综上可知，或．
20．【答案】(1)
(2)
(3)P的坐标为(，)或(，)
【分析】（1）直接把点E的坐标代入直线求出k的值即可；
（2）过点P作于点D，用x表示出的长（注意分情况讨论），根据三角形的面积公式即可得出结论；
（3）把的面积为代入（2）中关系式，求出x的值，把x的值代入直线一次函数解析式中即可得出结论．
【详解】（1）解：把点E的坐标代入直线得，
解得.
∴；
（2）过点P作于点D，
∵点是直线上的一个动点，
∴当时，，当时，
∵点A的坐标为，
∴当时，，
当时，，
综上可得：；
（3）∵的面积为，
∴当时，，
解得；
将代入，得，
∴P(，)；
当时，，
解得；
将代入，得，
∴P(，)；
综上可得：点P的坐标为(，)或(，)．项目作品
甲
乙
丙
丁
创新性
实用性
平均数
中位数
众数
方差
男生
7.48
8
c
1.99
女生
a
b
7
1.74