人教版（2024）八年级下册18.1.2 平行四边形的判定课时练习

这是一份人教版（2024）八年级下册18.1.2 平行四边形的判定课时练习，共9页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
1．如图所示，直线a∥b，另有一条直线l与直线a，b分别交于点A，B，若将直线l作平移运动，则线段AB的长度（ ）
A．变大
B．变小
C．不变
D．变大或变小要看直线l平移的方向
2．如图，在平行四边形ABCD中，对角线AC、BD相交于点O，E是边BC的中点，AB=4，则OE=（ ）.
A．1B．2C．4D．8
3．如图， ▱ABCD的顶点A，D分别在直角∠MON的两边OM，ON上运 动（不与点O重合），▱ABCD的对角线AC，BD相交于点P，连接OP，若OP=5，则▱ABCD的周长最小值是（ ）
A．20B．25C．10D．15
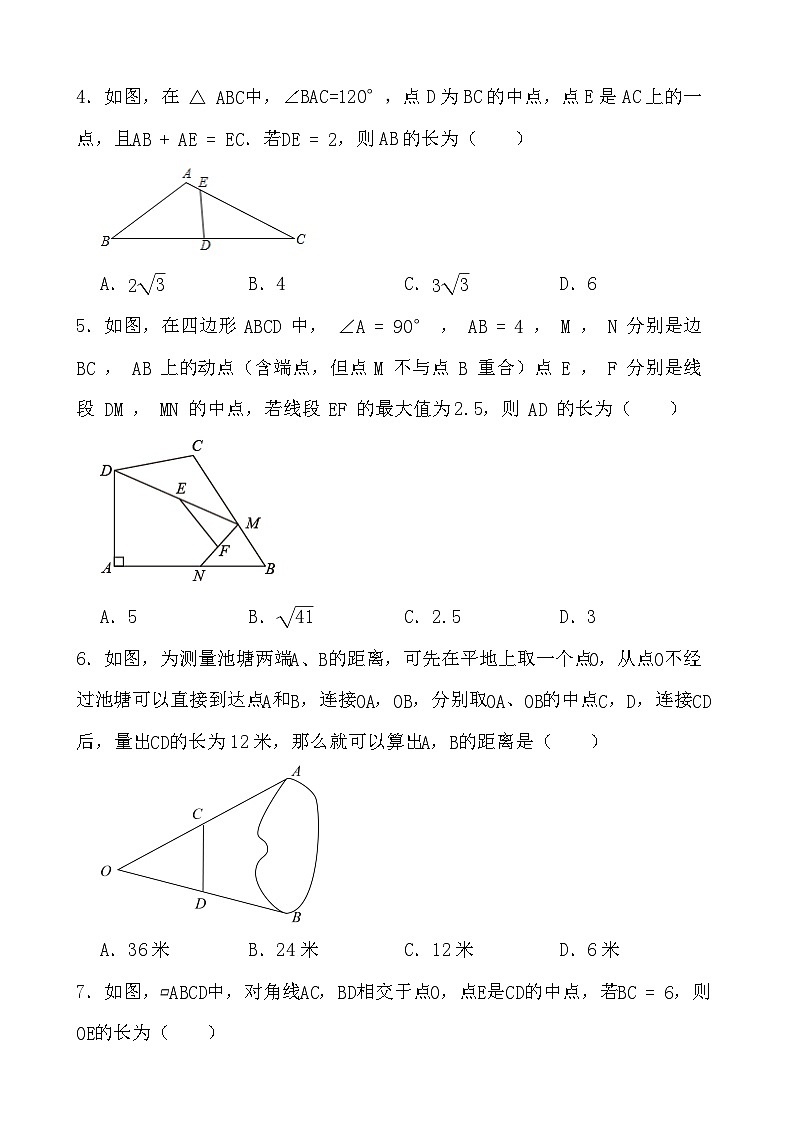
4．如图，在△ABC中，∠BAC=120°，点D为BC的中点，点E是AC上的一点，且AB+AE=EC．若DE=2，则AB的长为（ ）
A．23B．4C．33D．6
5．如图，在四边形 ABCD 中， ∠A=90° ， AB=4 ， M ， N 分别是边 BC ， AB 上的动点（含端点，但点 M 不与点 B 重合）点 E ， F 分别是线段 DM ， MN 的中点，若线段 EF 的最大值为2.5，则 AD 的长为（ ）
A．5B．41C．2.5D．3
6．如图，为测量池塘两端A、B的距离，可先在平地上取一个点O，从点O不经过池塘可以直接到达点A和B，连接OA，OB，分别取OA、OB的中点C，D，连接CD后，量出CD的长为12米，那么就可以算出A，B的距离是（ ）
A．36米B．24米C．12米D．6米
7．如图，▱ABCD中，对角线AC，BD相交于点O，点E是CD的中点，若BC=6，则OE的长为（ ）
A．3B．12C．8D．10
8．如图，四边形ABCD的对角线AC，BD相交于点O，下列条件不能判定四边形ABCD是平行四边行的是（ ）
A．OA＝OC，OB＝ODB．AB＝CD，AD＝BC
C．AB∥CD，AD＝BCD．∠ABD＝∠CDB，∠ADB＝∠CBD
二、填空题
9．如图，已知△ABC中，AB=AC，AD平分∠BAC，点E是AB的中点，若AC=6，则DE的长为 .
10．如图，在 △ABC 中， ∠ACB=90° ， M ， N 分别是 AB ， AC 的中点，延长 BC 至点 D ，使 CD=13BD ，连接 DM ， DN ， MN ．若 AB=6 ，则 DN 的长为 ．
11．如图，在四边形ABCD中，∠A＝∠B＝90°，AD∥BC，且AD＞BC，AB＝BC＝10，点P在BC边上，点B关于直线AP的对称点为Q，CQ的延长线交边AD于点R，如果AR＝CP，那么线段AP的长为 ．
12．如图，在四边形 ABCD 中， CD 平分对角线 AC 与 BC 边延长线的夹角， AD⊥DC ，点 E 为 AB 中点，若 AC=4 ， BC=6 ，则线段 DE 的长为 .
13．如图，在△ABC中，AB=4，AC=5，BC=6，点D，E，F分别是AB，BC，CA的中点，连结DE，EF，则四边形ADEF的周长为 ．
三、解答题
14．如图，在▱ABCD中，点E、F分别在AD、BC上，且AE＝CF．求证：四边形BFDE是平行四边形．
15．如图，已知 ▱ ABCD中，E、F分别是AD、BC边上的点，DE＝BF，求证：AF // CE.
16．如图，在△ABC中，AB=AC，AD是BC边上的中线，四边形ADBE是平行四边形，求证：四边形ADBE是矩形.
17．如图，已知AB=DC，DE⊥AC，BF⊥AC，垂足分别为 E ， F ，且DE=BF.
求证：四边形 ABCD 是平行四边形.
18．如图，在平行四边形ABCD中，点E、F分别在AD、BC上，且AE＝CF.求证：BE//DF.
参考答案：
1．C
2．B
3．A
4．B
5．D
6．B
7．A
8．C
9．3
10．3
11．55
12．5
13．9
14．证明：∵四边形ABCD是平行四边形，
∴AD∥BC，AD＝BC，
∵AE＝CF，
∴AD﹣AE＝BC﹣CF，
∴ED＝BF，
又∵AD∥BC，
∴四边形BFDE是平行四边形．
15．证明：∵四边形ABCD是平行四边形
∴AD=BC ， AD ∥ BC
∵DE=BF
∴AD-DE=BC-BF
∴AE=CF
而AE ∥ CF
∴四边形AECF是平行四边形
∴AF ∥ CE
16．证明：∵AB=AC，AD 是BC边上的中线，
∴AD⊥BC ，
∴∠ADB=90° .
又∵四边形ADBE是平行四边形，
∴四边形ADBE是矩形.
17．证明：∵DE⊥AC，BF⊥AC，
∴∠DEC=∠BFC=90°，
在Rt△DEC和Rt△BFA中，
AB=DCBF=DE ，
∴Rt△DEC≌Rt△BFA（HL），
∴∠DCE=∠BAF，
∴AB∥DC，
又∵AB=DC，
∴四边形ABCD是平行四边形.
18．证明：∵四边形ABCD是平行四边形
∴AD＝BC，AD//BC，
∵AE＝CF，
∴DE＝BF，
又∵DE//BF，
∴四边形BEDF是平行四边形，
∴BE//DF.