七年级下册（2024）7.2.3 平行线的性质背景图ppt课件

这是一份七年级下册（2024）7.2.3 平行线的性质背景图ppt课件，共24页。PPT课件主要包含了学习目标，新课导入，两直线平行，进行新课，活动1，活动2，符号语言，直线a∥b，∠3∠160°，∠2+∠3180°等内容，欢迎下载使用。
1.理解平行线的性质.2.能运用平行线的性质进行推理.
问题：平行线的判定方法有哪些？
1.同位角相等2.内错角相等3.同旁内角互补
1.同位角？2.内错角？3.同旁内角？
思考：反过来，如果两条直线平行，同位角、内错角、同旁内角各有什么关系？
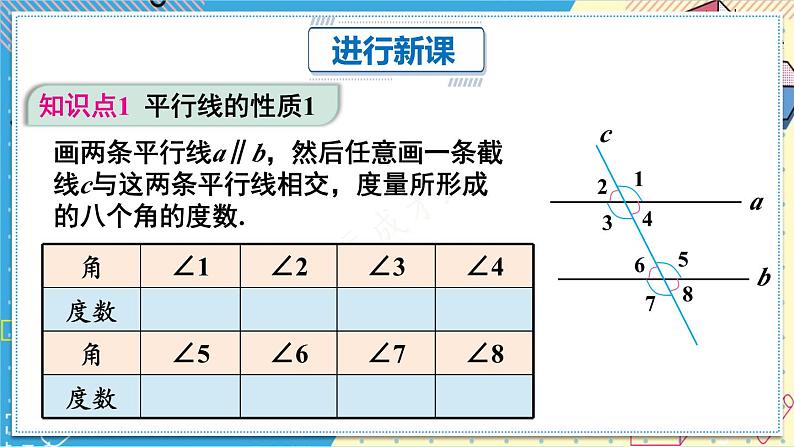
画两条平行线a∥b，然后任意画一条截线c与这两条平行线相交，度量所形成的八个角的度数.
观察：在∠1，∠2，…，∠8中，哪些是同位角？它们的度数有什么关系？
同位角：∠1和∠5，∠2和∠6，∠3和∠7，∠4和∠8.
猜想：两条平行线被第三条直线所截得的同位角_____.
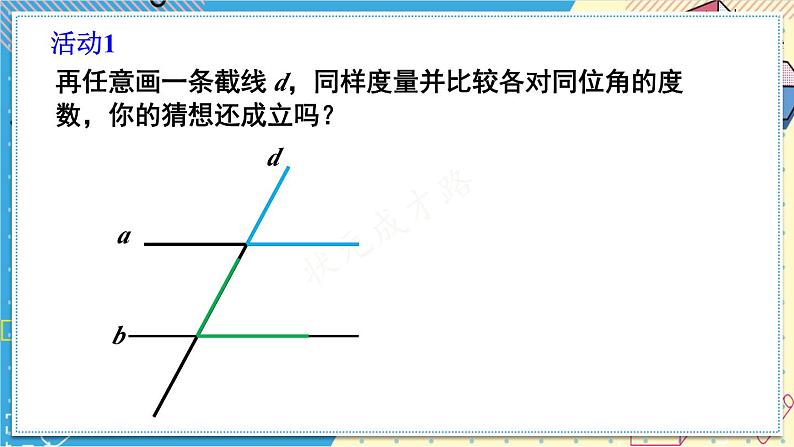
再任意画一条截线 d，同样度量并比较各对同位角的度数，你的猜想还成立吗？
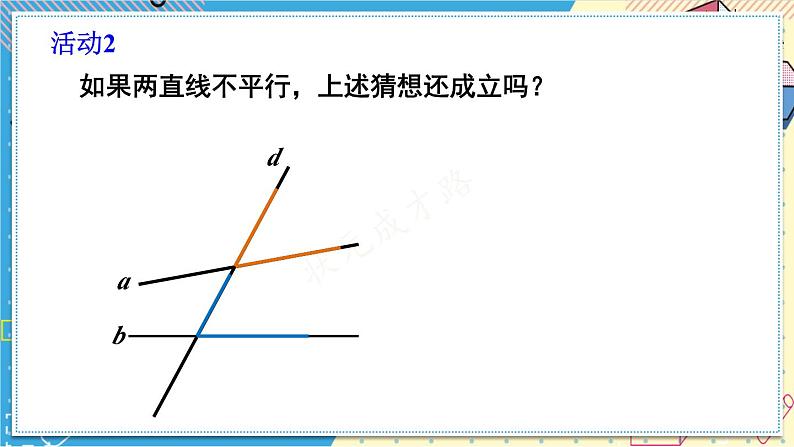
如果两直线不平行，上述猜想还成立吗？
性质1 两条平行直线被第三条直线所截，同位角相等.简单说成：两直线平行，同位角相等.
∵a∥b（已知），∴ ∠1=∠2（两直线平行，同位角相等）.
练习1 如图，直线a∥b，直线c与a，b相交.若∠1=60°，则∠2的度数为______.
前面我们利用“同位角相等，两直线平行”推出了“内错角相等，两直线平行”.类似地，你能由性质1推出两条平行线被第三条直线截得的内错角之间的关系吗？
如图，已知 a∥b，那么2 与3 相等吗？为什么？
解：∵ a∥b，(已知)∴∠1=∠2.(两直线平行，同位角相等)又∵ ∠1=∠3，(对顶角相等)∴ ∠2=∠3.(等量代换)
性质2 两条平行直线被第三条直线所截，内错角相等.简单说成：两直线平行，内错角相等.
∵a∥b（已知），∴ ∠1=∠2（两直线平行，内错角相等）.
练习2 如图，平行线AB，CD被直线EF所截，FG平分∠EFD.若∠EFD=70°，则∠EGF的度数是_____.
类似地，已知两直线平行，能否得到同旁内角之间的数量关系？
如图，已知 a∥b，那么2 与4 有什么关系呢？为什么？
解: ∵a//b ，(已知)∴ 1=  2.(两直线平行，同位角相等)∵  1+  4=180°，(邻补角的性质)∴ 2+  4=180°.(等量代换)
性质3 两条平行直线被第三条直线所截，同旁内角互补.简单说成：两直线平行，同旁内角互补.
∵a∥b（已知），∴ ∠1+∠2=180°（两直线平行，同旁内角互补）.
练习3 如图，直线l1∥l2，l3∥l4.若∠1=70°，则∠2的度数是_____.
解：因为梯形上、下两底DC与AB互相平行，根据“两直线平行，同旁内角互补”，可得∠A与∠D互补，∠B和∠C互补，于是
∠D=180°－∠A=180°－100°=80°，
∠C=180°－∠B=180°－115°=65°.
所以梯形的另外两个角∠D，∠C分别是80°，65°.
例1 如图是一块梯形铁片的残余部分，量得∠A=100°，∠B=115°，梯形的另外两个角∠D，∠C分别是多少度？
平行线的判定和性质的联系和区别
同位角相等内错角相等同旁内角互补
1.如图，直线a // b，∠1=54°，∠2，∠3，∠4各是多少度？
【选自教材P17“练习”】
解：∵a∥b，∠1=54°，∴∠4 =∠1 = 54°（两直线平行，同位角相等）.∠3 =180°－∠4=180° － 54°=126°，∵∠2 与∠1 是对顶角，∴∠2=∠1= 54°.
2.如图，在三角形ABC中，D是AB上一点，E是AC上一点，∠ADE=60°，∠B=60°，∠AED=40°.（1）DE和BC 平行吗？为什么？（2）∠C是多少度？为什么？
解：（1）DE 和 BC平行.理由：∵∠ADE=∠B.∴DE∥BC(同位角相等，两直线平行).（2）∵DE∥BC，∴∠C=∠AED=40°(两直线平行，同位角相等).
3. 将一个直角三角尺与两边平行的纸条如图装置，则下列结论正确的是___________（填序号）.①∠1=∠2； ②∠4+∠5=180°；③∠1+∠4=90°； ④∠4+90°=∠3.