










所属成套资源:人教版数学七年级下册(2024)课件+导学案+教学设计+分层作业(含答案)
初中数学人教版(2024)七年级下册(2024)7.2.3 平行线的性质精品教学作业ppt课件
展开
这是一份初中数学人教版(2024)七年级下册(2024)7.2.3 平行线的性质精品教学作业ppt课件,文件包含7231平行线的性质pptx、7231平行线的性质教学设计docx、7231平行线的性质分层作业原卷版docx、7231平行线的性质分层作业解析版docx、7231平行线的性质导学案docx等5份课件配套教学资源,其中PPT共32页, 欢迎下载使用。
1.掌握平行线的性质定理1:两条平行直线被第三条直线所截, 同位角相等;探索并证明平行线的性质定理2、3:两条平行直线被第三条直线所截,内错角相等(或同旁内角互补).2.经历平行线性质的探究过程,从中体会度量、猜想、验证、证明的几何研究方法,感受转化的数学思想.3.能够根据平行线的性质定理进行简单的推理,感受数学语言的简洁美,并能将学到的知识应用到生活中去,提高应用意识.
判定方法1 同位角相等, 两直线平行.判定方法2 内错角相等, 两直线平行.判定方法3 同旁内角互补, 两直线平行.
问题1 有哪些判定方法可以证明两条直线平行?
反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?
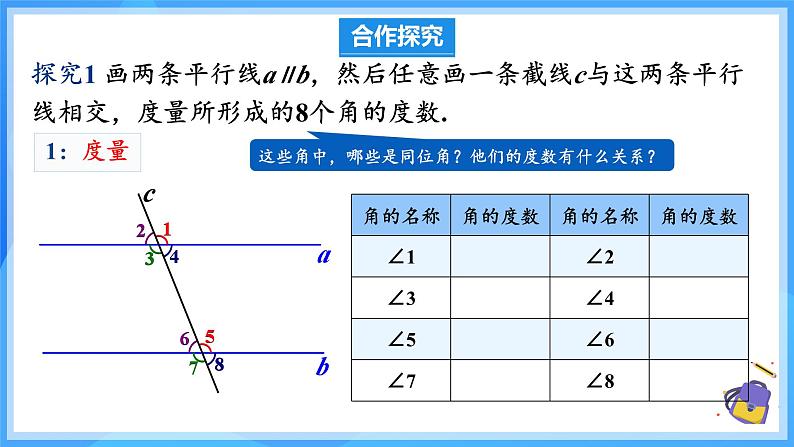
探究1 画两条平行线a∥b,然后任意画一条截线c与这两条平行线相交,度量所形成的8个角的度数.
这些角中,哪些是同位角?他们的度数有什么关系?
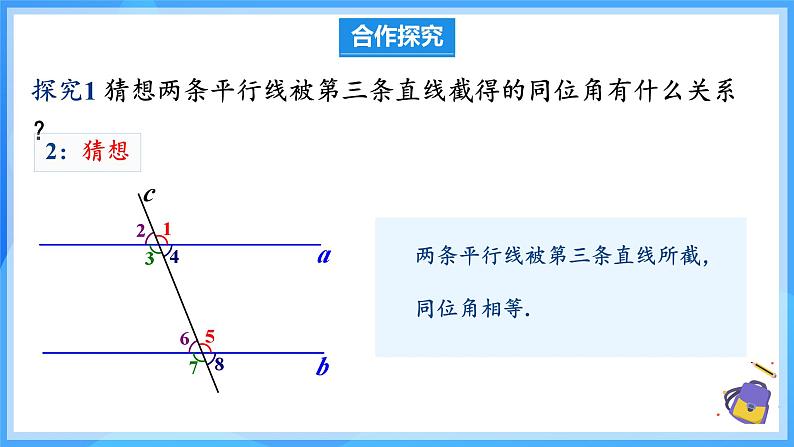
探究1 猜想两条平行线被第三条直线截得的同位角有什么关系?
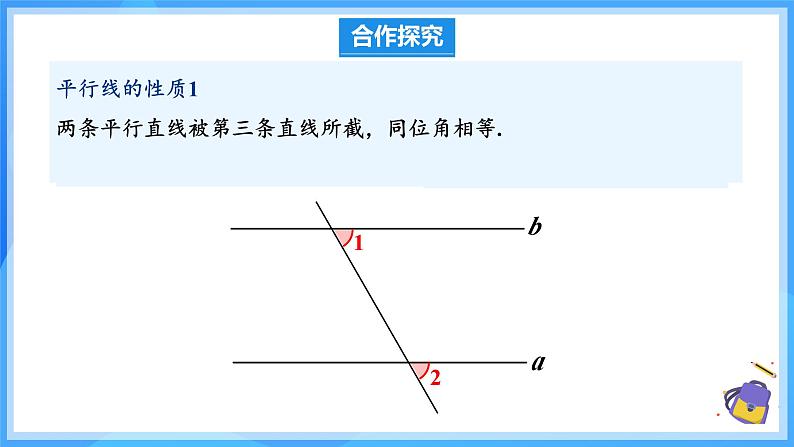
两条平行线被第三条直线所截, 同位角相等.
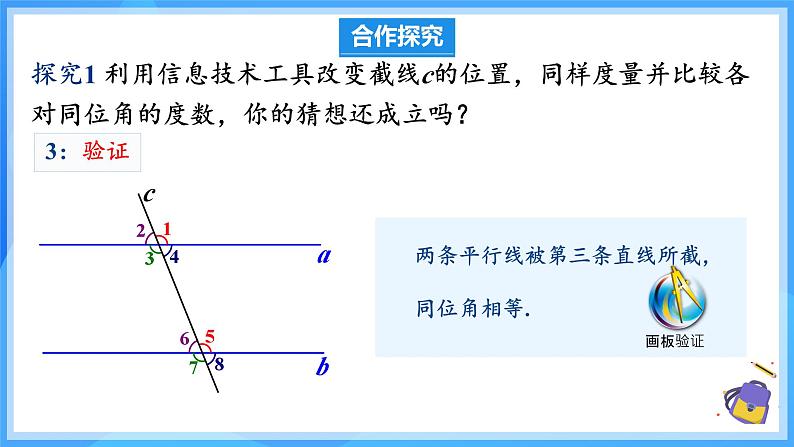
探究1 利用信息技术工具改变截线c的位置,同样度量并比较各对同位角的度数,你的猜想还成立吗?
平行线的性质1 两条平行直线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.(因为 a∥b,所以 ∠1=∠2.)
探究2 我们利用“同位角相等,两直线平行”推出了“内错角相等,两直线平行”,类似的,你能由性质1推出两条平行线被第三条直线截得的内错角之间的关系吗?
转化1:自然语言→符号语言
如图,平行线a,b被直线c所截,∠1和∠3的度数有什么关系?
转化2:内错角→同位角→平行线
证明:∵a∥b(已知),∴∠1=∠2(两直线平行,同位角相等),又 ∠3=∠2(对顶角相等),∴∠1=∠3(等量代换).
平行线的性质2 两条平行直线被第三条直线所截,内错角相等.简单说成:两直线平行,内错角相等.(因为 a∥b,所以 ∠1=∠2.)
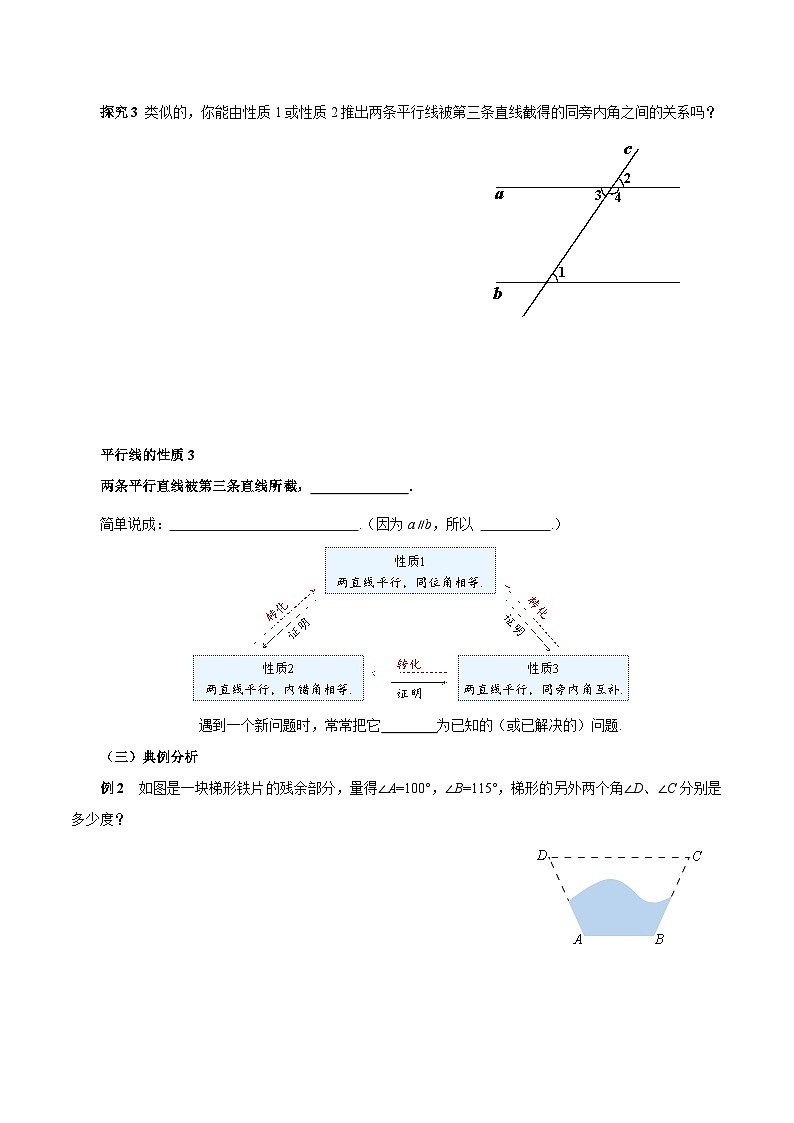
探究3 类似的,你能由性质1或性质2推出两条平行线被第三条直线截得的同旁内角之间的关系吗?
如图,平行线a,b被直线c所截,∠1和∠4的度数有什么关系?
答:∠1+∠4=180°.
探究3 我们利用“同位角相等,两直线平行”推出了“同旁内角互补,两直线平行”,类似的,你能由性质1推出两条平行线被第三条直线截得的同旁内角之间的关系吗?
转化2:同旁内角→同位角→平行线
证明:∵a∥b(已知),∴∠1=∠2(两直线平行,同位角相等),又 ∠2+∠4=180°(邻补角互补),∴∠1+∠4=180°(等量代换).
你还有其它证明方法吗?
探究3 我们利用“内错角相等,两直线平行”推出了“同旁内角互补,两直线平行”,类似的,你能由性质2推出两条平行线被第三条直线截得的同旁内角之间的关系吗?
转化2:同旁内角→内错角→平行线
证明:∵a∥b(已知),∴∠1=∠3(两直线平行,内错角相等),又 ∠3+∠4=180°(邻补角互补),∴∠1+∠4=180°(等量代换).
平行线的性质3 两条平行直线被第三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.(因为 a∥b,所以 ∠1+∠2=180°.)
遇到一个新问题时,常常把它转化为已知的(或已解决的)问题.
性质1 两直线平行,同位角相等.
性质2 两直线平行,内错角相等.
性质3 两直线平行,同旁内角互补.
例2 如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角∠D、∠C分别是多少度?
解:因为梯形上、下两底DC与AB互相平行,根据“两直线平行,同旁内角互补”,可得∠A与∠D互补,∠B与∠C互补,于是∠D=180°-∠A=180°-100°=80°,∠C=180°-∠B=180°-115°=65°.所以梯形的另外两个角∠D,∠C分别是80°,65°.
1. 如图,直线a∥b,∠1=54°,∠2、∠3、∠4各是多少度?
解:由题意得:∠2=∠1=54°(对顶角相等).∵a∥b(已知),∴∠3+∠2=180°(两直线平行,同旁内角互补),∠4=∠2(两直线平行,内错角相等),∴∠3=180°-∠2=180°-54°=126°,∠4=54°.
你还有其它计算方法吗?
2. 如图,在三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,∠AED=40°.(1)DE和BC平行吗?为什么?
解:(1)DE∥BC,理由如下:∵∠ADE=∠B=60°(已知).∴DE∥BC(同位角相等,两直线平行).
2. 如图,在三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,∠AED=40°.(2)∠C是多少度,为什么?
解:(2)∠C=40°,理由如下:∵DE∥BC(已证).∴∠C=∠AED=40°(两直线平行,同位角相等).
3. 如图,一条水渠两次转弯后,和原来的方向相同.如果第一次的拐角∠A是135°,第二次的拐角∠B是多少度?为什么?
解:∠B是135°,理由如下:∵水渠两次转弯后,和原来的方向相同,∴AC∥BD,∴∠B=∠A=135°(两直线平行,内错角相等).
4. 当光线从水中射向空气时,要发生折射,在水中平行的光线,折射到空气中也是平行的.如图,∠1=45°,∠2=122°,求图中∠3、∠4的度数.
解:根据“两直线平行,同位角相等”,可得:∠3=∠1=45°,∠4=∠2=122°.
5. 将一个直角三角尺与两边平行的纸条如图放置,则下列结论正确的是 (填序号).①∠1=∠2;②∠4+∠5=180°;③∠1+∠4=90°;④∠4+90°=∠3.
两直线平行,同位角相等.
两直线平行,同旁内角互补.
两直线平行,内错角相等.
6. 图中是对顶角量角器,你能说出用它测量角的原理吗?
解:根据“两直线平行,同位角相等”,可得:∠1=∠2,根据“对顶角相等”,可得:∠2=∠3,∴∠1=∠3.
1. (2024•重庆)如图,AB∥CD,∠1=65°,则∠2的度数是( ) A.105° B.115° C.125° D.135°
2. (2024•东营)已知,直线a∥b,把一块含有30°角的直角三角板如图放置,∠1=30°,三角板的斜边所在直线交b于点A,则∠2=( ) A.50° B.60° C.70° D.80°
3. (2024•淄博)如图,已知AD∥BC,BD平分∠ABC.若∠A=110°,则∠D的度数是( ) A.40° B.36° C.35° D.30°
4. (2024•福建)在同一平面内,将直尺、含30°角的三角尺和木工角尺(CD⊥DE)按如图方式摆放,若AB∥CD,则∠1的大小为( ) A.30° B.45° C.60° D.75°
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
两直线平行,同位角相等
两直线平行,内错角相等
两直线平行,同旁内角互补
探究性作业:如图,潜望镜中的两面镜子是互相平行放置的,光线经过镜子反射时,∠1=∠2,∠3=∠4,∠2和∠3有什么关系?为什么进入潜望镜的光线和离开潜望镜的光线是平行的?(提示:分析这两条光线被哪条直线所截.)
相关课件
这是一份七年级下册(2024)7.4 平移优秀教学作业ppt课件,文件包含7231平行线的性质pptx、7231平行线的性质教学设计docx、7231平行线的性质分层作业原卷版docx、7231平行线的性质分层作业解析版docx、7231平行线的性质导学案docx等5份课件配套教学资源,其中PPT共32页, 欢迎下载使用。
这是一份初中数学人教版(2024)八年级下册19.1.1 变量与函数优秀教学作业ppt课件,文件包含1913函数的图象含动画演示pptx、1913函数的图象教学设计docx、1913函数的图象分层作业原卷版docx、1913函数的图象分层作业解析版docx、1913函数的图象导学案docx等5份课件配套教学资源,其中PPT共39页, 欢迎下载使用。
这是一份初中数学19.1.1 变量与函数公开课教学作业ppt课件,文件包含1912函数含动画演示pptx、1912函数教学设计docx、1912函数分层作业原卷版docx、1912函数分层作业解析版docx、1912函数导学案docx等5份课件配套教学资源,其中PPT共28页, 欢迎下载使用。











