2024-2025学年湖南省长沙市高三上册11月月考数学检测试卷

这是一份2024-2025学年湖南省长沙市高三上册11月月考数学检测试卷，共5页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1. 若复数满足，则（ ）
A. B. C. D.
2. 已知数列的前项和，则等于（ ）
A. 12B. 15C. 18D. 21
3. 抛物线的焦点坐标为（ ）
A B.
C. D.
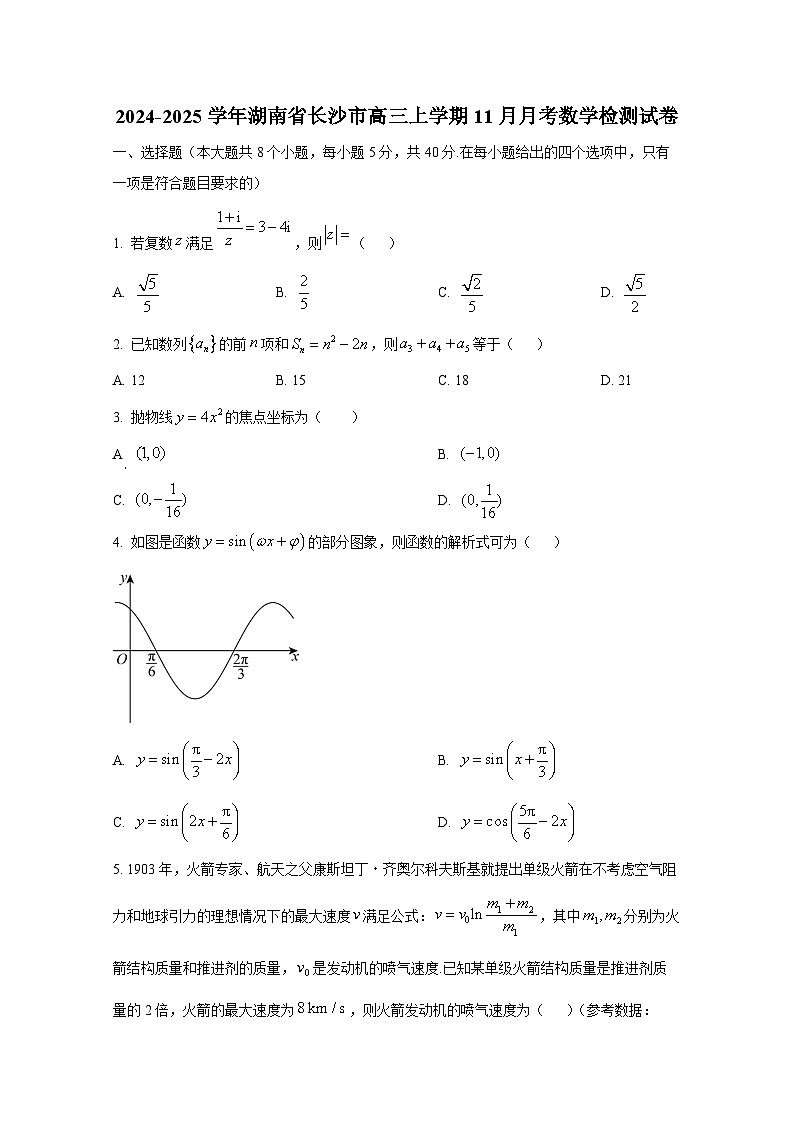
4. 如图是函数的部分图象，则函数的解析式可为（ ）
A. B.
C. D.
5. 1903年，火箭专家、航天之父康斯坦丁・齐奥尔科夫斯基就提出单级火箭在不考虑空气阻力和地球引力的理想情况下的最大速度满足公式：，其中分别为火箭结构质量和推进剂的质量，是发动机的喷气速度.已知某单级火箭结构质量是推进剂质量的2倍，火箭的最大速度为，则火箭发动机的喷气速度为（ ）（参考数据：，）
A. B. C. D.
6. 若，，则的值为（ ）
A. B. C. D.
7. 如图，一个质点从原点O出发，每隔一秒随机向左或向右移动一个单位长度，向左的概率为，向右的概率为，共移动4次，则该质点共两次到达1的位置的概率为（ ）

A. B. C. D.
8. 设为数列an的前n项和，若，且存在，，则的取值集合为（ ）
A. B.
C. D.
二、选择题（本大题共3小题，每小题6分，共18分.在每小题给出的选项中，至少有两项是符合题目要求，若全部选对得6分，部分选对得部分分，选错或不选得0分）
9. 如图，在正方体中，点，分别为，中点，则下列说法正确的是（ ）
A. 直线与为异面直线B. 直线与所成角为
C. D. 平面
10. 已知是圆上的动点，直线与交于点，则（ ）
A B. 直线与圆相切
C. 直线与圆截得弦长为D. 的值为
11. 已知三次函数有三个不同的零点，，，函数也有三个零点，，，则（ ）
A.
B. 若，，成等差数列，则
C.
D.
三、填空题（本大题共3个小题，每小题5分，共15分）
12. 已知随机变量服从二项分布，若，，则_____.
13. 已知平面向量，满足，，且在上的投影向量为，则为______.
14. 如图，已知四面体的体积为32，，分别为，的中点，，分别在，上，且，是靠近点的四等分点，则多面体的体积为_____.
四、解答题（本大题共5个小题，共77分.解答应写出文字说明、证明过程或演算步骤）
15. 设的内角，，的对边分别为，，，已知.
（1）求；
（2）若，且的面积为，求的值.
16. 设，.
（1）若，求在处的切线方程；
（2）若，试讨论的单调性.
17. 已知四棱锥，底面为菱形，为上的点，过的平面分别交于点，且∥平面．

（1）证明：；
（2）当为的中点，与平面所成的角为，求平面与平面所成的锐二面角的余弦值．
18. 已知双曲线左、右焦点为，，过的直线与双曲线交于，两点.
（1）若轴，求线段的长；
（2）若直线与双曲线的左、右两支相交，且直线交轴于点，直线交轴于点.
（i）若，求直线的方程；
（ii）若，恒在以为直径的圆内部，求直线的斜率的取值范围.
19. 已知是各项均为正整数的无穷递增数列，对于，设集合，设为集合中的元素个数，当时，规定.
（1）若，求，，的值；
（2）若，设的前项和为，求；
（3）若数列是等差数列，求数列的通项公式.