数学七年级下册（2024）11.2 一元一次不等式教课内容课件ppt

这是一份数学七年级下册（2024）11.2 一元一次不等式教课内容课件ppt，共18页。PPT课件主要包含了右两边均为整式，不相等，左边不是整式，x－7＞26，等式的性质，不等式的性质，只有一个解，一般有无数个解，x＝a，x≥－2等内容，欢迎下载使用。
1.理解和掌握一元一次不等式的概念；2.会用不等式的性质熟练地解一元一次不等式.(重点、难点）3.通过解一元一次不等式寻找整数解.(难点）
1.只有一个未知数；2.未知数的次数是1；3.不等号的两边都是整式.
只含有一个未知数，且含有未知数的式子都是整式，未知数的次数是1的不等式，称为一元一次不等式.
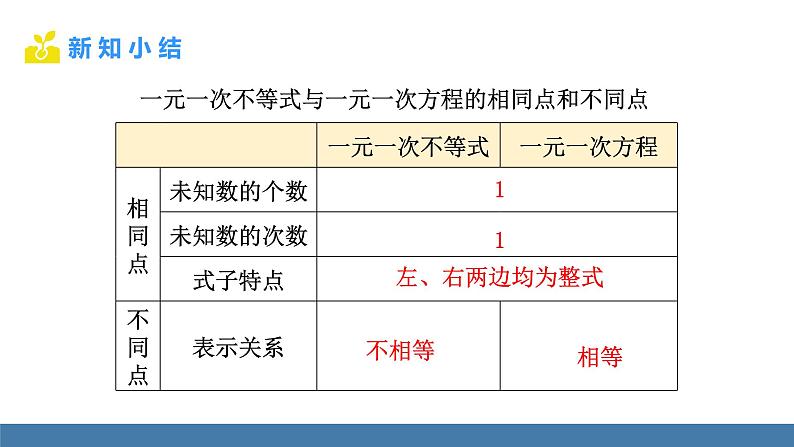
它与一元一次方程的定义有什么共同点吗？
一元一次不等式与一元一次方程的相同点和不同点
化简后是x2－x＜2x
例1 已知 是关于x的一元一次不等式，则a的值是________．
利用不等式的性质解不等式：
解：根据不等式的性质 1，不等式的两边加 7，不等号的方向不变，所以 x－7＋7＞26＋7，即 x＞33.
这个过程也可以看做“移项”
解：(2)去分母，得 3(x－5)＋24≥2(5x＋1).去括号，得 3x－15＋24≥10x＋2 .移项，得 3x－10x ≥ 2＋15－24 .合并同类项，得 －7x ≥ －7 .系数化为 1，得 x ≤ 1 .这个不等式的解集在数轴上的表示如图所示 .
思考 解一元一次不等式与解一元一次方程的步骤和依据有什么类似之处?
①去分母；②去括号；③移项；④合并同类项；⑤系数化为1.(对于解不等式，在去分母、系数化为1时，若两边同时乘(或除以)一个负数，则不等号的方向改变)
x＜a(x≤a)或x＞a(x≥a)
解：由方程的解的定义，把 x＝3 代入 ax＋12＝0 中， 得 a＝－4. 把a＝－4代入(a＋2)x＞－6中， 得－2x＞－6， 解得x＜3. 在数轴上表示如图： 其中正整数解有 1 和 2.
例3 已知方程 ax＋12＝0 的解是 x＝3，求关于 x 不等式（a＋2）x＞－6的解集，并在数轴上表示出来，其中正整数解有哪些？
求不等式的特殊解，先要准确求出不等式的解集，然后确定特殊解．在确定特殊解时，一定要注意是否包括端点的值，一般可以结合数轴，形象直观，一目了然．
1. 解下列不等式：
3. 解下列不等式，并把它们的解集在数轴上表示出来：
解：(1)原不等式的解集为x＜5，在数轴上表示为
(2)原不等式的解集为x≤－11，在数轴上表示为：
4. a≥1的最小正整数解是m,b≤8的最大正整数解是n,求关于x的不等式(m＋n)x＞18的解集．
解：因为a≥1的最小正整数解是m,所以m＝1. 因为b≤8的最大正整数解是n,所以n＝8.
把m＋n＝9代入不等式(m＋n)x＞18中，得 9x＞18，解得x＞2.
解得 x ≤ 6.
x≤6在数轴上表示如图所示.
所以，当x≤6时，代数式 x＋2的值大于或等于0.
由图可知，满足条件的正整数有 0,1,2,3,4,5,6.