江苏无锡市东林中学2024-2025学年七上数学第15周阶段性训练模拟练习【含答案】

这是一份江苏无锡市东林中学2024-2025学年七上数学第15周阶段性训练模拟练习【含答案】，共17页。

A．
B．
C．
D．
2．如果∠α和∠β互补，且∠α＞∠β，则下列表示∠β的余角的式子中：①90°﹣∠β；②∠α﹣90°；③180°﹣∠α；④（∠α﹣∠β）．正确的是（ ）
A．①②③④B．①②④C．①②③D．①②
3．A，B，C三个住宅区分别住有某公司职工20人、40人、10人，且这三个住宅区在一条大道上（A，B，C三点共线），如图所示，已知AB＝100米，BC＝200米，为了方便职工上下班，该公司的接送车打算在此区间内设一个停靠点，为使所有的人步行到停靠点的路程之和最小，那么该停靠点的位置应设在（ ）
A．点AB．点BC．点A，B之间D．点B，C之间
4．“君到姑苏来，人家尽枕河”，“小桥，流水，人家”描绘了一幅唯美的姑苏画卷．如图，在6个小正方形组成的平面图形上印有“小”“桥”“流”“水”“人”“家”，将其折叠成正方体纸盒，则“家”所在面的对面上的汉字是（ ）
A．小B．桥C．流D．水
5．在中国数学名著《九章算术》中，有这样一个问题：“今有共买牛，七家共出一百九十，不足三百三十；九家共出二百七十，盈三十．问家数、牛价各几何？”大意是：几家人凑钱合伙买牛，如果每7家共出190元，那么还缺少330元钱；如果每9家共出270元，又多了30元钱．问共有多少人家，每头牛的价钱是多少元？若设有x户人家，则可列方程为（ ）
A．
B．
C．
D．
二．填空题（共11小题）
6．图中平面展开图按虚线折叠成正方体后，相对面上两个数之和为5，则x+y＝ ．
7．如图，AB＝4cm，BC＝2cm，D为AC的中点，则BD的长是 cm．
8．数学上把关于x的代数式用记号f（x）来表示．当x＝a时，代数式的值用f（a）表示．例如代数式f（x）＝x2﹣x+1，当x＝4时，代数式的值为f（4）＝42﹣4+1＝13．已知代数式f（x）＝mx3﹣nx+3，若f（1）＝2024，则f（﹣1）的值为 ．
9．当x＝1时，代数式ax3+x2+bx的值为2024，当x＝﹣1时，代数式ax3+x2+bx的值为 ．
10．一件商品按成本价提高20%后标价，又以9折销售，售价为270元，这种商品的成本价是 元．
11．如图，将三个大小相同的正方形的一个顶点重合放置，那么∠1的度数为 ．
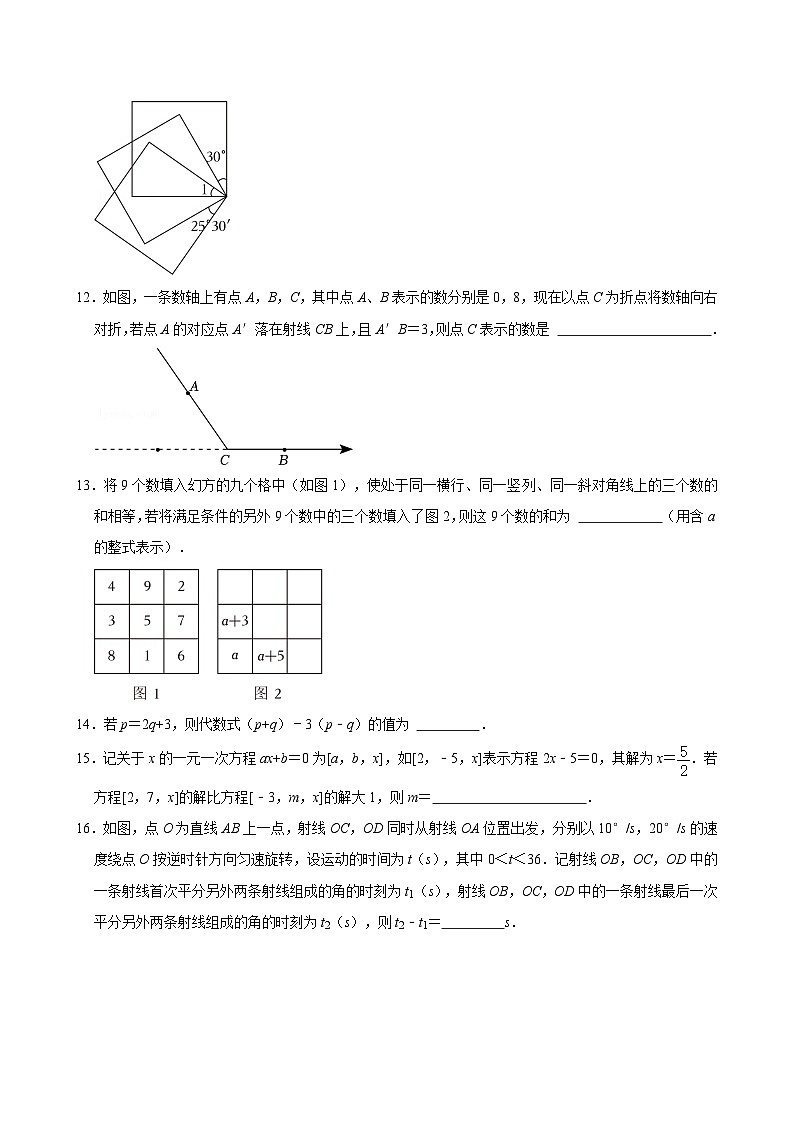
12．如图，一条数轴上有点A，B，C，其中点A、B表示的数分别是0，8，现在以点C为折点将数轴向右对折，若点A的对应点A′落在射线CB上，且A′B＝3，则点C表示的数是 ．
13．将9个数填入幻方的九个格中（如图1），使处于同一横行、同一竖列、同一斜对角线上的三个数的和相等，若将满足条件的另外9个数中的三个数填入了图2，则这9个数的和为 （用含a的整式表示）．
14．若p＝2q+3，则代数式（p+q）﹣3（p﹣q）的值为 ．
15．记关于x的一元一次方程ax+b＝0为[a，b，x]，如[2，﹣5，x]表示方程2x﹣5＝0，其解为x＝．若方程[2，7，x]的解比方程[﹣3，m，x]的解大1，则m＝ ．
16．如图，点O为直线AB上一点，射线OC，OD同时从射线OA位置出发，分别以10°/s，20°/s的速度绕点O按逆时针方向匀速旋转，设运动的时间为t（s），其中0＜t＜36．记射线OB，OC，OD中的一条射线首次平分另外两条射线组成的角的时刻为t1（s），射线OB，OC，OD中的一条射线最后一次平分另外两条射线组成的角的时刻为t2（s），则t2﹣t1＝ s．
三．解答题（共10小题）
17．如图，两直线AB、CD相交于点O，OE平分∠BOD，如果∠AOC：∠AOD＝7：11．
（1）求∠COE；
（2）如果∠COF＝125°，OE与OF有怎样的位置关系？为什么？
18．为促进电力资源的优化配置，某地居民用电实施峰谷计费．峰时段为8：00﹣21：00；谷时段为21：00﹣次日8：00．如表为该地某户居民11月份的电费账单的部分信息，设其中的峰时电量为x千瓦时，根据所给信息，解决下列问题．
（1）填空（用含x的代数式表示）：① ，② ，③ ；
（2）由题意，可列方程为 ；
（3）该账单中的峰时电量、谷时电量分别为多少千瓦时？
19．如图（1）已知数轴上点O表示原点，点M表示的数为12．动点A从原点出发，以每秒1个单位长度的速度沿数轴向右运动，到点M停止运动；动点E从M点出发，以每秒2个单位长度的速度沿数轴先运动到点O后立即以原速返回M，点A和点E同时出发，同时停止．设运动的时间为t秒．
（1）点A在数轴上表示的数为 ，点E在数轴上表示的数为 （用含t的代数式表示）；
（2）如图（2）数轴上从左到右依次是点A、B、E、F，线段AB＝2，EF＝4，在数轴上方作正方形ABCD与正方形EFGH，两个正方形随点A和点E运动，若两个正方形同时出发，求t为何值时，两个正方形的重叠部分面积为2？
20．已知关于x的方程与方程的解互为倒数，求2m2﹣4m+3的值．
21．根据最新版苏州市市民价格手册，苏州市对居民生活用电实行阶梯电价，居民阶梯电价按“年”为周期执行，即每年1月1日至12月31日为一周期，视为一年，执行标准如下：
已知2023年老李家用电2400千瓦时，交电费1200元；老王家交电费1524元．
（1）表中a的值为 ；
（2）求老王家2023年用电量；
（3）若2023年老张家用电的平均电价为0.6元/千瓦时，求老张家2023年的用电量．
22．如图，在数轴上A点表示数a，B点表示数b，AB表示A点和B点之间的距离，且a，b满足|a+1|+（b﹣3）2＝0．
（1）求A、B两点之间的距离；
（2）若在数轴上存在一点C，且AC＝4BC，求C点表示的数；
（3）若在原点O处放一挡板，一小球甲从点A处以1个单位/秒的速度向左运动；同时另一小球乙从点B处以2个单位/秒的速度也向左运动，在碰到挡板后（忽略球的大小，可看作一点）以原来的速度向相反的方向运动，设运动的时间为t（秒），求甲、乙两小球到原点的距离相等时经历的时间为 ．
23．若同一平面内三条射线OA，OB，OC有公共端点，且满足时，我们称射线OC是（OA，OB）的半角线，但射线OC不是（OB，OA）的半角线．
（1）如图1，已知AO⊥BO，垂足为O，∠AOE＝∠EOF＝30°，在射线OE，OF中，射线 是（OA，OB）的半角线；
（2）如图2，同一平面内，已知∠AOB＝45°，射线OC是（OA，OB）的半角线，求∠BOC；
（3）如图3，∠AOP＝45°，射线OC、OB同时从OP开始，分别以每秒5°和每秒3°的速度按逆时针方向绕点O旋转，当射线OC旋转一周时OC、OB同时停止运动，设旋转的时间为t（时间单位：s）．问t为何值时，射线OC是（OA，OB）的半角线．
24．如图，数轴上点A，B，C，O分别表示有理数a，b，c，0．
（1）若点B是线段AC的中点，且a＝3，c＝﹣5，则b＝ ；
（2）若点A在原点O右侧，点B，C在原点O左侧，且OA＞OB，化简：|a+b|+|b+c|﹣|a﹣c|．
25．杭州亚运会期间，某工厂接到一批亚运会纪念品生产任务，组委会要求6天内完成．若工厂安排10位工人生产，则6天后剩余1200套纪念品未生产；若安排15位工人生产，则恰好提前一天完成纪念品生产任务．问这批纪念品共有多少套，每位工人每天生产多少套纪念品？
26．如图，甲、乙两地位于一条平直的公路上，上午8：00，一辆出租车以80km/h的速度载客从甲地开往乙地，到达乙地后立即沿原路原速返回，上午8：30，一辆货车以40km/h的速度载货从乙地开往甲地，两车到达各自的目的地后停止运动．
（1）上午9：30，两车在途中迎面相遇，求甲、乙两地之间的距离．
（2）在（1）的条件下，设货车行驶的时间为t（h），当t为何值时，两车相距20km？
（3）根据（2）中数据，在货车行驶过程中，两车距离不超过20km的总时长为 h．
参考答案与试题解析
一．选择题（共5小题）
1．【解答】解：领奖台从正面看，是由三个矩形组成的，右边的矩形是最低的，中间的矩形是最高的，
故选：A．
2．【解答】解：∵∠α与∠β互补，
∴∠β＝180°﹣∠α，∠α＝180°﹣∠β，
∴90°﹣∠β表示∠β的余角，∴①正确；
∠α﹣90°＝180°﹣∠β﹣90°＝90°﹣∠β，∴②正确；
180°﹣∠α＝∠β，∴③错误；
（∠α﹣∠β）＝（180°﹣∠β﹣∠β）＝90°﹣∠β，∴④正确；
故选：B．
3．【解答】解：设停靠点的位置在x处，
所有的人步行到停靠点的路程之和＝20|x﹣A|+40|x﹣B|+10|x﹣C|，
∴当x在B点处，所有的人步行到停靠点的路程之和最小，
故选：B．
4．【解答】解：根据正方体表面展开图的“相间、Z端是对面”可知，人对流，桥对家，水对小，
故选：B．
5．【解答】解：设有x户人家，则．
故选：A．
二．填空题（共11小题）
6．【解答】解：由图可知：
2与x相对，4与y相对，
∴2+x＝5，4+y＝5，
∴x＝3，y＝1，
∴x+y＝3+1＝4，
故答案为：4．
7．【解答】解：∵AB＝4cm，BC＝2cm，
∴AC＝AB+BC＝4+2＝6（cm），
∵D为AC的中点，
∴CD＝AC＝3（cm），
∴BD＝CD﹣BC＝3﹣2＝1（cm），
故答案为：1．
8．【解答】解：∵f（1）＝m﹣n+3＝2024，
∴m﹣n＝2021．
∴f（﹣1）＝﹣m+n+3
＝﹣（m﹣n）+3
＝﹣2021+3
＝﹣2018．
故答案为：﹣2018．
9．【解答】解，由题意得a+1+b＝2024，
则a+b＝2023，
当x＝﹣1时，
ax3+x2+bx
＝﹣a+1﹣b
＝﹣（a+b）+1
＝﹣2023+1
＝﹣2022，
故答案为：﹣2022．
10．【解答】解：设这件商品的成本价为x元，
由题意得：0.9x（1+20%）＝270，
解得：x＝250．
故答案为：250元．
11．【解答】解：如图：
∵∠1+∠2+∠3＝90°，∠1+∠3+25°30'＝90°，
∴∠2＝25°30'，
又∵∠1+∠2+30°＝90°，
∴∠1＝90°﹣30°﹣25°30'＝34°30′．
故答案为：34°30′．
12．【解答】解：设点C表示的数是x，
当点A'在线段AB上时，如图，
∵点A、B表示的数分别是0，8，
∴AC＝A'C＝x，AB＝8，A′B＝3，
∴2x+3＝8，
解得x＝；
当点A'在线段AB的延长线上时，如图，
∵点A、B表示的数分别是0，8，
∴AC＝A'C＝x，AB＝8，A′B＝3，
∴2x＝8+3，
解得，
综上，点C表示的数是或，
故答案为：或．
13．【解答】解：如图所示：
a+2a+3﹣x+3a﹣2x+6＝a+a+5+x，
解得x＝a+1，
a+a+5+x＝2a+5+a+1＝3a+6，
3（3a+6）＝9a+18．
故答案为：9a+18．
14．【解答】解：∵p＝2q+3，
∴2q﹣p＝﹣3，
原式＝（p+q）﹣3（p﹣q）
＝p+q﹣3p+3q
＝4q﹣2p
＝2（2q﹣p）
＝2×（﹣3）
＝﹣6．
故答案为：﹣6．
15．【解答】解：方程[2，7，x]＝2x+7＝0的解为，
方程[﹣3，m，x]＝﹣3x+m＝0解为．
则．
故答案为：．
16．【解答】解：第一次平分，即OD平分∠BOC：180﹣20t＝10t，
解得t＝6s，
最后一次平分，即OC靠近OA，OD平分∠BOC：10t﹣180＝2（20t﹣540），
解得t2＝30s，
∴t2﹣t1＝30﹣6＝24s，
故答案为：24．
三．解答题（共10小题）
17．【解答】解：（1）∵∠AOC：∠AOD＝7：11．∠AOC+∠AOD＝180°，
∴∠AOC＝180°×＝70°，∠AOD＝＝110°，
∵OE平分∠BOD，
∴∠BOE＝∠DOE＝∠BOD，
∵∠AOC＝∠BOD＝70°，∠AOD＝∠BOC＝110°，
∴∠BOE＝35°，
∴∠COE＝∠BOC+∠BOE＝145°；
（2）OE⊥OF，理由：
∵∠COF＝125°，
∴∠DOF＝180°﹣125°＝55°，
又∵∠DOE＝35°，
∴∠EOF＝∠DOF+∠DOE＝90°，
∴OE⊥OF．
18．【解答】解：（1）峰时费用为：0.56x（元），
谷时电量为：（350﹣x）元，
谷时费用为：0.36（350﹣x）元；
故答案为：350﹣x，0.56x，0.36（350﹣x）；
（2）根据题意得：0.56x+0.36（350﹣x）＝160；
故答案为：0.56x+0.36（350﹣x）＝160；
（3）解（2）中的方程：0.56x+0.36（350﹣x）＝160，
解得：x＝170，
则350﹣x＝180，
∴该账单中的峰时电量为170千瓦时，谷时电量180千瓦时．
19．【解答】解：（1）由题意知点A表示的数为t，
当0≤t≤6时，点E表示的数为12﹣2t，
当6＜t≤12时，点E表示的数为2t﹣12，
∴点E表示的数为|2t﹣12|，
故答案为：t，|2t﹣12|；
（2）分情况讨论：
当0≤t≤6时，有两种情况，
∵正方形ABCD边长为2，
∴若重叠部合面积为2，则正方形ABCD有一半在重叠部分，
当0＜t＜6时有两种情况，
①A在E左侧，此时AE＝1，
A表示的数为t，E表示的数为12﹣2t，
∴AE＝12﹣2t﹣t＝12﹣3t＝1，
解得t＝，
②A在E右侧，此时AE＝3，
AE＝t﹣（12﹣2t）＝3t﹣12＝3，
解得t＝5；
当6＜t≤12时，分两种情况，
①点A在E右侧，此时AE＝3，
AE＝t﹣（2t﹣12）＝12﹣t＝3，
解得t＝9，
②点A在E左侧，此时AE＝1，
AE＝2t﹣12﹣t﹣1＝1，
解得t＝13＞12（舍去），
综上，当t为9秒，秒或5秒时重叠部分面积为2．
20．【解答】解：解方程，得x＝﹣；
解方程，得x＝，
∵﹣×＝1，
∴m＝﹣1．
当m＝﹣1时，2m2﹣4m+3＝2+4+3＝9．
21．【解答】解：（1）2023年老李家用电2400千瓦时，2400＜2760，则为第一档，
可得方程：2400a＝1200，
解得：a＝0.5，
故答案为：0.5．
（2）解：设老王家2023年用电量为x千瓦时，
∵2760×0.5＝1380（元），1380+（4800﹣2760）×0.6＝2604（元），1380＜1524＜2604，
∴2760＜x＜4800，
根据题意，得：1380+（x﹣2760）×0.6＝1524，
解得：x＝3000，
答：老王家2023年用电量为3000千瓦时．
（3）解：若用电量为4800千瓦时，电费为2604元，则＜0.6，
∴2023年老张家用电量超过了4800千瓦时，
设老张家2023年用电量为y千瓦时，
根据题意，得：2604+（y﹣4800）×0.8＝0.6y，
解得：y＝6180，
答：老张家2023年用电量为6180千瓦时．
22．【解答】解：（1）∵|a+1|+（b﹣3）2＝0，且|a+1|≥0，（b﹣3）2≥0，
∴a+1＝0，b﹣3＝0，
∴a＝﹣1，b＝3，
∴AB的距离＝|b﹣a|＝4；
（2）设数轴上点C表示的数为c，
∵AC＝4BC，
∴|c﹣a|＝4|c﹣b|，即|c+1|＝4|c﹣3|．
∵AC＝4BC＞BC，
∴点C不可能在线段BA的延长线上，则C点可能在线段AB上和线段AB的延长线上．
①当C点在线段AB上时，则有﹣1≤c≤3，
得c+1＝4（3﹣c），
解得；
②当C点在线段AB的延长线上时，则有c＞3，
得c+1＝4（c﹣3），
解得．
故当AC＝4BC时，或；
（3）设运动时间为t秒，
当小球乙向左运动时，即小球乙没有碰到挡板时，
∵甲、乙两小球到原点的距离相等，
∴1+t＝3﹣2t，
解得；
当小球乙向右运动时，即小球乙碰到挡板后，
∵甲、乙两小球到原点的距离相等，
∴1+t＝2t﹣3，
解得t＝4；
综上，甲、乙两小球到原点的距离相等时经历的时间为秒或4秒，
故答案为：秒或4秒．
23．【解答】（1）根据半角线的定义，可得OE是是（OA，OB）的半角线，
故答案为：OE；
（2）①当射线OC在∠AOB的外部时，如图1，
∵∠AOB＝45°，射线OC是（OA，OB）的半角线，
∴，
∴，
即，
解得∠BOC＝90°；
②当射线OC在∠AOB的内部时，如图2，
∵∠AOB＝45°，射线OC是（OA，OB）的半角线，
∴，
∴，即，
解得∠BOC＝30°，
综上所述，∠BOC＝90°或30°；
（3）①当0＜t≤9时，射线OC、OB都在∠AOP内部，如图3，
∠AOC＝45°﹣5°•t，∠BOC＝5°•t﹣3°•t＝2°•t，
∵射线OC是（OA，OB）的半角线，
∴＝1°•t，
∴45°﹣5°t＝1°•t，
解得；
②当9＜t≤45时，射线OC在∠AOP外部，射线OB在∠AOP内部，如图4，
∠AOC＝5°•t﹣45°＝5°•t﹣45°，∠BOC＝5°•t﹣3°•t＝2°•t，
∵射线OC是（OA，OB）的半角线，射线OC、OB都在∠AOP内部，
∴＝1°•t，
∴5°•t﹣45°＝1°•t，
解得；
③当45＜t≤72时，射线OC、OB都在∠AOP外部，如图5，
∠AOC＝405°﹣5°•t，∠BOC＝2°•t，
∵射线OC是（OA，OB）的半角线，
∴＝1°•t，
∴405°﹣5°•t＝1°•t，
解得．
综上所述，t的值为或或时，射线OC是（OA，OB）的半角线．
24．【解答】解：（1），
故答案为：﹣1．
（2）由题知：a＞0＞b＞c，|a|＞|b|，|c|＞|a|，
∴a+b＞0，b+c＜0，a﹣c＞0，
则|a+b|＝a+b，|b+c|＝﹣b﹣c，|a﹣c|＝a﹣c，
∴|a+b|+|b+c|﹣|a﹣c|＝a+b﹣b﹣c﹣a+c＝0．
25．【解答】解：设每位工人每天生产x套纪念品，
由题意得：6×10x+1200＝15x×（6﹣1），
解得x＝80，
6×10x+1200＝6000（套），
答：这批纪念品共有6000套，每位工人每天生产80套纪念品．
26．【解答】解：（1）s＝1.5×80+40×1＝160km，
答：甲、乙两地之间的距离为160千米；
（2）设货车行驶时间为t，甲点为原点，则乙点表示的数为160，
出租车到达乙地前表示的数为：80（t+）＝80t+40 （t≤1.5），
到达乙地后表示的数为：160﹣[80（t+）﹣160]＝280﹣8t（1.5＜t≤3.5），
货车表示的数为：160﹣40t；
①相遇前：|（160﹣40t）﹣（80t+40）|＝20，解得：t＝或t＝，
②相遇后：|280﹣80t﹣（160﹣40t）|＝20，解得：t＝2.5或t＝3.5，
∴当t为 ，两车相距 20km；
（3）两车距离不超过 20km的总时长为：，故答案为：．户主
***
用电户号
******
合计金额
160元
合计电量
350千瓦时
抄送周期
﹣
备注：合计电量＝峰时电量+谷时电量
单价（元）
计费数量（千瓦时）
金额（元）
峰时电量
0.56
x
②
谷时电量
0.36
①
③
档次
阶梯分档电量
电价（元/千瓦时）
第1档
不超过2760千瓦时的部分
a
第2档
超过2760千瓦时但不超过4800千瓦时的部分
0.6
第3档
超过4800千瓦时的部分
a+0.3
题号
1
2
3
4
5
答案
A
B
B
B
A