初中数学湘教版（2024）八年级上册第2章 三角形2.5 全等三角形一课一练

这是一份初中数学湘教版（2024）八年级上册第2章 三角形2.5 全等三角形一课一练，共7页。
一．选择题（每小题3分，共30分）
1．如图，在△ABC和△ADE中，AB＝AD，AC＝AE，添加下列条件，不一定能得到△ABC≌△ADE的是（ ）
A．BC＝DEB．∠BAC＝∠DAEC．∠BAD＝∠CAED．∠C＝∠E
2．根据下列已知条件，能画出唯一的△ABC的是（ ）
A．AB＝3cm，AC＝5cm，∠B＝90° B．BC＝8cm，∠A＝60°
C．AB＝3cm，BC＝5cm，∠C＝50°D．∠A＝60°，∠B＝70°，∠C＝50°

第1题图 第3题图 第4题图 第6题图
3．工人师傅常用角尺平分一个任意角，做法是：如图在∠AOB的边OA、OB上分别取OM＝ON，移动角尺，使角尺的两边相同的刻度分别与M、N重合，得到∠AOB的平分线OP，做法中用到三角形全等的判定方法是（ ）
A．SSSB．SASC．ASAD．HL
4．如图，BE＝CF，AE⊥BC，DF⊥BC，要根据“HL”证明Rt△ABE≌Rt△DCF，则还需要添加一个条件是（ ）
A．AE＝DFB．∠A＝∠DC．∠B＝∠CD．AB＝DC
5．下列各选项中的两个直角三角形不一定全等的是（ ）
A．两条直角边对应相等的两个直角三角形
B．两个锐角对应相等的两个直角三角形
C．斜边和一条直角边对应相等的两个直角三角形
D．有一个锐角及这个锐角的对边对应相等的两个直角三角形全等
6．如图，AB＝AC，BD＝CD，∠BAC＝70°，∠ADB＝120°，则∠C的度数为（ ）
A．25°B．30°C．35°D．55°
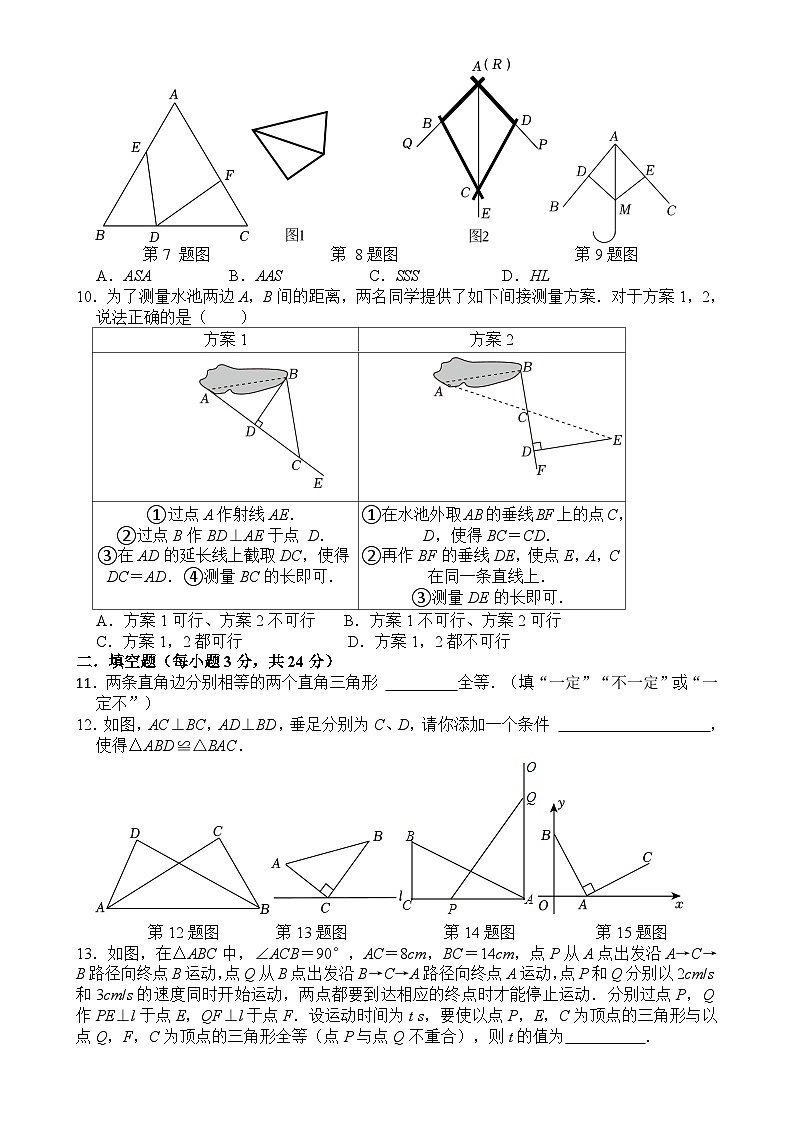
7．如图，△ABC中，∠B＝∠C，BD＝CF，BE＝CD，∠EDF＝α，则下列结论正确的是（ ）
A．2α﹣∠A＝90°B．2α+∠A＝180°
C．α+∠A＝90°D．α+∠A＝180°
8．图1是数学实验课上小哲做的角平分仪，其工作原理如图2，其中AB＝AD，BC＝DC，将仪器上的点A与∠PRQ的顶点R重合，调整AB和AD，使它们分别落在角的两边上，则射线AE就是∠PRQ的平分线．此角平分仪作图所运用的数学知识是（ ）
A．SSSB．SASC．ASAD．AAS
9．如图是雨伞在开合过程中某时刻的截面图，伞骨AB＝AC，点D，E分别是AB，AC的中点，DM，EM是连接弹簧和伞骨的支架，且DM＝EM，已知弹簧M在向上滑动的过程中，总有△ADM≌△AEM，其判定依据是（ ）
第7 题图 第 8题图 第9题图
A．ASAB．AASC．SSSD．HL
10．为了测量水池两边A，B间的距离，两名同学提供了如下间接测量方案．对于方案1，2，说法正确的是（ ）
A．方案1可行、方案2不可行 B．方案1不可行、方案2可行
C．方案1，2都可行 D．方案1，2都不可行
二．填空题（每小题3分，共24分）
11．两条直角边分别相等的两个直角三角形 全等．（填“一定”“不一定”或“一定不”）
12．如图，AC⊥BC，AD⊥BD，垂足分别为C、D，请你添加一个条件 ，使得△ABD≌△BAC．
第12题图 第13题图 第14题图 第15题图
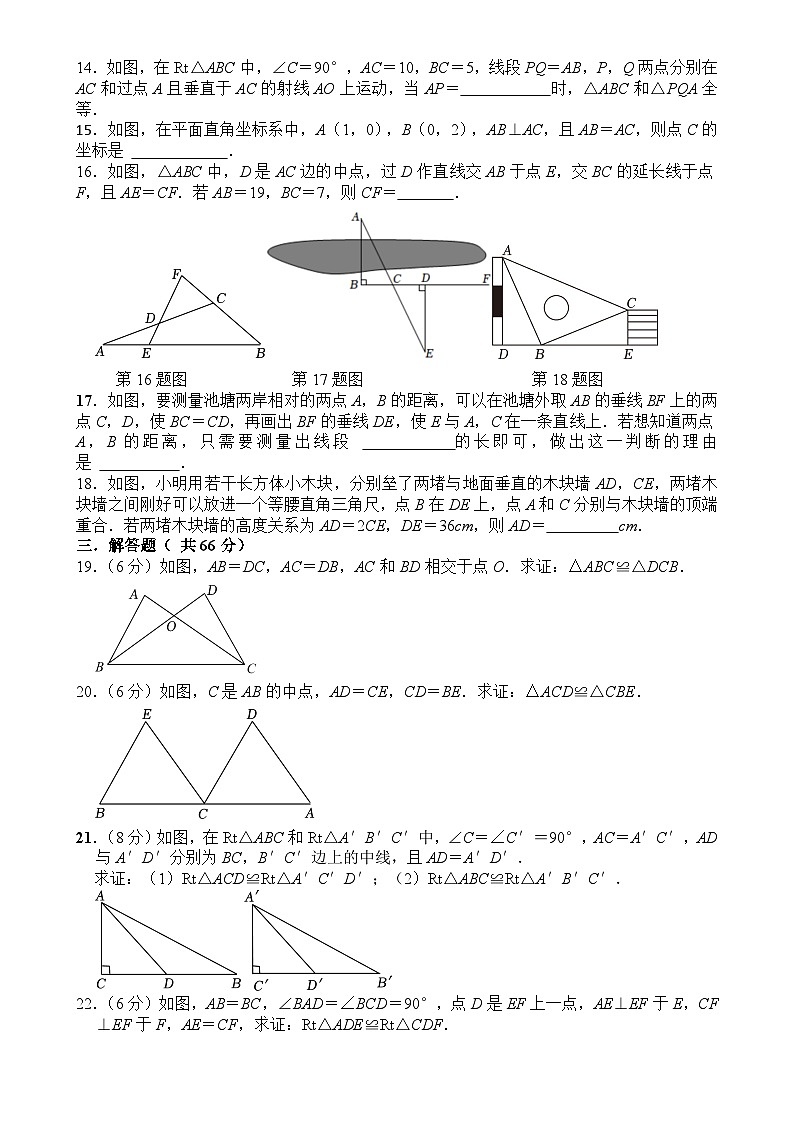
13．如图，在△ABC中，∠ACB＝90°，AC＝8cm，BC＝14cm，点P从A点出发沿A→C→B路径向终点B运动，点Q从B点出发沿B→C→A路径向终点A运动，点P和Q分别以2cm/s和3cm/s的速度同时开始运动，两点都要到达相应的终点时才能停止运动．分别过点P，Q作PE⊥l于点E，QF⊥l于点F．设运动时间为t s，要使以点P，E，C为顶点的三角形与以点Q，F，C为顶点的三角形全等（点P与点Q不重合），则t的值为 ．
14．如图，在Rt△ABC中，∠C＝90°，AC＝10，BC＝5，线段PQ＝AB，P，Q两点分别在AC和过点A且垂直于AC的射线AO上运动，当AP＝ 时，△ABC和△PQA全等．
15．如图，在平面直角坐标系中，A（1，0），B（0，2），AB⊥AC，且AB＝AC，则点C的坐标是 ．
16．如图，△ABC中，D是AC边的中点，过D作直线交AB于点E，交BC的延长线于点F，且AE＝CF．若AB＝19，BC＝7，则CF＝ ．
第16题图 第17题图 第18题图
17．如图，要测量池塘两岸相对的两点A，B的距离，可以在池塘外取AB的垂线BF上的两点C，D，使BC＝CD，再画出BF的垂线DE，使E与A，C在一条直线上．若想知道两点A，B的距离，只需要测量出线段 的长即可，做出这一判断的理由是 ．
18．如图，小明用若干长方体小木块，分别垒了两堵与地面垂直的木块墙AD，CE，两堵木块墙之间刚好可以放进一个等腰直角三角尺，点B在DE上，点A和C分别与木块墙的顶端重合．若两堵木块墙的高度关系为AD＝2CE，DE＝36cm，则AD＝ cm．
三．解答题（ 共66分）
19．（6分）如图，AB＝DC，AC＝DB，AC和BD相交于点O．求证：△ABC≌△DCB．
20．（6分）如图，C是AB的中点，AD＝CE，CD＝BE．求证：△ACD≌△CBE．
21．（8分）如图，在Rt△ABC和Rt△A′B′C′中，∠C＝∠C′＝90°，AC＝A′C′，AD与A′D′分别为BC，B′C′边上的中线，且AD＝A′D′．
求证：（1）Rt△ACD≌Rt△A′C′D′；（2）Rt△ABC≌Rt△A′B′C′．
22．（6分）如图，AB＝BC，∠BAD＝∠BCD＝90°，点D是EF上一点，AE⊥EF于E，CF⊥EF于F，AE＝CF，求证：Rt△ADE≌Rt△CDF．
23．（6分）如图，CD⊥AB于D点，BE⊥AC于E点，BE，CD交于O点，且AO平分∠BAC．
求证：OB＝OC．
24．（8分）如图，在四边形ABCD中，AB＝AD，BC＝DC，E为AC上的一点．
求证：（1）AC平分∠DAB；
（2）BE＝DE．
25．（8分）如图，CA＝CD，∠BCE＝∠ACD，BC＝EC．
（1）求证：AB＝DE；
（2）若∠A＝25°，∠E＝35°，求∠ECD的度数．
26．（8分）（1）如图1所示的折叠凳的设计所运用的数学原理是什么？
（2）图2是折叠凳撑开后的侧面示意图（木条等材料的宽度忽略不计），其中凳腿AB和CD的长度相等，交点O是它们的中点，折叠凳的宽AD为38cm，则BC的长度是多少？
27．（10分）八年级数学兴趣小组开展了测量学校教学楼高度AB的实践活动，测量方案如下表：
请你根据兴趣小组测量方案及数据，计算教学楼高度AB的值．
参考答案
1-5 .DAAD B 6-10 A B AC C
11．一定12．BC＝AD（答案不唯一）．13． 6或8．14.5或10．15.（3，1） 16.6
17.ED，ASA 18.24
19．证明：由题意可知，AB＝DC，AC＝DB，BC＝CB，。在△ABC和△DCB中，
，∴△ABC≌△DCB（SSS）．
20．证明：∵C是AB的中点，∴AC＝BC，∵AD＝CE，CD＝BE，在△ACD与△CBE中，
，∴△ACD≌△CBE（SSS）．
21．证明：（1）∵∠C＝∠C′＝90°，∴△ACD和△A′C′D′都是直角三角形，
在Rt△ACD和Rt△A′C′D′中，，∴Rt△ACD≌Rt△A′C′D′（HL）；
（2）∵Rt△ACD≌Rt△A′C′D′，∴CD＝C′D′，∵AD与A′D′分别为BC，B′C′边上的中线，∴CB＝C′B′＝2CD，在Rt△ABC和Rt△A′B′C′中，
，∴Rt△ABC≌Rt△A′B′C′（SAS）．
22．解：连接BD，∵∠BAD＝∠BCD＝90°，在Rt△ABD和Rt△CBD中，，∴Rt△ABD≌Rt△CBD（HL），∴AD＝CD，∵AE⊥EF于E，CF⊥EF于F，
∴∠E＝∠F＝90°，在Rt△ADE和Rt△CDF中，，∴Rt△ADE≌Rt△CDF（HL）．
23．证明：∵BE⊥AC，CD⊥AB，∴∠ADC＝∠BDC＝∠AEB＝∠CEB＝90°．
∵AO平分∠BAC，∴∠1＝∠2．在△AOD和△AOE中，，∴△AOD≌△AOE（AAS）．∴OD＝OE．在△BOD和△COE中，，∴△BOD≌△COE（ASA）．
∴OB＝OC．
24．证明：（1）在△ADC和△ABC中，∴△ADC≌△ABC（SSS），∴∠BAE＝∠DAE，∴AC平分∠DAB；（2）在△ABE和△ADE中，∴△ABE≌△ADE（SAS），∴BE＝DE．
25.（1）证明：∵∠BCE＝∠ACD，∴∠BCE+∠ACE＝∠ACD+∠ACE，∴∠ACB＝∠DCE，
在△ACB和△DCE中，，∴△ACB≌△DCE（SAS），∴AB＝DE．
（2）解：由（1）得△ACB≌△DCE，∴∠A＝∠D＝25°，∵∠E＝35°，∴∠ECD＝180°﹣∠D﹣∠E＝180°﹣25°﹣35°＝120°，∴∠ECD的度数是120°．
25.解：（1）这种设计所运用的数学原理是三角形具有稳定性；（2）AB和CD的长度相等，交点O是它们的中点，折叠凳的宽AD为38cm，∴AO＝BO，CO＝DO，
在△AOD和△BOC中，，∴△AOD≌△BOC（SAS），∴BC＝AD＝38cm．
方案1
方案2


①过点A作射线AE．
②过点B作BD⊥AE于点 D．
③在AD的延长线上截取DC，使得DC＝AD．④测量BC的长即可．
①在水池外取AB的垂线BF上的点C，D，使得BC＝CD．
②再作BF的垂线DE，使点E，A，C在同一条直线上．
③测量DE的长即可．
课题
测量学校教学楼高度AB
测量工具
测角仪、皮尺等
测量方案示意图

测量步骤
（1）在教学楼外，选定一点C；
（2）测量教学楼顶点A视线AC与地面夹角∠ACB；
（3）测BC的长度；
（4）放置一根与BC长度相同的标杆DE，DE垂直于地面；
（5）测量标杆顶部E视线与地面夹角∠ECD．
测量数据
∠ACB＝68.2°，∠ECD＝21.8°，BC＝DE＝2.5m，CD＝12m