第六章 几何图形初步 小结与复习课件

这是一份第六章 几何图形初步 小结与复习课件，共22页。
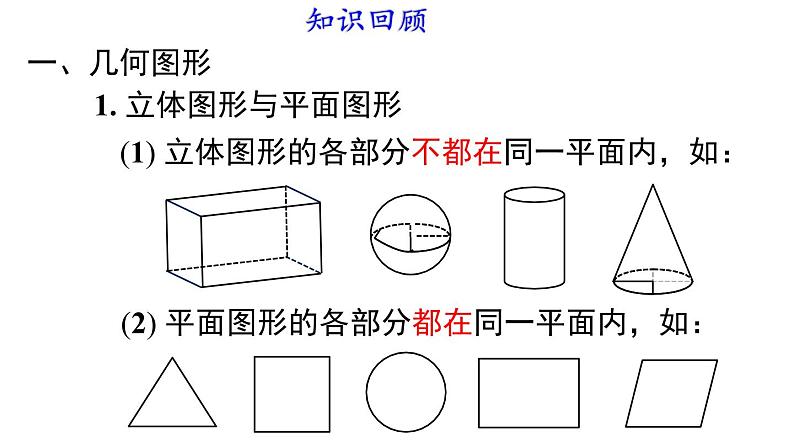
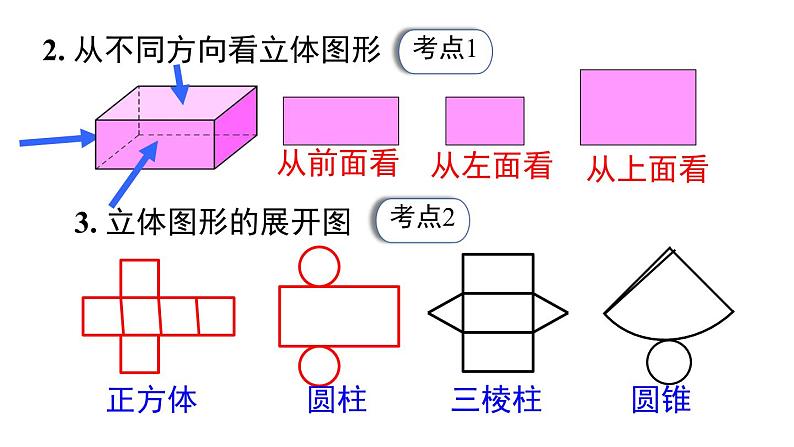
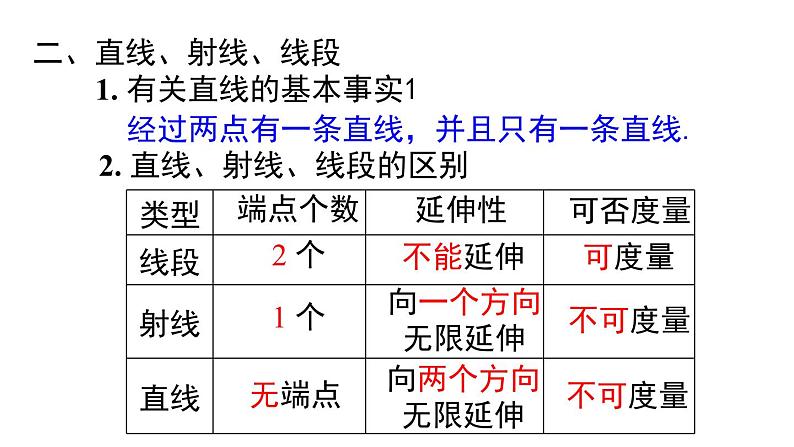
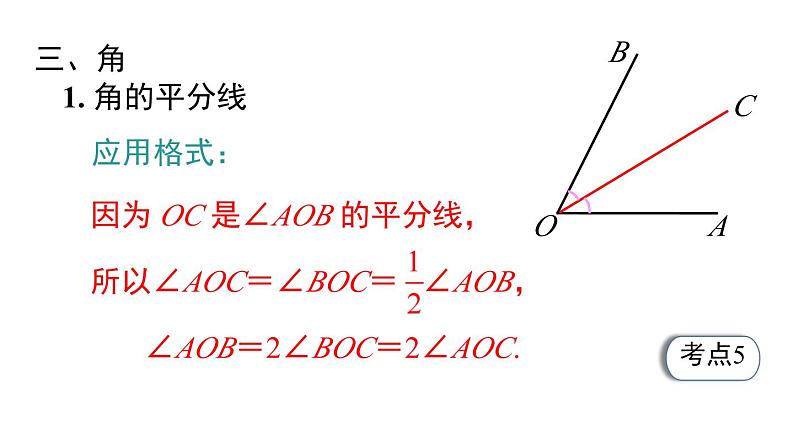
小结与复习第六章 几何图形初步一、几何图形1. 立体图形与平面图形 (1) 立体图形的各部分不都在同一平面内，如： (2) 平面图形的各部分都在同一平面内，如：知识回顾2. 从不同方向看立体图形3. 立体图形的展开图正方体圆柱三棱柱圆锥从前面看从左面看从上面看4. 点、线、面、体之间的联系(1) 体是由 围成，面与面相交成 ，线与线相交成 ；(2) 点动成线、线动成面、面动成体.面点线二、直线、射线、线段1. 有关直线的基本事实1经过两点有一条直线，并且只有一条直线.2. 直线、射线、线段的区别端点个数2 个不能延伸延伸性可否度量可度量1 个向一个方向无限延伸不可度量无端点向两个方向无限延伸不可度量3. 基本作图 (1) 作一线段等于已知线段； (2)利用尺规作图作一条线段等于两条线段的和、差.5. 有关线段的基本事实2：两点之间，线段最短.4. 线段的中点应用格式：6. 连接两点的线段的长度，叫做这两点间的距离.1. 角的平分线C应用格式：三、角2. 余角和补角(1) 定义 ① 如果两个角的和等于 90° (直角)，就说这 两个角互为余角 (简称为两个角互余). ② 如果两个角的和等于 180° (平角)，就说这 两个角互为补角 (简称为两个角互补).(2) 性质 ① 同角 (等角) 的余角相等. ② 同角 (等角) 的补角相等.例1 如图所示的立体图形从上面看到的图形是 ( )A. B. C. D.C1. 一个几何体由大小相同的小立方块搭成，从上面观察这个几何体，看到的形状如图所示，其中小正方形中的数字表示在该位置小立方块的个数，则从正面看该几何体的形状图为 ( )A. B. C. D.A24132例2 根据下列多面体的平面展开图，填写多面体的名称： (1)________，(2)_______，(3)________.长方体三棱柱三棱锥(1) (2) (3)2. 如图是一个正方体表面展开图，则原正方体中与“全”字所在面相对的面的字是 ；若从前面看正方体是“文”字，则后面看是 字.市全国文明城市城例3 如图，C 为线段 AB 上一点，点 D 为 BC 的中点，且 AB = 10 cm，BC = 4 cm.(1) 图中共有 条线段.(2) 求 AD 的长.6(2)解：因为点 D 为 BC 的中点，且 BC = 4 cm，因为 AB = 10 cm，所以 AD = AB - BD = 10 - 2 = 8 cm.3. 如图，已知 C 为线段 AB 的中点，D 在线段 CB 上. 若 DA = 6，DB = 4，则 CD =_____.1641054. 点 C 是线段 AB 上的三等分点，D 是线段 AC 的中点，若 AB = 6，则 BD 的长为_____.5或4652162424例4 如图，从 A 到 B 有多条道路，人们通常会走中间的直路，而不走其他的路，这其中的道理是 .两点之间，线段最短AB5. 如图，在 A 点有一只壁虎，要沿着圆柱体的表面 爬到 B 点去吃蚊子. 请画出壁虎在圆柱体表面爬 行的最短路线.A例5 如图，点 B 在点 O 的北偏东 60° 方向上，∠BOC = 110°，则点 C 在点 O 的 ( )A. 西偏北 60° 方向上B. 北偏西 40° 方向上C. 北偏西 50° 方向上D. 西偏北 50° 方向上CBOC北东6. 如图，将一张长方形纸片 ABCD 沿对角线 BD 折叠后，点 C 落在点 E 处，连接 BE 交 AD 于 F，再将三角形 DEF 沿 DF 折叠后，点 E 落在点 G 处，若 DG 刚好平分∠ADB，那么∠ADB 的度数是 ( )A. 18° B. 20°C. 36° D. 45°C3x+2x=90例5 如图，点 O 是直线 AB 上任一点，射线 OD 和射线 OE 分别平分∠AOC 和∠BOC.(1) 填空：与∠BOD 互补的角有 ；(2) 当 ∠BOE = α° 时，∠DOE = °.AOBCDE∠AOD 和∠COD907. 若∠A = 56°20′，则∠A 余角的大小是 ( )A. 34°40′ B. 33°40′ C. 124°40′ D. 123°40′8. (甘肃平凉期末) 已知∠α 的补角比∠α 大 30°， 则∠α =_____°.B75