福建省厦门市思明区大同中学2023-2024学年九年级上学期第二次月考数学试题（原卷版）-A4

这是一份福建省厦门市思明区大同中学2023-2024学年九年级上学期第二次月考数学试题（原卷版）-A4，共6页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1. 下列图形是我国国产品牌汽车的标识，这些汽车标识中，既是轴对称图形又是中心对称图形的是（ ）
A. B. C. D.
2. 将抛物线通过一次平移可得到抛物线，对这一平移过程描述正确的是（ ）
A. 向上平移5个单位长度B. 向下平移5个单位长度
C. 向左平移5个单位长度D. 向右平移5个单位长度
3. 下列事件中，是随机事件的是（ ）
A. 投掷一枚质地均匀的骰子，朝上一面的点数小于7
B. 在一个只装了红球的袋子里，摸出一个白球
C. 在一副扑克牌中抽出一张，抽出牌是黑桃6
D. 画一个三角形，其内角和是
4. 正多边形的中心角为，则正多边形的边数是（ ）
A. 4B. 6C. 8D. 12
5. 若的半径是3，点P到圆心O的距离是，那么点P与的关系是（ ）
A. 点P在上B. 点P在内C. 点P在外D. 无法确定
6. 有x支球队参加篮球比赛，共比赛了45场，每两队之间都比赛一场，则下列方程中符合题意的是（ ）
A. B. C. D.
7. 如图，四边形ABCD内接于⊙O，，则∠AOC的度数是（ ）
A. 70°B. 110°C. 135°D. 140°
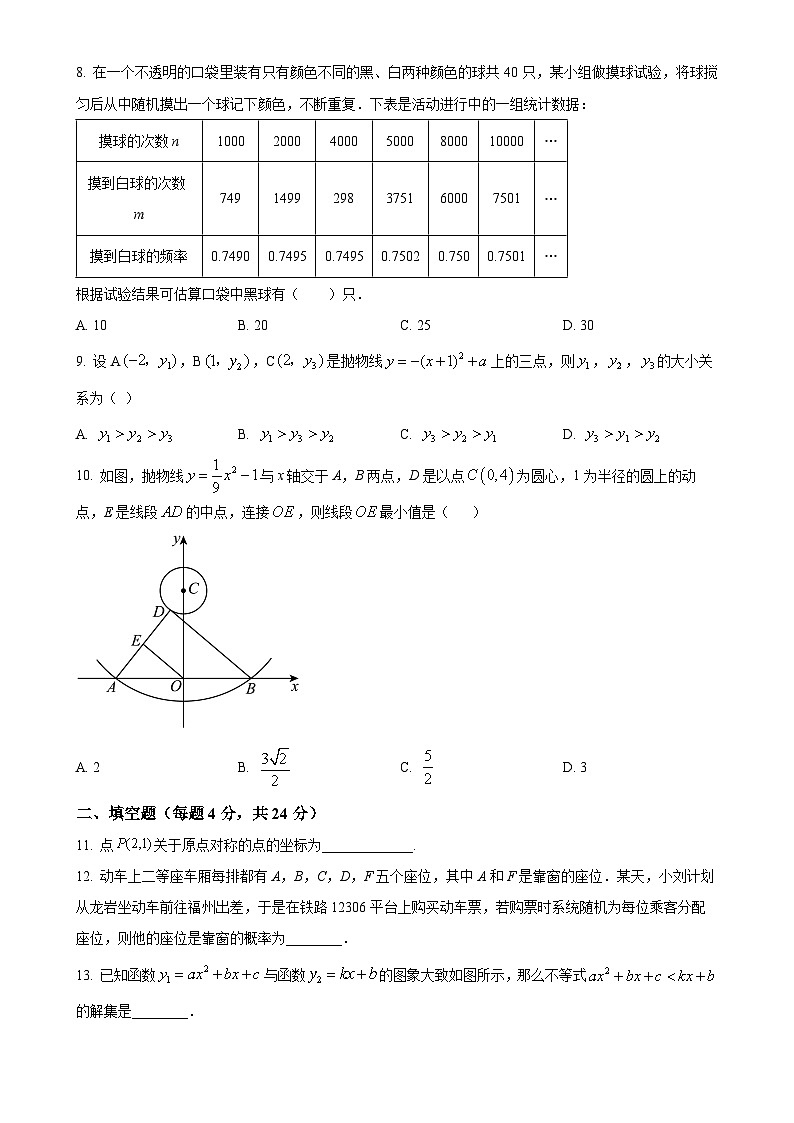
8. 在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共40只，某小组做摸球试验，将球搅匀后从中随机摸出一个球记下颜色，不断重复．下表是活动进行中的一组统计数据：
根据试验结果可估算口袋中黑球有（ ）只．
A. 10B. 20C. 25D. 30
9. 设A，B，C是抛物线上的三点，则，，的大小关系为（ ）
A. B. C. D.
10. 如图，抛物线与x轴交于A，B两点，D是以点为圆心，1为半径的圆上的动点，E是线段的中点，连接，则线段最小值是（ ）

A. 2B. C. D. 3
二、填空题（每题4分，共24分）
11. 点关于原点对称的点的坐标为_____________.
12. 动车上二等座车厢每排都有A，B，C，D，F五个座位，其中A和F是靠窗的座位．某天，小刘计划从龙岩坐动车前往福州出差，于是在铁路12306平台上购买动车票，若购票时系统随机为每位乘客分配座位，则他的座位是靠窗的概率为________．
13. 已知函数与函数的图象大致如图所示，那么不等式的解集是________．
14. 掷实心球是福建省中考体育考试的抽选考项目．实心球行进路线是一条抛物线，行进高度与水平距离，抛出时起点处高度为，当水平距离为时，实心球行进至最高点处，则行进高度与水平距离的关系式是________．
15. 如图，在半径为4，圆心角为的扇形内，以为直径作半圆，交弦于点D，则阴影部分的面积是________（结果保留π）．

16. 如图，矩形中，，，点是线段上的一个动点，将线段绕点逆时针旋转得到，过F作于点G，连接，取的中点H，连接，．点在运动过程中，下列结论：①；②当点H和点G互相重合时，；③平分；④．正确的是______．

三、解答题（共86分）
17 解方程：
（1）；
（2）．
18. 如图，在平面直角坐标系中，，，若绕点O逆时针旋转90°后，得到（对应点是，B对应点是）．
（1）画出，并直接写出的坐标；
（2）求旋转过程中A点的运动路径长（结果保留）．
19. 2022年10月16日至10月22日，中国共产党的第二十次全国代表大会在北京召开．在党的二十大召开之际，为激励引领全校青少年传承红色基因，争做党的事业接班人，某校团委组织了“红心永向党喜迎二十大”为主题的演讲比赛，根据参赛同学的得分情况绘制了如图所示的两幅不完整的统计图．（其中表示“一等奖”，表示“二等奖”，表示“三等奖”，表示“优秀奖”）
请你根据统计图中所提供的信息解答下列问题：
（1）获奖总人数为______人，______；
（2）学校将从获得一等奖的4名同学（1名男生，3名女生）中随机抽取2名参加全市的比赛，请利用树状图或列表求抽取同学中恰有1名男生和1名女生的概率．
20. 已知关于的方程
（1）取什么值时，方程有两个实数根；
（2）如果方程有两个实数根，，且，求的值．
21. 已知：如图，及外一点．请你按照步骤完成以下作图（尺规作图，保留作图痕迹）连接，以为圆心，长为半径作大圆；交小圆于点，过点作小圆切线交大圆于，两点（点在点的上方）；连接交小圆于，连接．
（1）请证明是小圆的切线；
（2）延长交大圆于，连接，若，，求的长．
22. 如图，现打算用的篱笆围成一个“日”字形菜园（含隔离栏），菜园的一面靠墙（篱笆的宽度忽略不计）
（1）菜园面积可能为吗？若可能，求边长长，若不可能，请说明理由；
（2）因场地限制，菜园的宽度不能超过，求该菜园面积的最大值．
23. 已知，如图，为的直径，弧弧．，延长交于点D
（1）求证：点P是的内心；
（2）已知的直径是，．求的长．
24. 将绕点A逆时针旋转得到，且点D落在的延长线上，连接．
（1）如图1，若，
①求的度数；
②直接写出的值．
（2）如图2，若点M，N分别为和的中点，连接并延长交于点G，求证：．
25. 已知抛物线与x轴交于A，B两点（点A在点B左侧），与y轴交于点C，点O为坐标原点．
（1）求A，B两点的坐标；
（2）若点D是线段上靠近点O的一个三等分点，点P是抛物线的一个动点，过点P作x轴的垂线，分别交、于点M，N．
①求直线的解析式（用含a的式子表示）；
摸球的次数n
1000
2000
4000
5000
8000
10000
…
摸到白球的次数m
749
1499
298
3751
6000
7501
…
摸到白球的频率
0.7490
0.7495
0.7495
0.7502
0.750
0.7501
…