人教版数学八上期末训练专题02 全等三角形突破核心考点【知识梳理+解题方法+专题过关】（2份，原卷版+解析版）

这是一份人教版数学八上期末训练专题02 全等三角形突破核心考点【知识梳理+解题方法+专题过关】（2份，原卷版+解析版），文件包含人教版数学八上期末训练专题02全等三角形突破核心考点知识梳理+解题方法+专题过关原卷版doc、人教版数学八上期末训练专题02全等三角形突破核心考点知识梳理+解题方法+专题过关解析版doc等2份试卷配套教学资源，其中试卷共66页， 欢迎下载使用。
考点一 全等图形的识别 考点二 全等三角形的性质
考点三 添加一个条件使三角形全等 考点四 全等三角形的判定
考点五 全等三角形判定的一线三等角模型 考点六 全等三角形判定的三垂直模型
考点七 全等三角形判定的倍长中线模型 考点八 全等三角形的动态问题
考点九 角的平分线的性质
【知识梳理+解题方法】
一、全等图形
概念：形状、大小相同的图形放在一起能够完全重合.
全等图形特征：①形状相同.②大小相等.③对应边相等、对应角相等.
小结：一个图形经过平移,翻折,旋转后,位置变化了,但大小和形状都没有改变,即平移,翻折,旋转前后的图形全等.
二、全等三角形
概念：两个能完全重合的三角形叫做全等三角形.
记作: ∆ABC ≌ ∆A’B’C’读作：∆ABC全等于∆A’B’C’
对应顶点：A和A’、B和B’、C和C’
对应边：AB和A’B’、BC和B’C’、AC和A’C’
对应角：∠A和∠A’、∠B和∠B’、∠C和∠C’
对应元素的规律:
(1)有公共边的，公共边是对应边；(2)有公共角的，公共角是对应角；(3)有对顶角的，对顶角是对应角；
三、 全等三角形的判定（重点）
备注：
1.判定两个三角形全等必须有一组边对应相等.2.全等三角形周长、面积相等.
四、证题的思路（难点）
五、 角平分线
概念：从一个角的顶点引出一条射线，把这个角分成完全相同的角，这条射线叫做这个角的角平分线。
角平分线的性质：角平分线上的点到角两边的距离相等；
数学语言：
∵∠MOP=∠NOP，PA⊥OM PB⊥ON
∴PA=PB
判定定理：到角两边距离相等的点在角的平分线上．
数学语言：
∵PA⊥OM PB⊥ON PA=PB
∴∠MOP=∠NOP
六、角平分线常考四种辅助线：
1.图中有角平分线，可向两边作垂线. 2.角平分线加垂线，三线合一试试看.
3.角平分线平行线，等腰三角形来添. 4.也可将图对折看，对称以后关系出现.
【专题过关+能力提升】
考点一 全等图形的识别
例题：（2021·吉林·大安市乐胜乡中学校八年级阶段练习）下列四个选项中，不是全等图形的是（ ）
A．B．C．D．
【变式训练】
1．（2022·陕西·西安市东元中学七年级阶段练习）下列四组图形中，是全等图形的一组是（ ）
A．B．C．D．
2．（2022·全国·八年级专题练习）下列各组中的两个图形属于全等图形的是（ ）
A．B．
C．D．
3．（2022·辽宁沈阳·七年级期末）对于两个图形，下列结论：①两个图形的周长相等；②两个图形的面积相等；③能够完全重合的两个图形．其中能得出这两个图形全等的结论共有（ ）
A．0个B．1个C．2个D．3个
考点二 全等三角形的性质
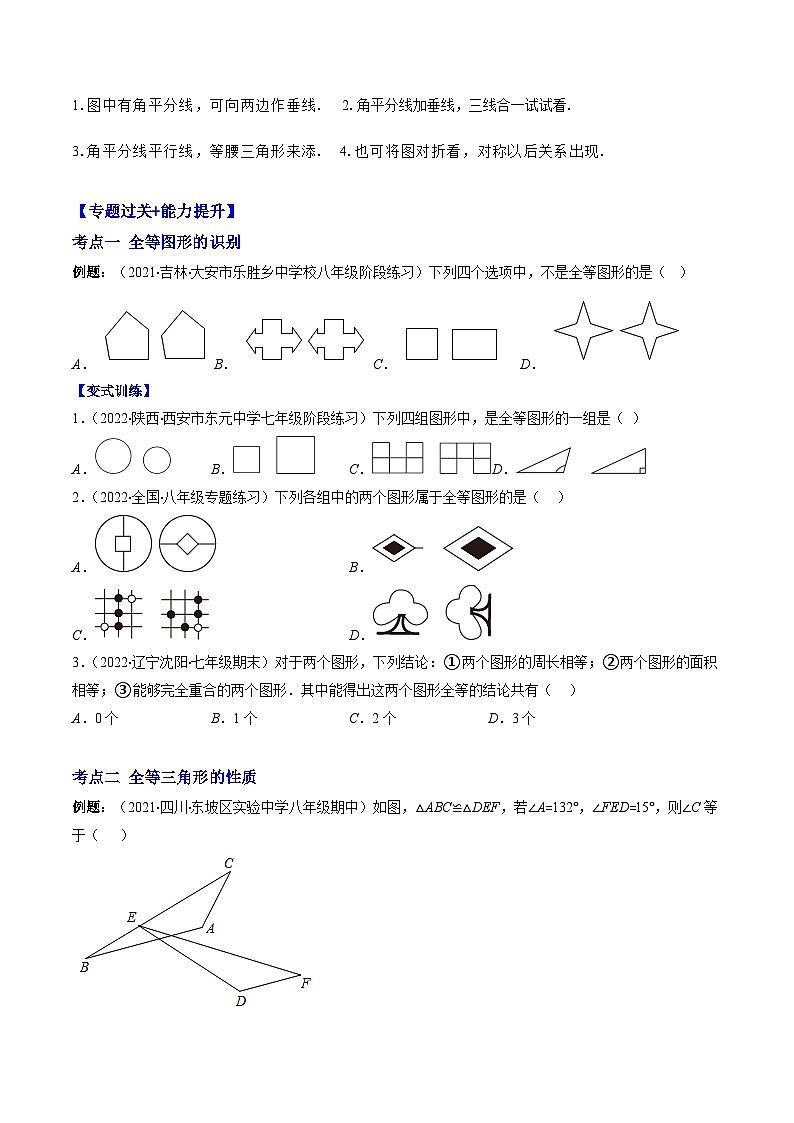
例题：（2021·四川·东坡区实验中学八年级期中）如图，△ABC≌△DEF，若∠A=132°，∠FED=15°，则∠C等于（ ）
A．13°B．23°C．33°D．43°
【变式训练】
1．（2022·贵州·贵阳市乌当区第三中学八年级期中）如图，△ABC≌△AEF，则对于结论：①AC＝AF；②∠FAB＝∠EAB；③EF＝BC；④∠EAB＝∠FAC，其中正确结论的个数是（ ）
A．1个B．2个C．3个D．4个
2．（2022·吉林省实验中学八年级阶段练习）下列结论中正确的有（ ）
①全等三角形对应边相等；②全等三角形对应角相等；③全等三角形对应中线、对应高线、对应角平分线相等；④全等三角形周长相等；⑤全等三角形面积相等．
A．5个B．4个C．3个D．2个
3．（2022·江苏·姜堰区实验初中八年级）已知△ABC≌△DEF，AB＝3，AC＝4，△DEF的周长为10，则BC的值为______．
4．（2022·江西赣州·八年级期中）如图，△ABC≌△ADE，∠B＝96°，∠BAC＝24°，那么∠AED＝______．
考点三 添加一个条件使三角形全等
例题：（2022·山东·济南市天桥区泺口实验学校七年级期中）如图，∠1=∠2，要使△ABE≌△ACE，还需要添加一个条件是_______．（写出一个即可）
【变式训练】
1．（2022·广东·深圳市布心中学七年级期末）如图，已知AC=DB，再添加一个适当的条件______，使△ABC≌△BAD．（只需填写满足要求的一个条件即可）
2．（2020·北京·垂杨柳中学八年级期中）如图，AB＝DE，∠A＝∠D＝90°，那么要得到△ABC≌△DEF，可以添加一个条件是________，△ABC与△DEF全等的理由是________．
3．（2022·浙江·金华市第五中学八年级期末）如图，点D、E分别在线段AB，AC上，AE＝AD，不添加新的线段和字母，要使△ABE和△ACD全等判定依据是AAS，需添加的一个条件是 _____．
4．（2022·湖南·新田县云梯学校八年级阶段练习）如图，AC＝AD，∠1＝∠2，只添加一个条件使△ABC≌△AED，你添加的条件是 _____．
5．（2022·河南平顶山·七年级期末）如图，已知∠1＝∠2，AC＝AE，不添加任何辅助线，再添加一个合适的条件：______，使△ABC≌△ADE．（只写出一种即可）
考点四 全等三角形的判定
例题：（2021·江西·鹰潭市余江区正源学校七年级阶段练习）如图，点B，F，C，E四点在同一条直线上，∠B＝∠E，AB＝DE，BF＝CE．求证：△ABC≌△DEF．
【变式训练】
1．（2022·江苏·泰州市姜堰区南苑学校八年级）如图， A、E、F、C在一条直线上， AF＝CE，过E、F分别作DE⊥AC，BF⊥AC，AB＝CD，求证：
(1)△ABF≌△CDE
(2)BG＝DG
2．（2020·北京二中八年级期中）如图，点B，F，C，E在直线l上（F，C之间不能直接测量），点A，D在l异侧，测得AB=DE，ABDE，∠A=∠D．
(1)求证：△ABC≌△DEF；
(2)若BE=10m，BF=3m，则FC的长度为 m．
3．（2021·吉林·大安市乐胜乡中学校八年级阶段练习）如图，△ABC的边AC与△CDE的边CE在一条直线上，且点C为AE的中点，AB =CD，BC = DE．
(1)求证：△ABC≌△CDE；
(2)将△ABC沿射线AC方向平移得到△ ，边与边CD的交点为F ，连接EF，若EF将CDE分为面积相等的两部分，且AB = 4，则 CF =
考点五 全等三角形判定的一线三等角模型
例题：（2022·全国·八年级专题练习）如图，在中，，点D在线段BC上运动（D不与B、C重合），连接AD，作，DE交线段AC于E．
(1)点D从B向C运动时，逐渐变__________（填“大”或“小”），但与的度数和始终是__________度．
(2)当DC的长度是多少时，，并说明理由．
【变式训练】
1．（2022·全国·八年级）如图，在△ABC中，点D是边BC上一点，CD＝AB，点E在边AC上，且AD＝DE，∠BAD＝∠CDE．
(1)如图1，求证：BD＝CE；
(2)如图2，若DE平分∠ADC，在不添加辅助线的情况下，请直接写出图中所有与∠ADE相等的角（∠ADE除外）．
2．（2022·全国·八年级）（1）如图①，点B、C在∠MAN的边AM、AN上，点E，F在∠MAN内部的射线AD上，∠1、∠2分别是△ABE、△CAF的外角．已知AB＝AC，∠1＝∠2＝∠BAC．求证：△ABE≌△CAF．
（2）应用：如图②，在△ABC中，AB＝AC，AB＞BC，点D在边BC上，且CD＝2BD，点E，F在线段AD上．∠1＝∠2＝∠BAC，若△ABC的面积为15，求△ABE与△CDF的面积之和．
3．（2022·河南郑州·七年级期末）在直线上依次取互不重合的三个点，在直线上方有，且满足．
(1)如图1，当时，猜想线段之间的数量关系是____________；
(2)如图2，当时，问题（1）中结论是否仍然成立？如成立，请你给出证明；若不成立，请说明理由；
(3)应用：如图3，在中，是钝角，，，直线与的延长线交于点，若，的面积是12，求与的面积之和．
考点六 全等三角形判定的三垂直模型
例题：（2021·福建·武夷山市第二中学八年级期中）如图，在△ABC中，∠ACB = 90°，AC = BC，BE ⊥CE于点E，AD ⊥CE于点D．
（1）求证：△BCE ≌△CAD；
（2）若AD =12， BE =5，求ED的长．
【变式训练】
1．（2021·天津·八年级期中）在△BAC中，∠BAC＝90°，AB＝AC，AE是过A的一条直线，BD⊥AE于点D，CE⊥AE于E．
(1)如图（1）所示，若B，C在AE的异侧，易得BD与DE，CE的关系是DE＝ ；
(2)若直线AE绕点A旋转到图（2）位置时，（BD＜CE），其余条件不变，问BD与DE，CE的关系如何？请予以证明；
(3)若直线AE绕点A旋转，（BD＞CE），问BD与DE，CE的关系如何？请直接写出结果，不需证明．
2．（2022·广东佛山·七年级阶段练习）在△ABC中，∠BAC=90°，AC=AB，直线MN经过点A，且CD⊥MN于D，BE⊥MN于E．
(1)当直线MN绕点A旋转到图1的位置时， 度；
(2)求证：DE=CD+BE；
(3)当直线MN绕点A旋转到图2的位置时，试问DE、CD、BE具有怎样的等量关系？请写出这个等量关系，并加以证明．
3．（2022·广东·河源广赋创新学校八年级阶段练习）如图，在中，，，直线经过点，且于，于．
(1)当直线绕点旋转到①的位置时，求证：①≌；②；
(2)当直线绕点旋转到②的位置时，求证：；
(3)当直线绕点旋转到③的位置时，试问、、具有怎样的数量关系？请直接写出这个等量关系，不需要证明．
4．（2021·北京·东北师范大学附属中学朝阳学校八年级期中）如图，在△ABC中，∠ACB＝90°，AC＝BC，直线l经过顶点C，过A、B两点分别作l的垂线AE、BF，E、F为垂足．
（1）当直线l不与底边AB相交时，
①求证：∠EAC＝∠BCF．
②猜想EF、AE、BF的数量关系并证明．
（2）将直线l绕点C顺时针旋转，使l与底边AB交于点D（D不与AB点重合），请你探究直线l，EF、AE、BF之间的关系．（直接写出）
考点七 全等三角形判定的倍长中线模型
例题：（2021·甘肃·庄浪县阳川中学八年级期中）已知△ABC中，AB=3，AC=4，则中线AD的取值范围是______．
【变式训练】
1．（2022·广东·深圳市龙岗区丰丽学校七年级期末）（1）如图，在中，，，点G是的中点，求中线的取值范围；
（2）如图，在四边形中，，点E是的中点．若是的平分线．试探究，，之间的等量关系，并证明你的结论．
2．（2022·山东德州·八年级期末）（1）方法呈现：
如图①：在中，若，，点D为BC边的中点，求BC边上的中线AD的取值范围．
解决此问题可以用如下方法：延长AD到点E使，再连接BE，可证，从而把AB、AC，集中在中，利用三角形三边的关系即可判断中线AD的取值范围是_______________，这种解决问题的方法我们称为倍长中线法；
（2）探究应用：
如图②，在中，点D是BC的中点，于点D，DE交AB于点E，DF交AC于点F，连接EF，判断与EF的大小关系并证明；
（3）问题拓展：
如图③，在四边形ABCD中，，AF与DC的延长线交于点F、点E是BC的中点，若AE是的角平分线．试探究线段AB，AF，CF之间的数量关系，并加以证明．
3．（2022·江苏镇江·八年级阶段练习）我们规定：有两组边相等，且它们所夹的角互补的两个三角形叫兄弟三角形．如图，OA＝OB，OC＝OD，∠AOB＝∠COD＝90°，回答下列问题：
(1)求证：△OAC和△OBD是兄弟三角形．
(2)“取BD的中点P，连接OP，试说明AC＝2OP．”聪明的小王同学根据所要求的结论，想起了老师上课讲的“中线倍长”的辅助线构造方法，解决了这个问题，按照这个思路回答下列问题．
①请在图中通过作辅助线构造△BPE≌△DPO，并证明BE＝OD；
②求证：AC＝2OP．
考点六 全等三角形的动态问题
例题：（2021·四川·东坡区实验中学八年级期中）如图，在∆ABC中，∠ACB=90°，AC=6cm，BC =8cm，点P从A点出发，沿A→C路径向终点C运动；点Q从点B出发，沿B→C→A路径向终点A运动．点P和Q分别以每秒1cm和3cm的运动速度同时开始运动．其中一点到达终点时另一点也停止运动，在某时刻，分别过点P和Q作PE⊥l于点E，QF⊥l于点F，则点P运动时间为_____时，∆PEC与∆QFC全等．
【变式训练】
1．（2021·贵州·兴义市万峰林民族学校八年级期中）如图，在长方形ABCD中，AB=6cm，BC=8cm．动点P从点B出发，沿BC方向以2cm/s的速度向点C匀速运动；同时动点Q从点C出发，沿CD方向以2cm/s的速度向点D匀速运动，当一个点停止运动时，另一个点也停止运动．设运动时间为t（s）（0