人教版数学八上期末训练专题01 三角形（突破核心考点）【知识梳理+解题方法+专题过关】（2份，原卷版+解析版）

这是一份人教版数学八上期末训练专题01 三角形（突破核心考点）【知识梳理+解题方法+专题过关】（2份，原卷版+解析版），文件包含人教版数学八上期末训练专题01三角形突破核心考点知识梳理+解题方法+专题过关原卷版doc、人教版数学八上期末训练专题01三角形突破核心考点知识梳理+解题方法+专题过关解析版doc等2份试卷配套教学资源，其中试卷共37页， 欢迎下载使用。
考点一 三角形三边关系 考点二 三角形的稳定性
考点三 三角形中的高线、中线、角平分线 考点四 三角形的内角、外角
考点五 多边形的对角线、内角和
【知识梳理+解题方法】
一、三角形的定义
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形．
要点诠释：
（1）三角形的基本元素：
①三角形的边：即组成三角形的线段；
②三角形的角：即相邻两边所组成的角叫做三角形的内角，简称三角形的角；
③三角形的顶点：即相邻两边的公共端点.
（2）三角形的定义中的三个要求：“不在同一条直线上”、“三条线段”、“首尾顺次相接”.
（3）三角形的表示：三角形用符号“△”表示，顶点为A、B、C的三角形记作“△ABC”，读作“三角形ABC”，注意单独的△没有意义；△ABC的三边可以用大写字母AB、BC、AC来表示，也可以用小写字母a、b、c来表示，边BC用a表示，边AC、AB分别用b、c表示．
二、三角形的三边关系
定理：三角形任意两边之和大于第三边.
推论：三角形任意两边的之差小于第三边.
要点诠释：
（1）理论依据：两点之间线段最短.
（2）三边关系的应用：判断三条线段能否组成三角形，若两条较短的线段长之和大于最长线段的长，则这三条线段可以组成三角形；反之，则不能组成三角形．当已知三角形两边长，可求第三边长的取值范围．
（3）证明线段之间的不等关系．
三、三角形的分类
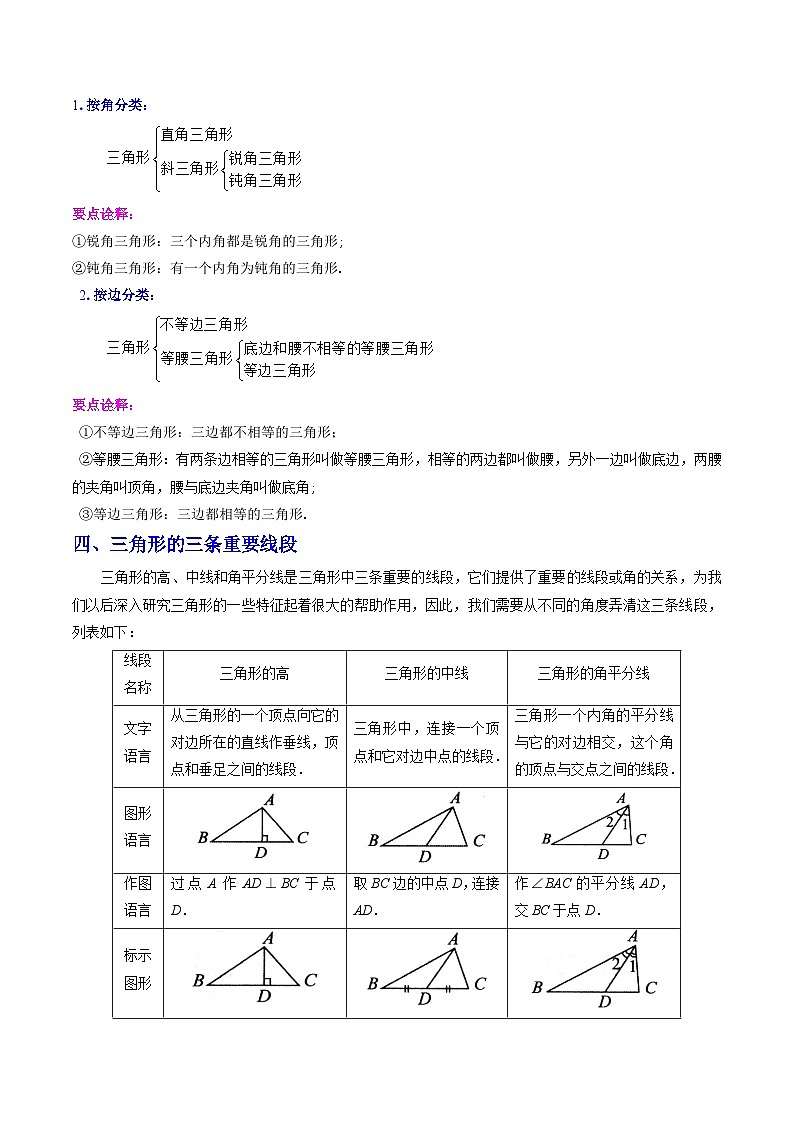
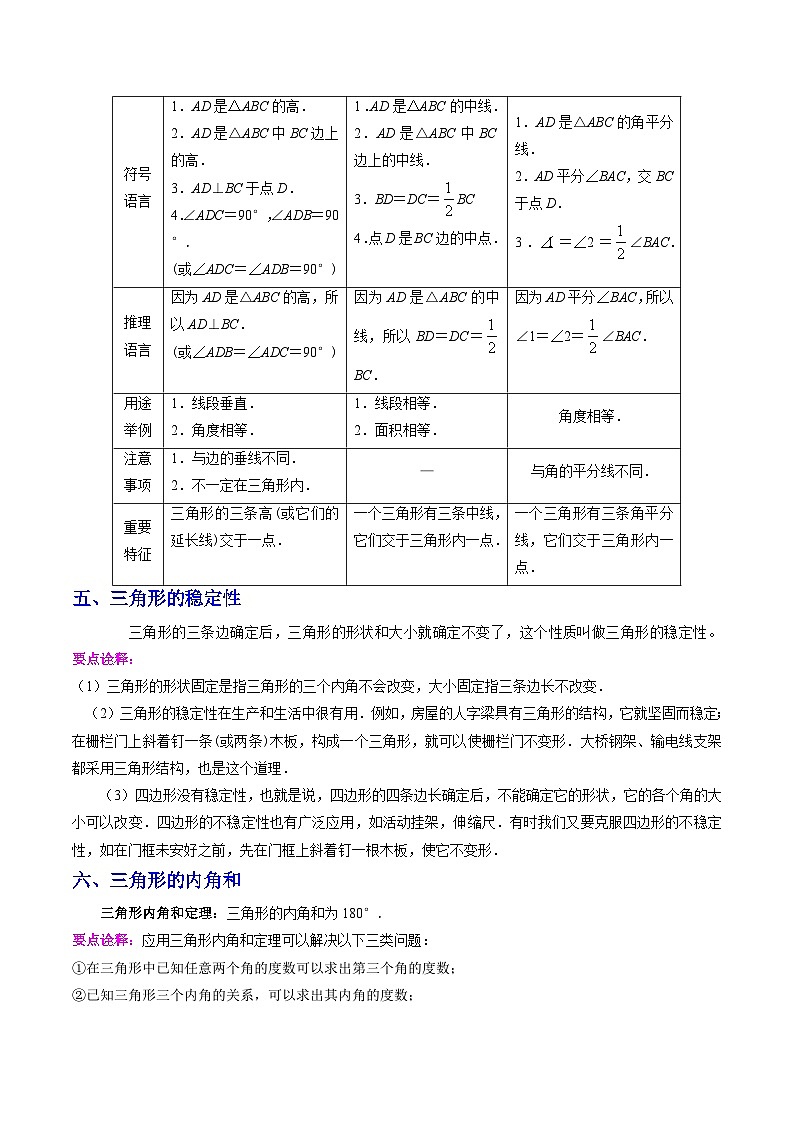
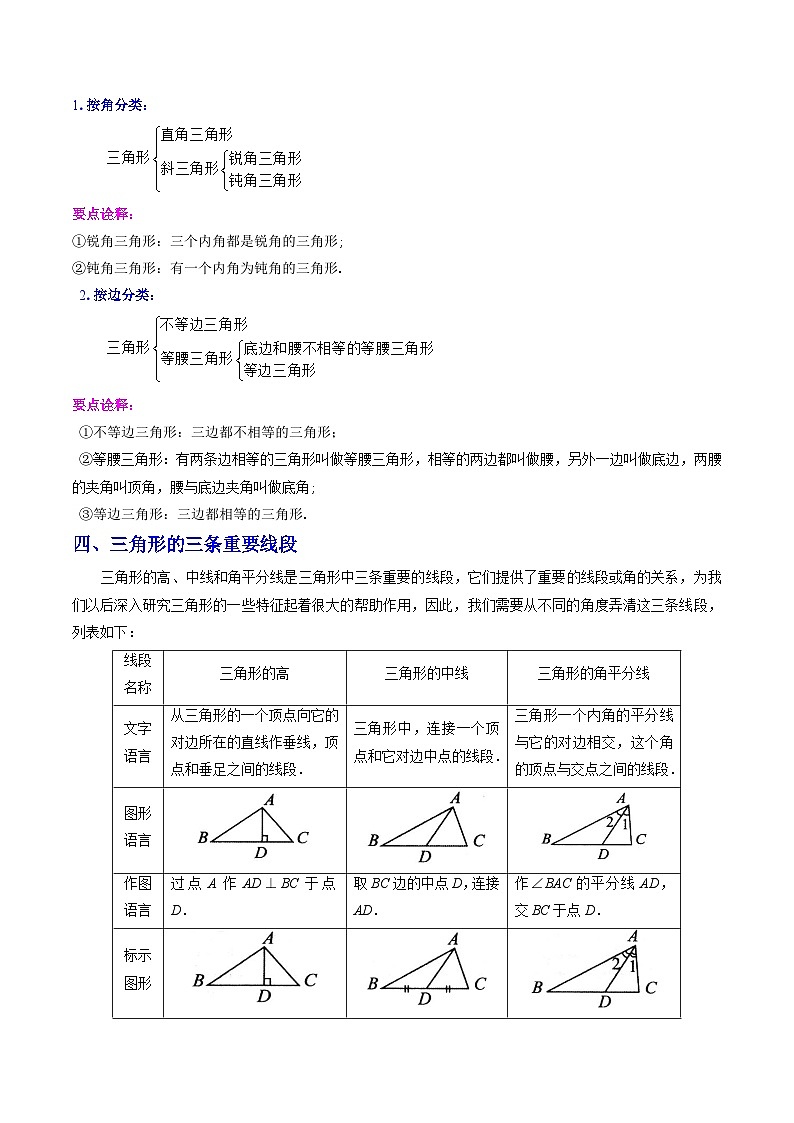
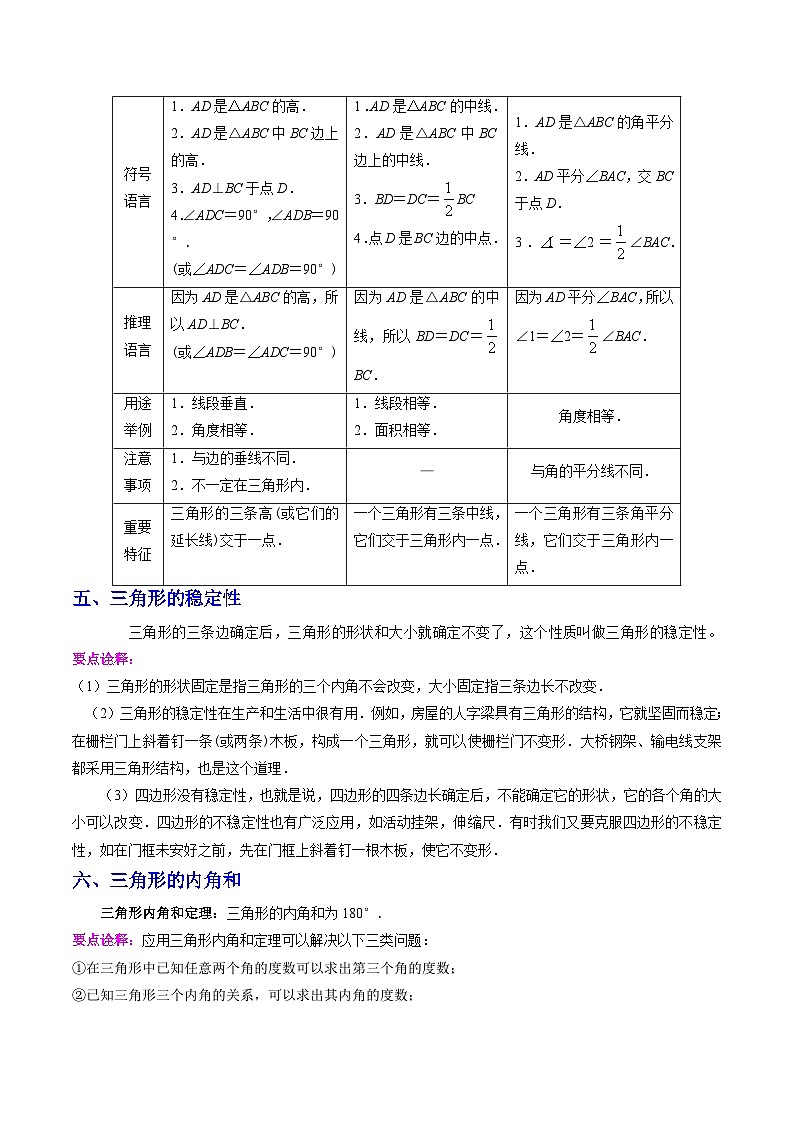
1.按角分类：
要点诠释：
①锐角三角形：三个内角都是锐角的三角形;
②钝角三角形：有一个内角为钝角的三角形.
2.按边分类：
要点诠释：
①不等边三角形：三边都不相等的三角形；
②等腰三角形：有两条边相等的三角形叫做等腰三角形，相等的两边都叫做腰，另外一边叫做底边，两腰的夹角叫顶角，腰与底边夹角叫做底角;
③等边三角形：三边都相等的三角形.
四、三角形的三条重要线段
三角形的高、中线和角平分线是三角形中三条重要的线段，它们提供了重要的线段或角的关系，为我们以后深入研究三角形的一些特征起着很大的帮助作用，因此，我们需要从不同的角度弄清这三条线段，列表如下：
五、三角形的稳定性
三角形的三条边确定后，三角形的形状和大小就确定不变了，这个性质叫做三角形的稳定性。 要点诠释：
（1）三角形的形状固定是指三角形的三个内角不会改变，大小固定指三条边长不改变．
（2）三角形的稳定性在生产和生活中很有用．例如，房屋的人字梁具有三角形的结构，它就坚固而稳定；在栅栏门上斜着钉一条(或两条)木板，构成一个三角形，就可以使栅栏门不变形．大桥钢架、输电线支架都采用三角形结构，也是这个道理．
（3）四边形没有稳定性，也就是说，四边形的四条边长确定后，不能确定它的形状，它的各个角的大小可以改变．四边形的不稳定性也有广泛应用，如活动挂架，伸缩尺．有时我们又要克服四边形的不稳定性，如在门框未安好之前，先在门框上斜着钉一根木板，使它不变形．
六、三角形的内角和
三角形内角和定理：三角形的内角和为180°．
要点诠释：应用三角形内角和定理可以解决以下三类问题：
①在三角形中已知任意两个角的度数可以求出第三个角的度数；
②已知三角形三个内角的关系，可以求出其内角的度数；
③求一个三角形中各角之间的关系．
七、三角形的外角
1．定义：三角形的一边与另一边的延长线组成的角叫做三角形的外角．如图，∠ACD是△ABC的一个外角.
要点诠释：
(1)外角的特征：①顶点在三角形的一个顶点上； ②一条边是三角形的一边；③另一条边是三角形某条边的延长线．
（2）三角形每个顶点处有两个外角，它们是对顶角．所以三角形共有六个外角，通常每个顶点处取一个外角，因此，我们常说三角形有三个外角．
2．性质：
（1）三角形的一个外角等于与它不相邻的两个内角的和．
（2）三角形的一个外角大于任意一个与它不相邻的内角．
要点诠释：三角形内角和定理和三角形外角的性质是求角度及与角有关的推理论证明经常使用的理论依据．另外，在证角的不等关系时也常想到外角的性质．
3.三角形的外角和：
三角形的外角和等于360°.
要点诠释：因为三角形的每个外角与它相邻的内角是邻补角，由三角形的内角和是180°，可推出三角形的三个外角和是360°．
八、多边形的概念
1．定义：在平面内不在同一直线上的一些线段首尾顺次相接所组成的封闭图形叫做多边形．其中，各个角相等、各条边相等的多边形叫做正多边形．
2．相关概念：
边：组成多边形的各条线段叫做多边形的边．
顶点：每相邻两条边的公共端点叫做多边形的顶点．
内角：多边形相邻两边组成的角叫多边形的内角，一个n边形有n个内角.
外角：多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
对角线：连接多边形不相邻的两个顶点的线段，叫做多边形的对角线．
凸多边形
凹多边形
3. 多边形的分类:画出多边形的任何一边所在的直线，如果整个多边形都在这条直线的同一侧，那么这个多边形就是凸多边形，如果整个多边形不在直线的同一侧，这个多边形叫凹多边形．如图：





要点诠释：
(1)正多边形必须同时满足“各边相等”，“各角相等”两个条件，二者缺一不可；
(2)过n边形的一个顶点可以引(n-3)条对角线，n边形对角线的条数为；
(3)过n边形的一个顶点的对角线可以把n边形分成(n-2)个三角形．
九、多边形内角和
n边形的内角和为(n-2)·180°(n≥3)．
要点诠释：
(1)内角和公式的应用：①已知多边形的边数，求其内角和；②已知多边形内角和求其边数；(2)正多边形的每个内角都相等，都等于；
十、多边形的外角和
多边形的外角和为360°．
要点诠释：
(1)在一个多边形的每个顶点处各取一个外角，这些外角的和叫做多边形的外角和．n边形的外角和恒等于360°，它与边数的多少无关；
(2)正n边形的每个内角都相等，所以它的每个外角都相等，都等于；
(3)多边形的外角和为360°的作用是：①已知各相等外角度数求多边形边数；②已知多边形边数求各相等外角的度数．
【专题过关+能力提升】
考点一 三角形三边关系
例题：（2022·陕西咸阳·七年级期末）一个三角形的两条边长为2，7，则第三边长可能为______（写出一个即可）
【答案】8（答案不唯一）
【分析】根据三角形的三边关系，可求出第三边的取值范围，写出一个即可．
【详解】解：设：第三条边长为a，
∴，即，
故答案为：8（答案不唯一）．
【点睛】本题考查了三角形的三边关系，求出第三边的取值范围是解答本题的关键．三角形中，两边之和大于第三边，两边之差小于第三边．
【变式训练】
1．（2022·全国·八年级专题练习）木工师傅有两根长分别为80cm、150cm的木条，要再找一根木条，将它们钉成一个三角形框架，现有70cm、200cm、300cm三根木条，他可选择长为______的木条．
【答案】200cm
【分析】设第三边长为xcm，再根据三角形的三边关系求出x的取值范围，找出符合条件的木条即可．
【详解】设第三边长为xcm，
∵木工师傅有两根长分别为80cm、150cm的木条，
∴150−80x150+80，
即70x230，
故符合条件木条的长度应在70cm与230cm之间，
故答案为：200cm．
【点睛】本题考查了三角形的三边关系，解题的关键是掌握任意两边之和大于第三边，任意两边之差小于第三边．
2．（2022·江苏·靖江市实验学校八年级期中）已知三角形三边分别为、、，其中、满足，那么c的取值范围是______．
【答案】##
【分析】首先根据非负数的性质计算a、b的值，然后根据三角形三边的关系可得c的取值范围．
【详解】解：∵，
∴，，
∴，，
∴，
∴．
故答案为：．
【点睛】本题主要考查了非负数的性质和三角形三边关系，根据非负数的性质确定a、b的值是解题关键．
3．（2020·湖北·公安县教学研究中心八年级期中）已知三角形的三条边长为6、10和x．
(1)若6是最短边长，求x的取值范围；
(2)若x为整数，求三角形周长的最大值．
【答案】(1)6≤x＜16
(2)31
【分析】（1）根据三角形的三边关系，即可求解；
（2）根据三角形的三边关系，可得4＜x＜16，再由x为整数，可得x的最大值为15，即可求解．
（1）
解：由题意得：10－6＜x＜10＋6，即4＜x＜16
∵6是最短边长，
∴x≥6
∴x的取值范围是6≤x＜16；
（2）
解：由（1）可知，4＜x＜16，
∵x为整数，
∴x的最大值为15，
∴三角形周长的最大值为6＋10＋15＝31．
【点睛】本题主要考查了三角形的三边关系，熟练掌握三角形的两边之和大于第三边，两边之差小于第三边是解题的关键．
4．（2021·江西·鹰潭市余江区正源学校七年级阶段练习）已知三角形的两边长为8和10，第三边长x最小．
(1)求x的取值范围；
(2)当x为何值时，围成的三角形周长最大？并求出周长．
【答案】(1)2＜x≤8
(2)当x＝8时，三角形的周长最大，为26
【分析】（1）根据三角形的任意两边之和大于第三边，两边之差小于第三边求出第三条边长x的取值范围．
（2）由（1）可知，当x=8时，三角形周长最大，据此求解即可．
（1）
由三角形的三边关系，得2＜x＜18，
∵x为最小，
∴x的取值范围是2＜x≤8；
（2）
当x＝8时，三角形的周长最大，
且最大值是8+10+8＝26．
【点睛】本题考查了三角形的三边关系，熟记其性质是解题的关键．
考点二 三角形的稳定性
例题：（2022·四川·富顺第二中学校八年级阶段练习）下列生活实物中，没有应用到三角形的稳定性的是（ ）
A． B． C． D．
【答案】D
【分析】根据三角形的稳定性解答即可．
【详解】解：选项D中活动衣架上没有三角形，其余A、B、C选项中都含有三角形，
由三角形的稳定性可知，选项D中没有利用三角形的稳定性，
故选：D．
【点睛】本题考查了三角形的稳定性，正确的理解题意是解题的关键．
【变式训练】
1．（2022·全国·八年级专题练习）如图所示，一扇窗户打开后，用窗钩AB即可固定，这里所用的几何原理是（ ）
A．两点之间线段最短B．垂线段最短．
C．两定确定一条直线D．三角形具有稳定性
【答案】D
【分析】三角形具有稳定性的实际应用．
【详解】根据题意窗钩AB可固定，用的是三角形（图中的）的稳定性，
故选：D．
【点睛】本题考查了三角形的稳定性性质的实际应用，理解性质是解题关键．
2．（2021·吉林·大安市乐胜乡中学校八年级阶段练习）如图、手机支架采用了三角形结构，这样设计依据的数学道理是三角形具有____________性．
【答案】稳定
【分析】根据三角形的稳定性即可求解．
【详解】解：手机支架采用了三角形结构，这样设计依据的数学道理是三角形具有稳定性．
故答案为：稳定
【点睛】本题考查了三角形的稳定性，理解三角形具有稳定性是解题的关键．
3．（2022·黑龙江·兰西县红星乡第一中学校七年级期中）如图所示的是自行车的三角形支架，这是利用三角形具有 ________________．
【答案】稳定性
【分析】根据三角形的特性即可解答．
【详解】解：∵三角形具有稳定性，
∴自行车三角形支架是利用了三角形稳定性的特性．
故答案为：稳定性．
【点睛】本题考查了三角形的特性，解决本题的关键是掌握三角形的特性．
考点三 三角形中的高线、中线、角平分线
例题：（2022·全国·八年级专题练习）在下列各图中，正确画出△ABC的边BC上的高的是（ ）
A． B． C． D．
【答案】C
【分析】根据三角形高线的定义，即可求解．
【详解】解：由题可得，过点A作BC的垂线段，垂足为D，则AD是△ABC的边BC上的高，
所以C选项符合题意，
故选：C．
【点睛】本题主要考查了三角形高线的定义，熟练掌握从三角形的一个顶点向对边所在直线作垂线，顶点与垂足间的线段叫做三角形的高是解题的关键．
【变式训练】
1．（2021·湖北·公安县教学研究中心八年级阶段练习）如图，AD为BC边上的中线，E为AD的中点，连接BE、CE，若图中阴影部分的面积为10，则△ABC的面积为（ ）
A．5B．10C．15D．20
【答案】D
【分析】根据三角形面积公式，三角形的中线将三角形分成面积相等的两部分，则，，，进而推出即可解答．
【详解】解：∵E为AD的中点，
∴，，
∵AD为BC边上的中线，
∴，
∵，
∴，
∴；
故选：D．
【点睛】本题考查了三角形的面积以及三角形中线的性质，熟练掌握三角形的中线将三角形分成面积相等的两部分是解题的关键．
2．（2022·江苏·盐城市初级中学七年级期中）如图，，，为中线，则与的周长之差为（ ）
A．1B．2C．3D．4
【答案】C
【分析】根据三角形的周长的计算方法得到△ABD的周长和△ADC的周长的差就是AB与AC的差．
【详解】解：∵AD为中线，
∴BD＝CD，
又，，
∴
＝（AB＋AD＋BD）−（AC＋AD＋CD）
＝AB＋AD＋BD−AC−AD−CD
＝AB−AC
＝8−5
＝3，
故选：C．
【点睛】本题考查三角形的中线的定义：三角形一边的中点与此边所对顶点的连线叫做三角形的中线，同时考查了三角形周长的计算方法．
3．（2021·吉林·大安市乐胜乡中学校八年级阶段练习）如图，CM是△ABC的中线，若AC= 8，BC= 11，则△BCM与△ACM的周长的差是__________
【答案】3
【分析】利用中线的性质，进行计算即可．
【详解】解：∵CM是△ABC的中线，
∴，
则：，
即，
故答案为：3．
【点睛】本题考查三角形中线的性质，合理利用中线得到线段的中点平分线段是解题的关键．
4．（2022·广东·佛山市顺德区华南师范大学附属北滘学校七年级期中）如图，在△ABC中，D、E分别为边BC，AC的中点，，则其中阴影部分的面积是_____．
【答案】12
【分析】先根据三角形中线的定义可得，再根据三角形的面积公式即可得．
【详解】解：分别为边的中点，
，
，
，
又，
，
即其中阴影部分的面积是12，
故答案为：12．
【点睛】本题考查了与三角形中线有关的面积计算，熟练掌握三角形中线的性质是解题关键．
5．（2022·江苏·宜兴市和桥镇第二中学七年级期中）如图，每个小正方形的边长为1个单位，每个小方格的顶点叫格点．
(1)画出的边上的高，垂足为；
(2)求出的面积为_________；
(3)图中，能使的格点，共有_________个．
【答案】(1)画图见解析
(2)8
(3)7
【分析】（1）根据三角形高的定义作图即可；
（2）用△ABC所在的长方形面积减去周围3个三角形面积再减去一个小长方形面积即可得到答案；
（3）利用格点和平行线间间距相等作图求解即可．
（1）
解：如图所示，线段CD即为所求；
（2）
解：，
故答案为：8；
（3）
解：如图所示，满足Q点的格点一共有7个，
故答案为：7；
【点睛】本题主要考查了求三角形面积，平行线的性质，画三角形的高，熟知相关知识是解题的关键．
考点四 三角形的内角、外角
例题：（2022·上海·八年级开学考试）如图，∠DBC与∠ECB是△ABC的两个外角，BF平分∠DBC交∠ECB的平分线于点F．若∠F＝60°，则∠A＝__．
【答案】
【分析】由角平分线的定义及三角形的内角和定理可得，进而利用平角定义和三角形的内角和定理求解．
【详解】解：∵BF平分∠DBC，CF平分∠ECB，
∴∠ECB＝2∠BCF，∠DBC＝2∠CBF，
∵∠F＝60°，
∴ ，
∴ ，
∴ ，
∴ ．
故答案为： ．
【点睛】本题考查三角形外角的性质及三角形的内角和定理，解答的关键是熟练应用外角和内角的关系．
【变式训练】
1．（2022·新疆塔城·七年级期末）已知：直线，一块含角的直角三角板如图所示放置，，则等于_________．
【答案】33°##33度
【分析】先根据三角形外角的性质求出的度数，再由平行线的性质得出的度数，由直角三角形的性质及对顶角相等即可得出结论．
【详解】解：如图，
是的外角，
，
，
，
，
，
．
故答案为：．
【点睛】本题考查的是平行线的性质及三角形外角的性质，用到的知识点为：两直线平行，同位角相等．
2．（2021·吉林·大安市乐胜乡中学校八年级阶段练习）如图，在△ABC中，AD平分∠BAC交BC于点D，BE平分Z．ABC交AD于点E．
(1)若∠C= 60°，∠BAC = 80°，求∠ADB的度数；
(2)若∠BED = 60°，求∠C的度数．
【答案】(1)100°
(2)60°
【分析】（1）由角平分线的定义可得∠DAC＝40°，再由三角形外角性质即可求∠ADB的度数；
（2）由三角形的外角性质可得∠BAD＋∠ABE＝60°，再由角平分线的定义得∠BAC＝2∠BAD，∠ABC＝2∠ABE，从而得∠BAC＋∠ABC＝120°，利用三角形的内角和即可求∠C的度数；
（1）
∵AD平分∠BAC,∠BAC=80°
∴．
∵是的外角，
∴；
（2）
∵是的外角，，
∴．
∵，分别是，的角平分线，
∴，，
∴．
∵，
∴；
【点睛】本题主要考查三角形的内角和定理以及外角的性质，解答的关键是结合图形分析清楚各角之间的关系．
3．（2022·新疆乌鲁木齐·八年级阶段练习）如图，在△ABC中，BD是AC边上的高，∠A＝70°
(1)求∠ABD；
(2)CE平分∠ACB交BD于点E，∠BEC＝118°，求∠ABC．
【答案】(1)20°
(2)54°
【分析】（1）根据高的定义求得为直角，结合即可求出的度数；
（2）首先根据外角的性质求出的度数，再结合角平分线的定义求出的度数，进而求出的度数．
（1）
解：在中，
是边上的高，
，
，
；
（2）
解：在中，
，且，，
，
平分，
，
，
．
【点睛】本题主要考查了三角形内角和定理，解题的关键是掌握三角形的内角和为，此题难度不大．
4．（2022·江苏·扬州中学教育集团树人学校七年级阶段练习）已知点A在射线CE上，∠BDA＝∠C．
(1)如图1，若，求证：；
(2)如图2，若∠BAC＝∠BAD，BD⊥BC，请证明∠DAE+2∠C＝90°；
【答案】(1)见解析
(2)见解析
【分析】（1）根据两直线平行，内错角相等，得到∠DAE＝∠BDA，再根据∠BDA＝∠C得到∠DAE＝∠C，即可得到结果；
（2）根据三角形的外角等于其余两内角之和可得到∠BGA＝∠BDA+DAE，根据三角形内角和为得到∠BGA+∠C＝90°，再根据∠DAE＝∠C，可得到结果．
（1）
证明：∵ACBD，
∴∠DAE＝∠BDA，
∵∠BDA＝∠C，
∴∠DAE＝∠C，
∴ADBC；
（2）
证明：如图2，设CE与BD相交于点G，∠BGA＝∠BDA+DAE，
∵BD⊥BC，
∴∠BGA+∠C＝90°，
∴∠BDA+∠DAE+∠C＝90°，
∵∠BDA＝∠C，
∴∠DAE+2∠C＝90°．
【点睛】本题考查了两直线平行内错角相等，三角形外角等于其余两内角之和，三角形内角和为，解题的关键是找到角之间的关系．
5．（2022·广东·东莞市松山湖莞美学校八年级阶段练习）如图，AD为△ABC的中线，BE为三角形ABD中线；
(1)若∠ABE＝15°，∠BAD＝35°，求∠BED的度数；
(2)若AE＝5cm，AB＝16cm，AC＝14cm，△ABE的周长比△BDE的周长大3cm，求△ACD的周长．
(3)若△ABC的面积为60cm2，BD＝5cm，则点E到BC边的距离为多少cm？
【答案】(1)50°
(2)37cm
(3)6
【分析】（1）根据三角形外角的性质可求解；
（2）利用三角形中线的性质及三角形的周长公式可求得CD＝BD＝13cm，进而可求解；
（3）过E点作EF⊥BC于点E，先根据三角形的中线把三角形分成面积相等的两个小三角形，结合题意可求得△BED的面积，再直接求点E到BC边的距离即可．
（1）
解：∵∠BED是△ABE的一个外角，∠ABE＝15°，∠BAD＝35°，
∴∠BED＝∠BAD+∠ABE＝35°+15°＝50°；
（2）
解：∵AD为△ABC的中线，BE为△ABD的中线，AE＝5cm，
∴BD＝CD，AD＝2AE＝10cm，
∵△ABE的周长比△BDE的周长大3cm，
∴AB+BE+AE﹣（BD+BE+DE）＝3，
化简得AB﹣BD＝3（cm），
∵AB＝16cm，
∴CD＝BD＝16﹣3＝13（cm），
∵AC＝14cm，
∴△ACD的周长为：AC+CD+AD＝14+13+10＝37（cm）；
（3）
解：过E点作EF⊥BC于点E，
∵AD为△ABC的中线，BE为△ABD中线，
∴＝×60＝15；
∵BD＝5，
∴EF＝，
即点E到BC边的距离为6．
【点睛】本题主要考查了三角形的高、中线，三角形的面积和三角形的外角等知识，注意全面考虑问题，熟记三角形的中线把三角形分成的两个小三角形面积一定相等．
考点五 多边形的对角线、内角和
例题：（2022·贵州省三穗中学八年级期中）若一个多边形的内角和是900°，则这个多边形是____边形． 共________条对角线
【答案】 七 14
【分析】设这个多边形是边形，根据多边形的内角和公式，列式求得多边形的边数，再根据对角线公式求解即可．
【详解】解：设这个多边形是边形，根据题意得，
，
解得．
∴该多边形的对角线数为（条）
故答案为：七；14．
【点睛】本题主要考查了多边形的内角和公式及多边形的对角线公式，熟记公式是解题的关键．
【变式训练】
1．（2022·安徽安庆·八年级期末）一个多边形的内角和是外角和的4倍，这个多边形的对角线有 _____条．
【答案】35
【分析】一个多边形的内角和等于外角和的4倍而任何多边形的外角和是360°，因而多边形的内角和等于1440°．n边形的内角和可以表示成（n-2）•180°，设这个正多边形的边数是n,就得到方程，从而求出边数，即可求出答案．
【详解】解：设这个正多边形的边数是n,则，
解得：n=10．
则从这个多边形一个顶点可以引7条对角线，
故这个多边形共有条对角线．
故答案为：35．
【点睛】本题主要考查多边形内角与外角的知识点，此题比较简单，只要结合多边形的内角和公式寻求等量关系，构建方程求解即可．从n边形一个顶点可以引条对角线．
2．（2022·宁夏·中宁县第三中学八年级期末）一个正多边形的内角和等于1440°，则此多边形是________边形．
【答案】10##十
【分析】设这个多边形的边数为n，根据内角和公式得出（n2）×180°=1440，求出方程的解即可．
【详解】解：设这个多边形的边数为n，
则（n2）×180°=1440°，
解得：n=10，
即这个多边形是10边形，
故答案为：10．
【点睛】本题考查了多边形的内角与外角，能熟记多边形的内角和公式是解此题的关键，注意：边数为n（n≥3）的多边形的内角和=（n2）×180°．
3．（2021·湖北·公安县教学研究中心八年级阶段练习）（1）已知一个多边形是正六边形，求这个正六边形每个内角的度数；
（2）已知一个多边形的内角和与外角和相等，求这个多边形的边数．
【答案】（1）正六边形每个内角的度数为120°；（2）这个多边形的边数为4
【分析】（1）利用正六边形的内角和公式求出外角的度数即可解决问题；
（2）利用多边形的内角和与外角和公式列出方程，然后解方程即可．
【详解】（1）正六边形的内角和为(6-2)×180°=720°
正六边形每个内角的度数为720°÷6=120°
（2）设这个多边形的边数为n，根据题意得
(n-2)×180°=360°
解得n=4
即这个多边形的边数为4.
【点睛】此题主要考查了多边形内角和与外角和．解题的关键是掌握多边形内角和公式，明确外角和是360°．
4．（2022·河南信阳·七年级期末）如图，在六边形ABCDEF中，AFBECD，EDAB，∠A=110°，∠ABC=100°．
(1)求六边形ABCDEF的各内角和的度数；
(2)求∠C、∠D的度数；
(3)若一只蚂蚁从A点出发沿A-B-C-D-E-F-A运动到A点停止，蚂蚁一共转过了多少度？
【答案】(1)
(2)，
(3)
【分析】（1）根据两直线平行，同旁内角互补，得出，，，，全部相加即为六边形ABCDEF的内角和；
（2）根据平行线的性质，得出，，，，再利用角之间的换算，则可计算出答案；
（3）利用多边形的外角和为的性质即可．
（1）
∵AFBECD，
∴，，，，
∴六边形ABCDEF的各内角和
；
（2）
∵AFBECD，
∴，，，
∴，
∵EDAB，
∴，
∴，
；
（3）
由于蚂蚁从A点出发沿A-B-C-D-E-F-A运动到A点停止，
即绕了多边形一周，转过的角度多边形为外角和，
∴蚂蚁一共转过了．
【点睛】本题考查了平行线的性质，多边形外角和定理，解题关键是灵活运用平行线的性质进行角之间的换算．
5．（2022·江苏镇江·七年级期中）如图①，在△ABC中，∠ABC与∠ACB的平分线相交于点P．
(1)如果∠ABC＝50°，∠ACB＝60°，则∠BPC= °；
(2)如图②，作△ABC外角∠MBC，∠NCB的角平分线交于点Q，直接写出∠Q与∠BPC之间满足的数量关系 ；
(3)如图③，延长线段BP、QC交于点E，若∠Q=∠E，求∠A的度数．
【答案】(1)125
(2)∠Q+∠BPC=180°
(3)∠A＝72°
【分析】（1）依据∠ABC和∠ACB的平分线相交于点P，可得∠2+∠4的度数，依据三角形内角和定理，即可得到∠BPC的度数；
（2）根据角平分线的定义和平角的定义可得出，再由四边形的内角和定理可得结论；
（3）根据题意求出∠Q=54°，从而得∠QBC+∠QCB=126°，∠MBC+∠NCB=252°，∠ABC+∠ACB=108°，最后由三角形内角和定理可得结论．
（1）
如图，
∵∠ABC=50°，∠ACB=60°，∠ABC和∠ACB的平分线相交于点P，
∴∠2+∠4=25°+30°=55°，
∴△BCP中，∠P=180°-55°=125°，
故答案为：125；
（2）
∵BP平分∠ABC，
∴
∵BQ平分
∴
又
∴，
同理可得，
∵
∴
（3）
∵∠EBQ＝90°．且∠Q＝∠E，
∴∠E+∠E=90°,
∴∠E=36°，,
∴∠Q=54°
∴∠QBC+∠QCB=126°，
∴∠MBC+∠NCB=252°
∴∠ABC+∠ACB=108°，
∴∠A＝180°-（∠ABC+∠ACB）=72°．
【点睛】本题是三角形综合题，考查了三角形内角和定理、外角的性质，角平分线定义等知识；灵活运用三角形的内角和定理、外角的性质是解题的关键．
线段名称
三角形的高
三角形的中线
三角形的角平分线
文字语言
从三角形的一个顶点向它的对边所在的直线作垂线，顶点和垂足之间的线段．
三角形中，连接一个顶点和它对边中点的线段．
三角形一个内角的平分线与它的对边相交，这个角的顶点与交点之间的线段．
图形语言
作图语言
过点A作AD⊥BC于点D．
取BC边的中点D，连接AD．
作∠BAC的平分线AD，交BC于点D．
标示图形
符号语言
1．AD是△ABC的高．
2．AD是△ABC中BC边上的高．
3．AD⊥BC于点D．
4．∠ADC＝90°，∠ADB＝90°．
(或∠ADC＝∠ADB＝90°)
1．AD是△ABC的中线．
2．AD是△ABC中BC边上的中线．
3．BD＝DC＝BC
4．点D是BC边的中点．
1．AD是△ABC的角平分线．
2．AD平分∠BAC，交BC于点D．
3．∠1＝∠2＝∠BAC．
推理语言
因为AD是△ABC的高，所以AD⊥BC．
(或∠ADB＝∠ADC＝90°)
因为AD是△ABC的中线，所以BD＝DC＝BC．
因为AD平分∠BAC，所以∠1＝∠2＝∠BAC．
用途举例
1．线段垂直．
2．角度相等．
1．线段相等．
2．面积相等．
角度相等．
注意事项
1．与边的垂线不同．
2．不一定在三角形内．
—
与角的平分线不同．
重要特征
三角形的三条高(或它们的延长线)交于一点．
一个三角形有三条中线，它们交于三角形内一点．
一个三角形有三条角平分线，它们交于三角形内一点．