初中数学人教版（2024）七年级上册（2024）6.3 角完整版课件ppt

1.理解角的形成，建立几何中角的概念，掌握角的两种定义形式和四种表示方法。2.通过在图片、实例中找角，培养学生的观察、探究、抽象、概括的能力以及把实际问题转化为数学问题的能力。3.了解方位角，能确定具体物体的方位。
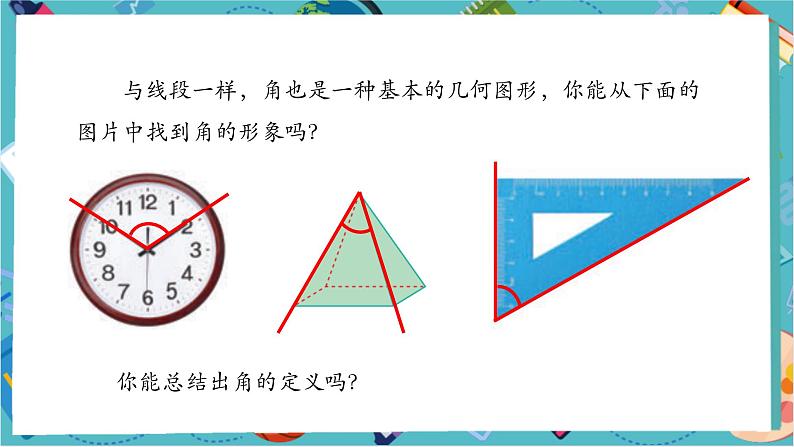
与线段一样，角也是一种基本的几何图形，你能从下面的图片中找到角的形象吗？
　　你能总结出角的定义吗？
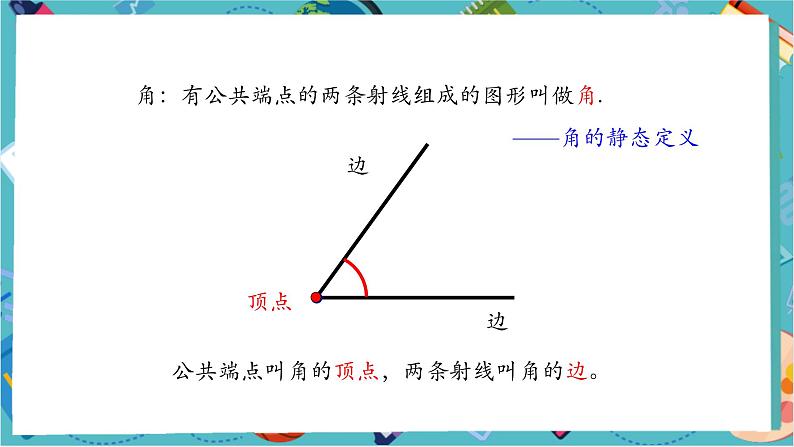
角：有公共端点的两条射线组成的图形叫做角.
公共端点叫角的顶点，两条射线叫角的边。
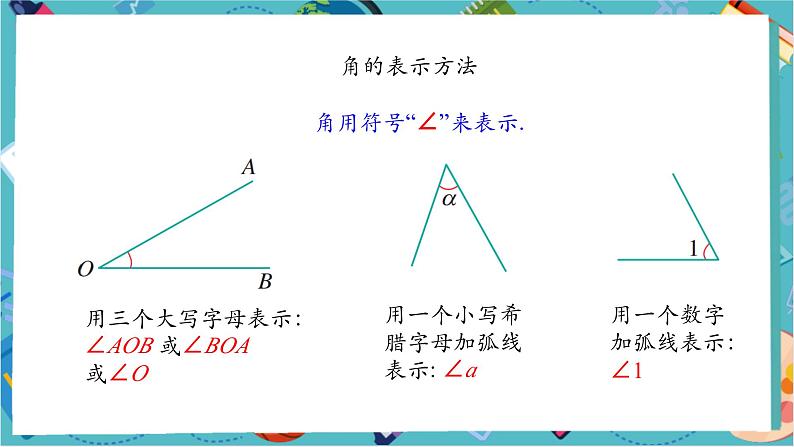
用三个大写字母表示：∠AOB 或∠BOA或∠O
用一个小写希腊字母加弧线表示: ∠a
用一个数字加弧线表示： ∠1
角用符号“∠”来表示.
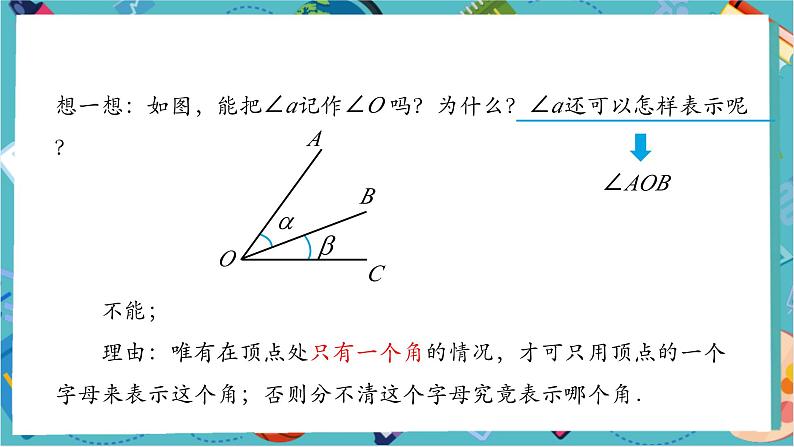
想一想：如图，能把∠a记作∠O 吗？为什么？∠a还可以怎样表示呢？
　　不能；　　理由：唯有在顶点处只有一个角的情况，才可只用顶点的一个字母来表示这个角；否则分不清这个字母究竟表示哪个角．
角：也可以看作由一条射线绕着它的端点旋转而形成的图形．——角的动态定义
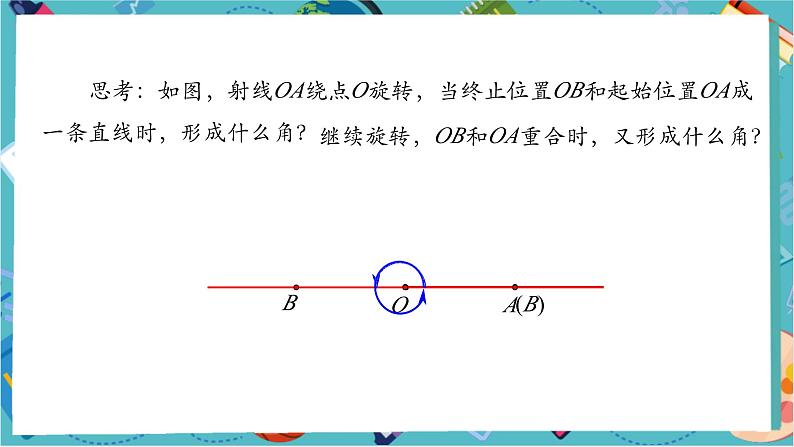
思考：如图，射线OA绕点O旋转，当终止位置OB和起始位置OA成一条直线时，形成什么角？
继续旋转，OB和OA重合时，又形成什么角？
　　平角：当射线OA绕O点旋转，当终止位置OB与起始位置OA在一条直线上时，形成平角；
　　周角：当射线OA绕O点旋转，当终止位置OB与起始位置OA重合时，形成周角．
　　仔细观察下面的动图，你有什么发现？
归 纳1．平角和周角都是“角”，而不是“线”．因此，不能说“一条直线就是平角”，也不能说“一条射线就是周角” ．2．平角的一半是直角，1直角＝90°，通常在直角的顶点处加上“ ”或“　”标志．
我们常用量角器量角. 度、分、秒是常用的角的度量单位.
角的度、分、秒是60进制的，这和计量时间的时、分、秒是一样的.
1 ′ ＝60 ′′
把一个周角360等分，每一份就是1度的角，记作1°；
把1度的角60等分，每一份叫做1分 的角，记作1′；
把１分的角60等分， 每一份叫做1秒的角， 记作1′′
想一想：借助三角尺，我们能直接画出哪些度数的特殊角？
想一想：如何借助量角器来度量角的度数呢？
用量角器度量角的方法:1．对中——角的顶点对准量角器的中心；2．重合——角的一边与量角器的零线重合；3．读数——读出角的另一边所对的度数．
借助量角器 ， 可以画出任何给定度数的角.
∠α 的度数是48度56分37秒，记作：∠α＝48°56′37 ′′
角度制：以度 、 分 、 秒为单位的角的度量制 ， 叫做角度制.
除量角器外，工程测量中，还常用经纬仪来测量角的大小
最早明确使用角度制的文字记载于希腊学者托勒密（Ptlemaeus， 约90—168）的 《天文学大成》。托勒密在书中将圆周分为360等份，将１份记为1°，并采用古巴比伦的六十进制，定义出度、分、秒，这样便形成了角度制。
例：如图，货轮O在航行过程中,发现灯塔A在它南偏东60º的方向上。同时，在它北偏东40º、南偏西10º、西北(即北偏西45º)方向上又分别发现了客轮B、货轮C和海岛D。仿照表示灯塔方位的方法，画出表示客轮B、货轮C和海岛D方向的射线。
在航行、测绘等工作中，经常以正北、正南方向为基准，描述物体运动的方向，如“北偏东30°” “南偏西25°”．
【知识技能类作业】必做题：
1.判断下面各角的表示方法是否正确.
2. 下面表示∠DEF的图是( )
3．学校里的荷花池在升旗台的南偏东25°方向200米处．下面（ ）图符合这句话的描述。 A． B． C． D．
【知识技能类作业】选做题：
4.如图，写出这四个城市相应钟表上时针与分针所成角的度数：
解：(1)30°　(2)0°　(3)120°　(4)90°
5.请你把图中用数字表示的角改为用字母表示的角．
解：∠1＝∠BAC，∠2＝∠B，∠3＝∠C，∠4＝∠DAC．
1.下列关于角的说法正确的是（　　）A．两条射线组成的图形叫做角B．延长一个角的两边C．角的两边是射线，所以角不可以度量D．角的大小与这个角的两边长短无关
2.下列图中能用∠AOB，∠O，∠1三种方法表示同一个角的图形是( )
4.将图中的角用不同的方法表示出来，并填写下表．
∠BAC（或∠BAE）