初中1.4平行线的性质教学课件ppt

这是一份初中1.4平行线的性质教学课件ppt，共20页。PPT课件主要包含了学习任务，复习回顾，猜一猜，内错角相等，同旁内角互补，知识精讲，角的相等或互补，两直线平行，∴∠1∠2，同角的补角相等等内容，欢迎下载使用。
理解并掌握平行线的性质二、三？
灵活运用平行线的性质解决问题？
两条平行线被第三条直线所截，同位角相等.
简单说成：两直线平行，同位角相等.
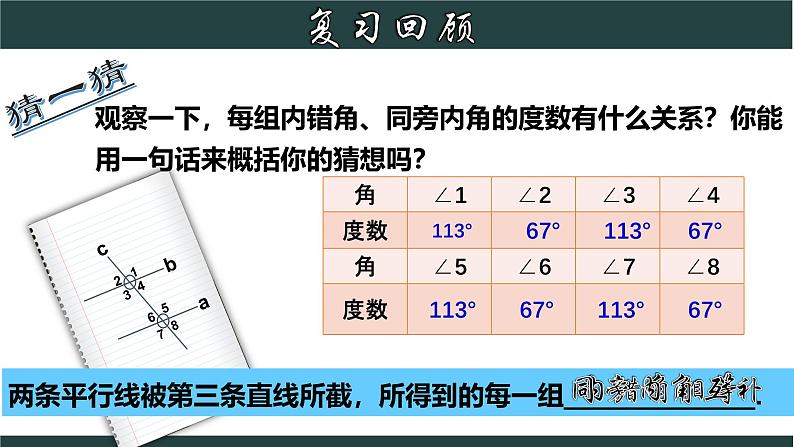
观察一下，每组内错角、同旁内角的度数有什么关系？你能用一句话来概括你的猜想吗？
两条平行线被第三条直线所截，所得到的每一组_____________.
你能用性质1来解决下面问题吗？试试看.
证明：∵ a∥ b（已知）∴∠1=∠2（两直线平行，同位角相等）又∵∠1与∠3互为对顶角（已知）∴∠1=∠3（对顶角相等）∴ ∠2=∠3（等量代换）
两条平行线被第三条直线所截，内错角相等.
简单说成：两直线平行，内错角相等.
你能用已有性质来解决下面问题吗？试试看。
证明：∵ a∥ b（已知）∴∠1=∠2（两直线平行，同位角相等）又∵∠1与∠4互为邻补角（已知）∴∠1+∠4=180°（邻补角互补）∴ ∠2+∠4=180° （等量代换）
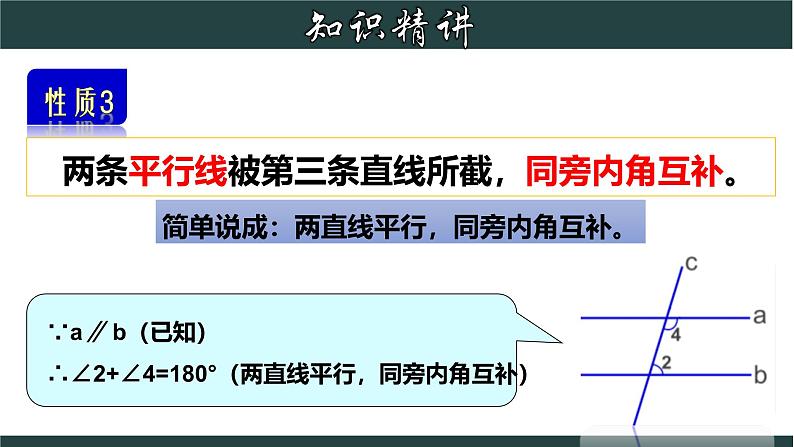
两条平行线被第三条直线所截，同旁内角互补。
简单说成：两直线平行，同旁内角互补。
2.判定是已知 推出 ；
性质是已知 ，说明 .
例3:如图,已知AB∥CD，AD∥BC.判断∠1与∠2是否相等，并说明理由.
解：∵AB∥CD（已知）
∴ ∠1+ ∠BAD=1800
（两直线平行，同旁内角互补）
∴ ∠2+ ∠BAD=1800
例4：如图,已知∠ABC+∠C=180°,BD平分∠ABC.∠CBD与∠D相等吗？请说明理由.
解：∠CBD=∠D。理由如下：
∵∠ABC+∠C=1800（已知）
∴AB∥CD（同旁内角互补，两直线平行）
∴∠D=∠ABD（两直线平行，内错角相等）
∴∠CBD=∠ABD=∠D
1.如图所示 ∠1 =∠2，求证 ： ∠3 =∠4
证明：∵ ∠1 =∠2（已知）
∴a//b (同位角相等,两直线平行)
∴ ∠3 =∠4 (两直线平行，内错角相等)
2.如图，AD∥ BC，∠B＝30°，DB平分∠ADE，则∠DEC的度数.
解：∵AD∥ BC，∠B＝30°（已知）∴∠ADB=∠B＝30°（两直线平行，内错角相等）∵DB平分∠ADE（已知）∴∠ADE=2∠ADB＝60°（角平分线的定义）∴∠DEC=∠ ADE ＝60°(两直线平行，内错角相等）
1.如图，在同一平面内，两条平行的高速l1和l2间有一条“z”型道路连通，其中AB段与高速公路l1成30°角，CD与l2成40°的角，∠ABC=90°，则∠BCD的度数为（　　）
A．60°B．90°C．100°D．110°
2.如图，AB∥CD，AF分别交AB、CD于A、C，CE平分∠DCF，∠1=100°，则∠2= ．
3.如图,一条公路两次拐弯后,和原来的方向相同,也就是拐弯前后的两条路互相平行.第一次拐的角∠B等于1420,第二次拐的角∠C是多少度?为什么？
4.如图,直线DE经过点A,DE//BC,∠B=440，∠C=570.（1）∠DAB 等于多少度？为什么？（2）∠DAC 等于多少度？为什么？
5.巡逻在海上的缉私艇正在向东航行，在A处发现在它的东偏南37°的方向B处有一走私船，缉私艇马上调转船的方向，直逼走私船，并一举截获．这是从雷达上看出港口就在船的正西方，于是船长下令将船头顺时针调转143°直接返港．运用所学知识分析船长所下返航命令的方向是否正确．
解：如图所示：∵∠1=37°，143°与∠ABC互补，∠ABC、∠1是内错角且相等，∴船长下令将船头顺时针调转143°直接返港是正确的．
平行线的性质2：两条平行线被第三条直线所截，内错角相等。简单地说，两直线平行，内错角相等。
平行线的性质3：两条平行线被第三条直线所截，同旁内角互补。简单地说，两直线平行，同旁内角互补。