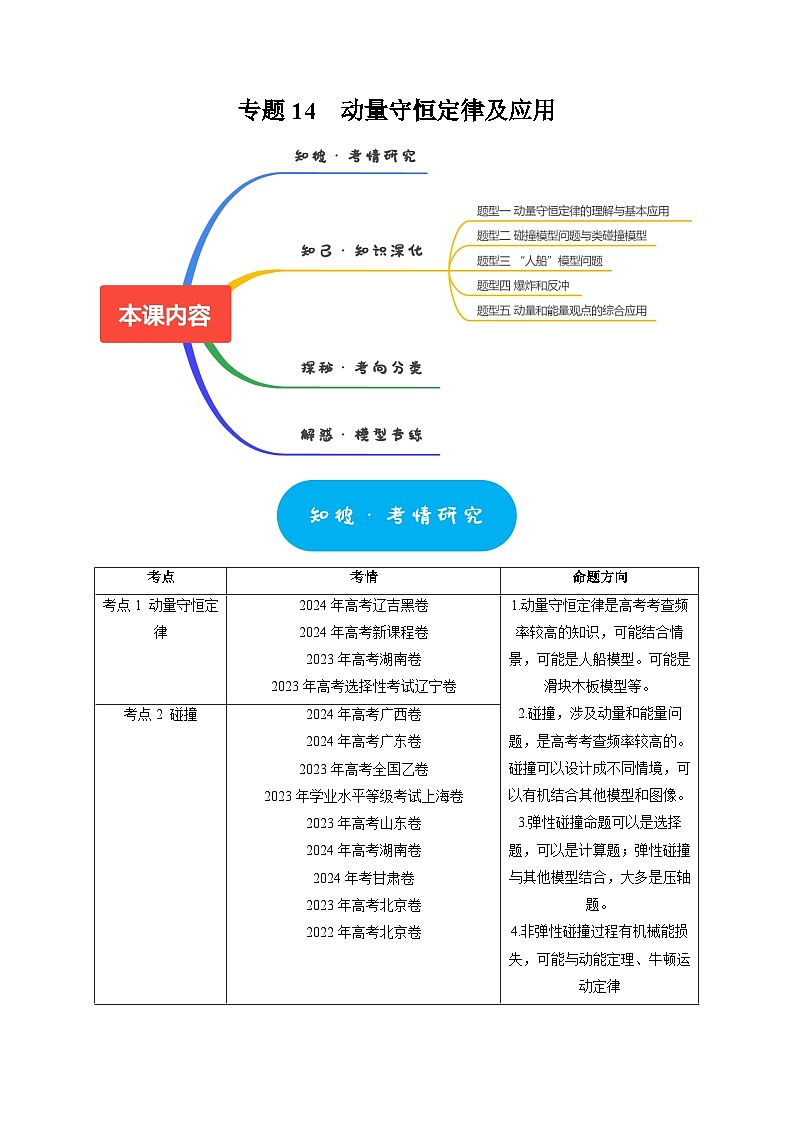
专题14 动量守恒定律及应用-2025年高考物理热点知识讲练与题型归纳（全国通用）

这是一份专题14 动量守恒定律及应用-2025年高考物理热点知识讲练与题型归纳（全国通用），文件包含专题14动量守恒定律及应用教师版-2025年高考物理热点知识讲练与题型归纳全国通用docx、专题14动量守恒定律及应用学生版-2025年高考物理热点知识讲练与题型归纳全国通用docx等2份试卷配套教学资源，其中试卷共40页， 欢迎下载使用。


题型一 动量守恒定律的理解与基本应用
1．内容
如果一个系统不受外力或者所受外力之和为零，这个系统的总动量保持不变，这就是动量守恒定律．
2．适用条件
(1)系统不受外力或所受外力的合力为零，不是系统内每个物体所受的合外力都为零，更不能认为系统处于平衡状态．
(2)近似适用条件：系统内各物体间相互作用的内力远大于它所受到的外力．
(3)如果系统在某一方向上所受外力的合力为零，则系统在该方向上动量守恒．
3．动量守恒定律的不同表达形式
(1)m1v1＋m2v2＝m1v1′＋m2v2′，相互作用的两个物体组成的系统，作用前的动量和等于作用后的动量和．
(2)Δp1＝－Δp2，相互作用的两个物体动量的增量等大反向．
(3)Δp＝0，系统总动量的增量为零．
4．应用动量守恒定律解题的步骤
(1)明确研究对象，确定系统的组成(系统包括哪几个物体及研究的过程)；
(2)进行受力分析，判断系统动量是否守恒(或某一方向上动量是否守恒)；
(3)规定正方向，确定初、末状态动量；
(4)由动量守恒定律列出方程；
(5)代入数据，求出结果，必要时讨论说明．
类型1 系统动量守恒的判断
（2024春•惠山区校级期末）如图所示，小车停在光滑的桌面上，车上固定一个用胶塞塞住封口的试管。试管内充满空气，用车上的酒精灯加热试管尾端。当试管内的空气达到一定温度时，胶塞从试管口喷出，以整个装置为系统，下列说法正确的是（ ）
A．水平方向动量守恒，机械能守恒
B．水平方向动量守恒，机械能不守恒
C．水平方向动量不守恒，机械能守恒
D．水平方向动量不守恒，机械能不守恒
【解答】解：以整个装置为系统，水平方向的合外力为0，所以水平方向系统动量守恒，胶塞从试管口喷出，气体对外做功，内能减少，系统的机械能增加，所以机械能不守恒，故ACD错误，B正确。
故选：B。
（2024春•西安期末）下列四幅图所反映的物理过程中，系统动量守恒的是（ ）
A．只有甲、乙B．只有甲、丙C．只有甲、丁D．只有丙、丁
【解答】解：甲图中子弹与木块组成的系统所受合外力为0，系统动量守恒，乙图中M与N组成的系统所受合外力不为0，系统动量不守恒，丙图中木球与铁球组成的系统所受合外力为0，系统动量守恒，丁图中斜面与木块组成的系统所受合外力不为0，系统动量不守恒，所以系统动量守恒的只有甲、丙，故ACD错误，B正确。
故选：B。
（2024春•武汉期末）如图所示，完全相同的A、B两物块随足够长的水平传送带按图中所示方向匀速运动，A、B间夹有少量炸药。现炸药发生爆炸，则在爆炸及随后的过程中，下列说法正确的是（ ）
A．炸药爆炸过程，A、B两物块组成的系统动量不守恒
B．炸药爆炸过程，A、B两物块组成的系统机械能不能增加
C．在炸药爆炸后至A、B相对传送带静止过程，A、B组成的系统动量守恒
D．在炸药爆炸后至A、B相对传送带静止过程，A、B组成的系统机械能守恒
【解答】解：AB、炸药爆炸过程，A、B两物块组成的系统内力远远大于外力，动量守恒，内能转化为机械能，机械能增加，故AB错误；
CD、在炸药爆炸后至A、B相对传送带静止过程，对AB的两个摩擦力刚好大小相同，方向相反，时间相同，所以冲量是相反的，所以总冲量是0，动量是守恒的，摩擦力做功，机械能不守恒，故C正确，D错误。
故选：C。
类型2 某一方向动量守恒定律的应用
（2024春•大兴区期末）体积相同的小球A和B悬挂于同一高度，静止时两根轻绳竖直，两球球心等高且刚好彼此接触。如图所示，保持B球静止于最低点，拉起A球，将其由距最低点高度为h处静止释放，两球发生碰撞后分离。两球始终在两悬线所决定的竖直平面内运动，悬线始终保持绷紧状态，不计空气阻力。下列说法正确的是（ ）
A．两球从碰撞到分离的过程中，A球减少的动能与B球增加的动能大小一定相等
B．两球从碰撞到分离的过程中，A球动量的变化量与B球动量的变化量大小一定相等
C．两球从碰撞到分离的过程中，A球对B球的冲量大于B球对A球的冲量
D．B球上升的最大高度不可能大于h
【解答】解：A、两球质量未知，由题中条件无法确定是不是弹性碰撞，所以不能确定A球减少的动能与B球增加的动能是不是一定相等，故A错误；
B、两球在最低点碰撞，从碰撞到分离的过程中，动量守恒，AB球的总动量不变，所以A球动量的变化量与B球动量的变化量大小一定相等，方向相反，故B正确；
C、冲量I＝Ft，A对B的作用力和B对A的作用力等大反向，且作用时间相同，所以A球对B球的冲量等于B球对A球的冲量，故C错误；
D、假设AB是弹性碰撞，则有动量守恒和能量守恒得mAvA＝mAv'A+mBv'B，12mAvA2=12mAvA'2+12mBvB'2
联立可得：vA'=mA-mBmA+mBvA，vB'=2mAmA+mBvA
且根据机械能守恒可得：mAgh=12mAvA2，mBgh'=12mBvB'2
联立可得：h'=4mA2(mA+mB)2h
如果mA＞mB，则可得h'＞h，故D错误。
故选：B。
（2023•海淀区校级模拟）如图所示，在光滑的水平面上有一辆平板车。开始时人、锤和车都处于静止状态。人站在车左端，且始终与车保持相对静止，人抡起锤敲打车的左端，每当锤打到车左端时都立即与车具有共同速度。在连续的敲打的过程中，下列说法正确的是（ ）
A．小车将持续地向右运动
B．锤、人和车组成的系统机械能守恒
C．每次锤被向左抡到最高点的时刻，人和车的速度都向右
D．每当锤打到车左端的时刻，人和车立即停止运动
【解答】解：ACD、把人、大锤和车看成一个系统，系统水平方向不受外力，所以系统水平方向动量守恒。由题知系统的总动量为零，所以用大锤连续敲击车的左端时，由水平方向动量守恒可知大锤向左运动时，小车向右运动；大锤向右运动时，小车向左运动，所以车左右往复运动，不会连续向右运动，每当锤打到车左端时都立即与车具有共同速度，人和车立即停止运动，故AC错误，D正确；
B、每当锤打到车左端时都立即与车具有共同速度，系统机械能有损失，可知人和车组成的系统机械能不守恒，故B错误。
故选：D。
（2023春•佛山期末）运动员持球竖直起跳后，如图在空中某位置将球推出，投出的篮球做斜抛运动，下列相关说法正确的是（ ）
A．在空中将球推出的过程中，运动员与篮球组成的系统动量守恒
B．在空中将球推出的过程中，运动员与篮球组成的系统机械能守恒
C．在空中将球推出的过程中，运动员对球作用力的冲量等于球的动量变化量
D．篮球在斜抛运动的上升和下落过程中，所受重力的冲量持续增加
【解答】解：A、在空中将球推出的过程中，运动员与篮球组成的系统所受外力之合，等于运动员和篮球的重力，系统所受外力之合不为零，故运动员与篮球组成的系统动量不守恒，故A错误.
B、系统机械能守恒条件为：只有重力（弹力）做功，在空中将球推出的过程中，有运动员消耗自身能量，产生推力，对球做功，故运动员与篮球组成的系统机械能增加，故B错误。
C、在空中将球推出的过程中，根据动量定理球的动量变化量等于合力的冲量，即等于运动员对球作用力和球重力合力冲量，故C错误。
D、篮球在斜抛运动的上升和下落过程中，所受重力的冲量I＝mgt，随着上升和下落过程时间延长，则篮球所受重力的冲量持续增加，故D正确。
故选：D。
题型二 碰撞模型问题与类碰撞模型
1．碰撞
(1)概念：碰撞是指物体间的相互作用持续时间极短，而物体间相互作用力很大的现象．
(2)特点：在碰撞现象中，一般都满足内力≫外力，可认为相互碰撞的系统动量守恒．
(3)分类
2.碰撞后运动状态可能性判定
(1)动量制约：即碰撞过程中必须受到动量守恒定律的制约，总动量的方向恒定不变，即p1＋p2＝p1′＋p2′.
(2)动能制约：即在碰撞过程中，碰撞双方的总动能不会增加，即Ek1＋Ek2≥Ek1′＋Ek2′
(3)运动制约：即碰撞要受到运动的合理性要求的制约，如果碰前两物体同向运动，则后面物体速度必须大于前面物体的速度，碰撞后原来在前面的物体速度必增大，且大于或等于原来在后面的物体的速度，否则碰撞没有结束；如果碰前两物体是相向运动，而碰后两物体的运动方向不可能都不改变，除非碰后两物体速度均为零．
3.类碰撞模型
类型1 一动一静的弹性碰撞
（2024春•昆明期末）质量为1kg的物块A与另一物块B在光滑水平面上发生正碰，两物块的位置坐标x随时间t变化的图像如图所示。则物块B的质量为（ ）
A．1kgB．2kgC．3kgD．6kg
【解答】解：位移—时间图像的斜率表示滑块的速度，由图像可得两滑块A、B碰撞前后的速度分别为
v1=ΔxΔt=41m/s=4m/s
v2=01m/s＝0、v1′=0-42m/s＝﹣2m/s、v2′=8-42m/s＝2m/s
取碰撞前A的速度方向为正方向，由动量守恒定律有
m1v1＝m1v1′+m2v2′
解得
m2＝3kg
故ABD错误，C正确。
故选：C。
（2024春•武汉期末）光滑水平面上有A、B两球，质量分别为m1、m2，A球以初速度vB与静止的B球发生正碰。下列说法不正确的是（ ）
A．若碰撞是弹性碰撞且碰后A球速度反向，则一定有m1＜m2
B．若碰撞是弹性碰撞且有m1＜m2，则碰后A球速度一定反向
C．若碰撞是非弹性碰撞且碰后A球速度反向，则一定有m1＜m2
D．若碰撞是非弹性碰撞且有m1＜m2，则碰后A球速度一定反向
【解答】解：AB、若发生弹性碰撞，取水平向右为正方向，根据动量守恒定律得：m1v0＝m1v1+m2v2
根据机械能守恒定律得：12m1v02=12m1v12+12m2v22
解得：v1=m1-m2m1+m2v0
若m1＜m2，则有v1＜0，同理：若v1＜0，则m1＜m2，故AB正确；
CD、若碰撞为非弹性碰撞，取水平向右为正方向，根据动量守恒定律得：m1v0＝m1v1+m2v2
根据动能不增加原则有：12m1v02＞12m1v12+12m2v22
解得：v1＞m1-m2m1+m2v0
若m1＜m2可知碰后A球速度不一定反向；
若碰后A球速度反向，即v1＜0，则一定有m1＜m2，故C正确，D错误。
本题选错误的，
故选：D。
（2024•南关区校级模拟）如图所示，用长度均为l的轻质细绳悬挂三个形状相同的弹性小球，质量依次满足m1≫m2≫m3（“≫”表示“远大于”）。将左边第一个小球拉起一定角度θ后释放，则最后一个小球开始运动时的速度约为（ ）
A．2gl(1-csθ)B．22gl(1-csθ)
C．32gl(1-csθ)D．42gl(1-csθ)
【解答】解：设碰撞前瞬间第一个小球的速度为v0，根据机械能守恒定律，有
m1gl(1-csθ)=12m1v02
解得v0=2gl(1-csθ)
设第一个小球与第二个小球碰撞后两个小球的速度分别为v1和v2，取向右为正方向，根据动量守恒定律，有m1v0＝m1v1+m2v2
根据机械能守恒定律，有12m1v02=12m1v12+12m2v22
联立解得v2=2m1m1+m2v0
由于m1≫m2，则v2＝2v0，同理，v3＝2v2，所以v4=4v0=42gl(1-csθ)
故ABC错误，D正确。
故选：D。
类型2 弹性碰撞的“子母球”模型
（多选）（2021秋•东兴区校级月考）如图，质量分别为mA、mB的两个小球A、B静止在地面上方，B球距地面的高度h＝0.8m，A球在B球的正上方。先将B球释放，经过一段时间后再将A球释放。当A球下落t＝0.3s时，刚好与B球在地面上方的P点处相碰，碰撞时间极短，碰后瞬间A球的速度恰为零。已知mB＝3mA，重力加速度大小为g＝10m/s2，忽略空气阻力及碰撞中的动能损失。下列说法正确的是（ ）
A．B球第一次到达地面时的速度为4m/s
B．A、B球在B球向上运动的过程中发生碰撞
C．B球与A球碰撞后的速度为1m/s
D．P点距离地面的高度0.75m
【解答】解：A、B球由释放到第一次到达地面的过程，由动能定理得：
mBgh=12mBvB2，代入数据解得：vB＝4m/s，故A正确；
BC、A球下落过程做自由落体运动，两球碰撞前瞬间A球速度为：
vA＝gt＝10×0.3m/s＝3m/s
设碰撞前后瞬间B球的速度分别为v1，v2。
两球碰撞过程系统动量守恒，取竖直向下为正方向，由动量守恒定律得：
mAvA+mBv1＝mBv2
碰撞中的无动能损失，则有：
12mAvA2+12mBv12=12mBv22
又有：mB＝3mA
代入数据解得：v1＝1m/s，v2＝2m/s
因v1＞0，故碰撞前瞬间B球的速度方向为竖直向下，则A、B球在B球向下运动的过程中发生碰撞。B球与A球碰撞后的速度为2m/s，故BC错误；
D、因小球B与地面碰撞后动能没有损失，故B离开地面上抛的初速度为：v0＝vB＝4m/s
B离开地面到P点的过程，由动能定理得：﹣mBghP=12mBv12-12mBv02
代入数据解得：hP＝0.75m，故D正确。
故选：AD。
在一种新的“子母球”表演中，让同一竖直线上的小球A和小球B分别从距水平地面高度为kh（k＞1）和h的地方同时由静止释放，如图所示。球A的质量为m，球B的质量为4m。设所有碰撞都是弹性碰撞，重力加速度大小为g，忽略球的直径、空气阻力及碰撞时间。
（1）求球B第一次落地时球A的速度大小；
（2）若球B在第一次上升过程中就能与球A相碰，求k的取值范围；
（3）在（2）情形下，要使球A第一次碰后能到达比其释放点更高的位置，求k的取值范围。
【解答】解：（1）AB 两球同时释放做自由落体运动，在B落地过程中A的运动与之完全一致，设所求速度为v0，由运动学公式得：v02=2gh
故，v0=2gh
（2）要想在B上升阶段两球相碰，临界情况是B刚好反跳到出发点时与A相碰，设B下落到地面所用时间为t，则有
h=12gt2
A在2t时间内下落高度
h′=12g（2t）2＝4h
满足要求A的最大高度
h″＝h′+h＝5h
故要是球B在第一次上升过程中就能与球A相碰则应该：1＜k≤5
（3）要使球A第一次碰后能到达比其释放点更高的位置，则临界条件是碰后A球速度恰好等大反向，两物体的v﹣t图象如下图，由弹性碰撞可得碰撞前后，动量守恒，规定向上为正方向，设碰后A球继续向上运动，则：
3mvB﹣mvA＝3mv′B+mvA
由于是弹性碰撞，由碰撞前后能量守恒得：
12×3mvB2+12×mvA2=12×3mv'B2+12mvA2
临界条件v′B＝﹣vB
联立以上可得：
vA＝3vB
从图象可以看出阴影部分面积之和就是A的下落高度和B的反跳高度之和，故kh＝3h，故k＝3
（2014•新课标Ⅰ）如图，质量分别为mA、mB的两个弹性小球A、B静止在地面上方，B球距地面的高度h＝0.8m，A球在B球的正上方，先将B球释放，经过一段时间后再将A球释放，当A球下落t＝0.3s时，刚好与B球在地面上方的P点相碰，碰撞时间极短，碰后瞬间A球的速度恰为零。已知mB＝3mA，重力加速度大小g＝10m/s2，忽略空气阻力及碰撞中的动能损失，求：
（i）B球第一次到达地面时的速度；
（ii）P点距离地面的高度。
【解答】解：（i）B球释放后做自由落体运动，根据自由落体运动位移—速度公式得：
B落地的速度为：v=2gh=2×10×0.8=4m/s⋯①
（ii）设P点距离地面的高度为h′，碰撞前后，A球的速度分别为v1、v1′，B球的速度分别为v2、v2′，由运动学规律可得：
v1＝gt＝10×0.3＝3m/s…②
由于碰撞时间极短，两球碰撞前后动量守恒，动能守恒，规定向下的方向为正，则：
mAv1+mBv2＝mBv2′（碰后A球速度为0）…③
12mAv12+12mBv22=12mBv2′2…④
又知mB＝3mA…⑤
由运动学及碰撞的规律可得B球与地面碰撞前后的速度大小相等，即碰撞后速度大小为4m/s。
则由运动学规律可得h′=42-v222g⋯⑥
联立①～⑥式可得h′＝0.75m。
答：（i）B球第一次到达地面时的速度为4m/s；
（ii）P点距离地面的高度为0.75m。
类型3 类碰撞模型问题
（2024春•青秀区校级期末）一颗子弹水平射入静止在光滑水平地面上M＝1kg的木块后不再穿出，木块的动能增加了8J，设子弹射入木块的过程中子弹所受阻力恒定，下列说法正确的是（ ）
A．木块动量变化量的大小为2kg•m/s
B．子弹对木块做的功与木块对子弹做功的代数和为0J
C．此过程产生的内能可能是6J
D．只增大木块质量，子弹射入木块后仍未穿出，则此过程中系统损失机械能增大
【解答】解：A、根据题意可得12Mv12=8J
解得木块的速度为v1＝4m/s
所以木块动量变化量的大小为Δp＝Mv1＝1×4kg•m/s＝4kg•m/s
故A错误；
B、设子弹射入木块中的深度为d，子弹水平射入木块后，末穿出，到子弹、木块相对静止，木块位移为x，子弹所受阻力为f，则W子弹对木块＝fx
W木块对子弹＝﹣f（x+d）
所以W子弹对木块+W木块对子弹＝﹣fd
故B错误；
C、子弹、木块运动的v﹣t图像如图1所示
图1由于图线与横轴所围区域的面积表示物体发生的位移，由图可知
x＜d
所以W子弹对木块＝fx＝8J＜fd＝Q
即此过程产生的内能大于8J，不可能是6J，故C错误；
D、只增大木块质量，子弹射入木块后仍末穿出，结合牛顿第二定律可知木块的加速度减小，v﹣t图像如图2所示
图2
由图可知，子弹射入木块的深度d增大，产生的内能增大，系统损失的机械能增大，故D正确。
故选：D。
（2024•乐清市校级三模）（机械振动）质量为m的钢板与直立轻弹簧的上端连接，弹簧下端固定在地上。平衡时，弹簧的压缩量为x0，如图所示，一物块从钢板正上方距离为3x0的A处自由落下，打在钢板上并立刻与钢板一起向下运动，但不粘连。它们到达最低点后又向上运动。已知物块质量也为m，弹簧的弹性势能Ep=12kx2，简谐运动的周期T＝2πmk，下列说法正确的是（ ）
A．碰后物块与钢板一起做简谐运动，振幅A＝x0
B．物块与钢板在返回O点前已经分离
C．碰撞刚结束至两者第一次运动到最低点所经历的时间t=2π32x0g
D．运动过程中弹簧的最大弹性势能Epm=32mgx0
【解答】解：A、设物块与钢板碰撞前瞬间物块的速度为v0，由机械能守恒得：
12mv02=3mgx0，解得：v0=6gx0
设碰撞后瞬间两者一起向下运动的初速度为v1，选取向下为正方向，由动量守恒定律得：
mv0＝2mv1，解得：v1=12v0=6gx02
钢板与物块一起做简谐运动，设平衡位置弹簧压缩量为x1，则有：2mg＝kx1
初始对钢板由平衡条件得：mg＝kx0
对比解得：x1＝2x0
设振幅为A，从碰撞的位置到最低点的过程，由机械能守恒定律得：
2mg（x1﹣x0+A）+12⋅2mv12=12k(x1+A)2-12kx02
其中：k=mgx0
联立解得：A＝2x0，故A错误；
B、由A的解答可知，平衡位置弹簧压缩量为2x0，振幅为2x0，由简谐运动规律可知弹簧原长的位置O处是向上的位移最大处，即到达弹簧处于原长的位置时钢板与物块的速度为零，则物块与钢板在返回O点前不会分离，故B错误；
C、碰撞的位置是12A处，由此处第一次到平衡位置的时间为112T，则第一次运动到最低点所经历的时间为：
t=112T+14T=13T=13×2π2mk=2π32x0g，故C正确；
D、弹簧最大压缩量为xm＝x1+A＝4x0，最大的弹性势能：Epm=12k(4x0)2=8mgx0，故D错误。
故选：C。
（2024•陕西模拟）如图所示，用长为L的细线悬挂于O点的小球处于静止状态，质量为m的子弹以速度v0水平射入小球，子弹穿过小球后的速度为34v0，子弹穿过小球后瞬间细线上的张力是子弹射入小球前细线张力的2倍，子弹穿过小球时间极短，重力加速度为g，不考虑小球质量变化，则小球的质量为（ ）
A．v02gLmB．v0gLmC．v04gLmD．v02gLm
【解答】解：子弹穿过小球过程中，子弹和小球组成的系统水平方向动量守恒，设穿过瞬间小球的速度为v，小球的质量为M，向右为正方向则mv0=Mv+34mv0
根据牛顿第二定律，竖直方向有2Mg-Mg=Mv2L
解得M=v04gLm
故ABD错误，C正确。
故选：C。
题型三 “人船”模型问题
1．应用动量守恒定律解题的步骤
(1)明确研究对象，确定系统的组成(系统包括哪几个物体及研究的过程)；
(2)进行受力分析，判断系统动量是否守恒(或某一方向上动量是否守恒)；
(3)规定正方向，确定初、末状态动量；
(4)由动量守恒定律列出方程；
(5)代入数据，求出结果，必要时讨论说明．
（2023秋•海林市校级期末）《三国志》中记载：“置象大船之上，而刻其水痕所至，称物以载之，则校可知矣。”这是著名的曹冲称象的故事。某同学学过动量守恒定律之后，欲利用卷尺测定大船的质量。该同学利用卷尺测出船长为L，然后缓慢进入静止的平行于河岸的船的船尾，再从船尾行走至船头，之后缓慢下船，测出船后退的距离d，已知该同学自身的质量为m，若忽略一切阻力，则船的质量为（ ）
A．LdmB．LL-dmC．L-dLmD．L-ddm
【解答】解：设船的质量为M，人走动时船的速度大小为v，人的速度大小为v′，人从船尾行走至船头所用时间为t。
取船的速度为正方向，则v=dt，v′=L-dt
根据动量守恒定律得：Mv﹣mv′＝0，即Mdt-mL-dt=0，解得：M=L-ddm，故ABC错误，D正确。
故选：D。
（2023秋•福田区校级期末）生命在于运动，运动无限精彩。如图所示，质量为450kg的小船静止在水面上，质量为50kg的人在小船甲板上立定跳远的成绩为2m，不计空气和水的阻力，下列说法正确的是（ ）
A．人起跳后在空中时，船在匀速运动
B．人起跳后在空中时，船仍保持静止
C．人相对地面的跳远成绩为2.2m
D．人在立定跳远过程中，船后退了0.4m
【解答】解：AB.人和船水平方向动量守恒为零，人起跳后在空中水平方向匀速运动，故船匀速运动，故A正确，B错误；
CD.人和船水平方向动量守恒为零，以向右为正，有m人v人﹣m船v船＝0，同时乘以t，则式子变为m人x人﹣m船x船＝0，依题意，x人+x船＝2m，解得，x人＝1.8m，x船＝0.2m，故人相对地面的跳远成绩为1.8m，人在立定跳远过程中，船后退了0.2m，故CD错误。
故选：A。
（多选）（2024•贵州模拟）如图所示，在水平面上放置一半径为R的半圆槽，半圆槽的左、右最高点A、B在同一水平线上、最低点为C，现让一个小球从槽右侧最高点B无初速释放。已知小球和半圆槽的质量分别为m和2m，不计小球与半圆槽和半圆槽与水平地面之间的摩擦，当地的重力加速度为g。则（ ）
A．小球向左运动能达到A点
B．半圆槽向右运动的最大距离为23R
C．半圆槽的运动速度大小可能为3gR2
D．小球经过C点时对半圆槽的压力大小为3mg
【解答】解：A．两物体所构成的系统水平方向动量守恒、运动过程中机械能守恒。小球向左到达最高点时两者共速，设共速时的速度为v，取水平向左为正方向，由动量守恒定律有
0＝（m+2m）v
可得v＝0
由机械能守恒定律有mgR＝mgh
解得h＝R
即小球向左能达到的最高点是A，故A正确；
B．取水平向左为正方向，设小球速度为v1，圆槽速度为v2，由水平方向动量守恒有
0＝mv1+2mv2
可得0＝∑mv1Δt+∑2mv2Δt
即0＝mx1+2mx2
同时x1﹣x2＝﹣2R
可得x2=2R3
故B正确；
C．从B点释放后到C点有，取水平向左为正方向，设在C点小球的速度为v3，圆槽的速度为v4，根据能量和动量守恒有mgR=12mv32+122mv42
0＝mv3+2mv4
解得v3=-233gR，v4=3gR3
则小球到最低点时槽的速度不可能是3gR2，故C错误；
D．小球相对于槽做圆周运动，在最低点槽的加速度为0是惯性参考系，根据牛顿第二定律有
FN-mg=m(v3-v4)2R
解得FN＝4mg
故D错误。
故选：AB。
题型四 爆炸和反冲
（1）爆炸现象的三个规律
①动量守恒：由于爆炸是在极短的时间内完成的，爆炸物体间的相互作用力远远大于受到的外力，所以在爆炸过程中，系统的总动量守恒。
②动能增加：在爆炸过程中，由于有其他形式的能量(如化学能)转化为动能，所以爆炸前后系统的总动能增加。
③位置不变：爆炸的时间极短，因而作用过程中，物体产生的位移很小，一般可忽略不计，可以认为爆炸后仍然从爆炸前的位置以新的动量开始运动。
（2）对反冲现象的说明
①系统内的不同部分在强大内力作用下向相反方向运动，通常用动量守恒来处理。
②反冲运动中，由于有其他形式的能转变为机械能，所以系统的总机械能增加。
（2024•平谷区模拟）可忽略大小的一物体在空中发生爆炸，分裂成三个速率相同但质量不同的物块1、2、3，如图所示，它们的质量大小关系是m1＞m2＞m3，忽略空气阻力，则它们落到水平地面上时速率的大小关系是（ ）
A．物块1的落地速率最大
B．物块2的落地速率最大
C．物块3的落地速率最大
D．三物块的落地速率相同
【解答】解：因为三个物体的初始速率相同设为v0，设落地时的速率为v，根据能量守恒定律可得：mgh+12mv02=12mv2，由此可知三物块的落地速率与质量无关，所以三个物体落地时的速率大小相等，故D正确，ABC错误；
故选：D。
（2023秋•密山市期末）一枚在空中飞行的火箭在某时刻的速度为v0，方向水平，燃料即将耗尽。此时，火箭突然炸裂成两块（如图所示），其中质量为m2的后部分箭体以速率v2沿火箭原方向飞行，若忽略空气阻力及分离前后系统质量的变化，则质量为m1前部分箭体速率v1为（ ）
A．v0﹣v2B．v0+v2
C．v0-m2m1v2D．v0+m2m1(v0-v2)
【解答】解：火箭在爆炸分离时水平方向上动量守恒，规定初速度的方向为正方向，有：（m1+m2）v0＝m1v1+m2v2解得v1=v0+m2m1(v0-v2)，故ABC正确，D正确。
故选：D。
（2024•大庆三模）中国最新的SH﹣16型轮式炮车，应用了大量现代自动化科技，如火控系统接收打击目标、立即调炮、引信装订、弹丸装填、发射药装填等自动射击动作。现一炮车以速度v匀速行驶，炮筒保持水平状态。炮车质量为M，携带一枚质量为m的炮弹，用于发射炮弹的炸药在极短时间内爆炸，将炮弹沿行进方向水平发射出去，由于反冲力作用炮弹飞离炮口时炮车停止运动。炸药质量可忽略不计，求：
（1）炮弹飞离炮口时的速度v；
（2）炸药爆炸释放的能量Q；
（3）设炮弹在炮筒中所受的作用力恒定，已知炮筒长为d，求从发射炮弹到炮弹飞离炮口时，炮车前进的距离。
【解答】解：（1）爆炸过程水平方向动量守恒，炮弹飞出时，炮车停止运动，以运动方向为正方向可得：（M+m）v＝mv1
代入数据解得解得：v1=(M+m)mv；
（2）根据能量守恒，爆炸过程释放的能量：Q=12mv12-12(M+m)v2
代入数据解得：Q=M(m+m)2mv2
（3）设炮弹在炮筒中受到的恒力为F，根据牛顿第二定律，对炮筒有：F＝Ma1，对炮弹有：F＝ma2
炮筒的位移：v2＝2a1L1，炮弹的位移：v12-v2=2a2L2
当炮车和炮弹的相对位移等于d时，炮弹飞离炮口，即：L2﹣L1＝d
代入数据联立解得：L1=mM+md
题型五 动量和能量观点的综合应用
（2024•东西湖区校级模拟）由多个点电荷组成的系统的电势能与它们的电荷量和相对位置有关。如图甲所示，a、b、c三个质量均为m，带等量正电荷的小球，用长度相等不可伸长的绝缘轻绳连接，静置于光滑绝缘水平面上，设此时系统的电势能为E0。现剪断a、c两小球间的轻绳，一段时间后c球的速度大小为v，方向如图乙所示。关于这段时间内的电荷系统，下列说法中正确的是（ ）
A．动量不守恒
B．机械能守恒
C．c球受到的电场力冲量大小为mv
D．图乙时刻系统的电势能为E0-32mv2
【解答】解：A．对系统受力分析，系统受合外力为零，则系统的动量守恒，故A错误；
B．除重力和系统内弹力外，只有电场力做正功，则系统的机械能增加，故B错误；
C．根据动量定理，合力冲量等于动量变化量，c球受到的电场力和细绳拉力的合力的冲量等于c球动量变化，大小为mv，故C错误；
D．由对称性，a球的速度大小也为v，方向与ac连线成30°角斜向左下方，因系统动量守恒，则b球的速度方向垂直ac向上，
如图
由动量守恒定律2×mvsin30°﹣mvb＝0
解得vb＝v
则此时三个小球的动能为Ek=3×12mv2
因系统的电势能和动能之和守恒，则图乙时刻系统的电势能为EP=E0-32mv2
故D正确。
故选：D。
（多选）（2024春•和平区校级期末）如图所示，质量为m的半圆轨道小车静止在光滑的水平地面上，其水平直径AB长度为2R，现将质量也为m的小球从距A点正上方h高处由静止释放，然后由A点经过半圆轨道后从B冲出，在空中能上升的最大高度为34h（不计空气阻力），则该过程（ ）
A．小球和小车组成的系统满足动量守恒
B．小车向左运动的最大距离为R
C．小球离开小车后做斜上抛运动
D．小球和小车组成的系统摩擦生热为14mgh
【解答】解：A、小球与小车组成的系统在水平方向所受合外力为零，系统在水平方向系统动量守恒，故A错误；
B、系统水平方向动量守恒，以向右为正方向，在水平方向，由动量守恒定律得：mv﹣mv′＝0
则有m2R-xt-mxt=0
解得小车的最大位移为x＝R
故B正确；
C、小球与小车组成的系统在水平方向动量守恒，小球由A点离开小车时系统水平方向动量为零，小球与小车水平方向速度为零，小球离开小车后做竖直上抛运动，故C错误；
D、根据动能定理得mg（h-34h）﹣Wf＝0
Wf为小球克服摩擦力做功大小，解得Wf=14mgh
故D正确；
故选：BD。
（2024春•河南期末）如图所示，质量为2m的物块A放在特殊材料（动摩擦因数比较大）制成的水平面上，绕过定滑轮的轻绳一端与物块A相连，另一端吊着质量为m的物块B，处于静止状态。质量为m的圆环C套在轻绳上，在离物块B高度为h处由静止释放，C与B发生弹性碰撞，碰撞时间极短，当B的速度刚好为零时，C与B发生第二次碰撞。已知重力加速度为g，轻绳为不可伸长的刚性绳（即A、B及绳可视为整体），圆环C与绳之间无摩擦，不计空气阻力，求：
（1）圆环C与物块B第一次碰撞前瞬间圆环C的速度大小；
（2）圆环C与物块B碰撞后瞬间，圆环C和物块B的速度大小；
（3）物块A与水平面间的动摩擦因数为多大。
【解答】解：（1）设圆环C与物块B第一次碰撞前瞬间圆环C的速度大小为v0，根据机械能守定律得：mgh=12mv02
解得：v0=2gh
（2）设圆环C与物块B碰撞后瞬间，圆环C和物块B的速度分别为v1、v2，C与B发生弹性碰撞，将A、B作为一个整体，以竖直向下方向为正方向，根据动量守恒定律与机械能守恒定律得：
mv0＝mv1+（m+2m）v2 12mv02=12mv12+12(m+2m)v22
解得：v1=-2gh2，v2=2gh2
（3）设A与水平面间的动摩擦因数为μ，碰撞后B向下做匀减速直线运动的加速度大小为a，则对A、B整体，根据牛顿第二定律得： 2μmg﹣mg＝（m+2m）a
碰撞后C做竖直上抛运动，以竖直向下方向为正方向，对C与B第一次碰撞后的瞬间到第二次碰撞前的瞬间，根据题意，由运动学公式可得：v22=2ax
v2＝at
x=v1t+12gt2
解得：μ＝1考点
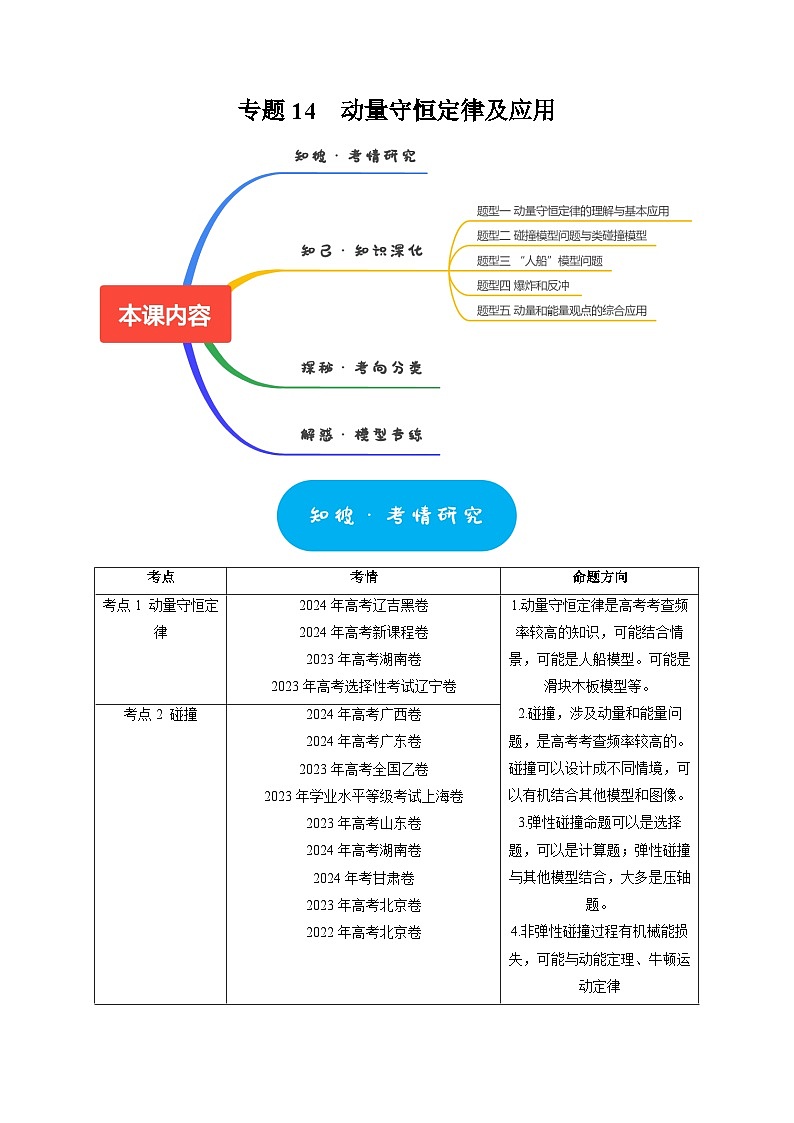
考情
命题方向
考点1 动量守恒定律
2024年高考辽吉黑卷
2024年高考新课程卷
2023年高考湖南卷
2023年高考选择性考试辽宁卷
1.动量守恒定律是高考考查频率较高的知识，可能结合情景，可能是人船模型。可能是滑块木板模型等。
2.碰撞，涉及动量和能量问题，是高考考查频率较高的。碰撞可以设计成不同情境，可以有机结合其他模型和图像。
3.弹性碰撞命题可以是选择题，可以是计算题；弹性碰撞与其他模型结合，大多是压轴题。
4.非弹性碰撞过程有机械能损
失，可能与动能定理、牛顿运动定律
律结合。
考点2 碰撞
2024年高考广西卷
2024年高考广东卷
2023年高考全国乙卷
2023年学业水平等级考试上海卷
2023年高考山东卷
2024年高考湖南卷
2024年考甘肃卷
2023年高考北京卷
2022年高考北京卷
动量是否守恒
机械能是否守恒
弹性碰撞
守恒
守恒
非完全弹性碰撞
守恒
有损失
完全非弹性碰撞
守恒
损失最大