浙教版数学八年级上册期末复习专题第03讲 线段的垂直平分线、角平分线性质、尺规作图（2份，原卷版+解析版）

这是一份浙教版数学八年级上册期末复习专题第03讲 线段的垂直平分线、角平分线性质、尺规作图（2份，原卷版+解析版），文件包含浙教版数学八年级上册期末复习专题第03讲线段的垂直平分线角平分线性质尺规作图3大考点6种解题方法原卷版doc、浙教版数学八年级上册期末复习专题第03讲线段的垂直平分线角平分线性质尺规作图3大考点6种解题方法解析版doc等2份试卷配套教学资源，其中试卷共59页， 欢迎下载使用。
考点考向
一．角平分线的性质
角平分线的性质：角的平分线上的点到角的两边的距离相等．
注意：①这里的距离是指点到角的两边垂线段的长；②该性质可以独立作为证明两条线段相等的依据，有时不必证明全等；③使用该结论的前提条件是图中有角平分线，有垂直角平分线的性质语言：如图，∵C在∠AOB的平分线上，CD⊥OA，CE⊥OB∴CD＝CE
二．线段垂直平分线的性质
（1）定义：经过某一条线段的中点，并且垂直于这条线段的直线，叫做这条线段的垂直平分线（中垂线）垂直平分线，简称“中垂线”．
（2）性质：①垂直平分线垂直且平分其所在线段． ②垂直平分线上任意一点，到线段两端点的距离相等． ③三角形三条边的垂直平分线相交于一点，该点叫外心，并且这一点到三个顶点的距离相等．
三．作图—基本作图
基本作图有：
（1）作一条线段等于已知线段．
（2）作一个角等于已知角．
（3）作已知线段的垂直平分线．
（4）作已知角的角平分线．
（5）过一点作已知直线的垂线．
四．作图—复杂作图
复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．
解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．
五．作图—应用与设计作图
应用与设计作图主要把简单作图放入实际问题中．
首先要理解题意，弄清问题中对所作图形的要求，结合对应几何图形的性质和基本作图的方法作图．
六．作图—代数计算作图
代数计算作图是实际问题中要求所作图形具备一定的条件，如角的度数或边的长度．
（1）根据题意计算出图形所具备的条件，边长，角度等，在网格纸上作图或利用圆规和直尺作图．
（2）直接利用尺规作图做出符合题意的图形．如在数轴上找到表示无理数的点．
要熟悉几何图形的性质和5种基本作图的步骤，才能灵活运用熟练作图．
考点精讲
一．角平分线的性质（共5小题）
1．（2021秋•温岭市期末）如图，OP平分∠AOB，E为OA上一点，OE＝4，P到OB的距离是2，则△OPE的面积为（ ）
A．2B．3C．4D．8
2．（2021秋•北仑区期中）如图，AD是△ABC的角平分线，DE⊥AB于点E，S△ABC＝9，DE＝2，AB＝5，则AC的长是（ ）
A．2B．3C．4D．5
3．（2021秋•东阳市期末）如图，在△ABC中，∠C＝90°，以A为圆心，任意长为半径画弧，分别交AC，AB于点M，N，再分别以M，N为圆心，大于MN长为半径画弧，两弧交于点O，作射线AO，交BC于点E．已知CE＝3，BE＝5，则AC的长为（ ）
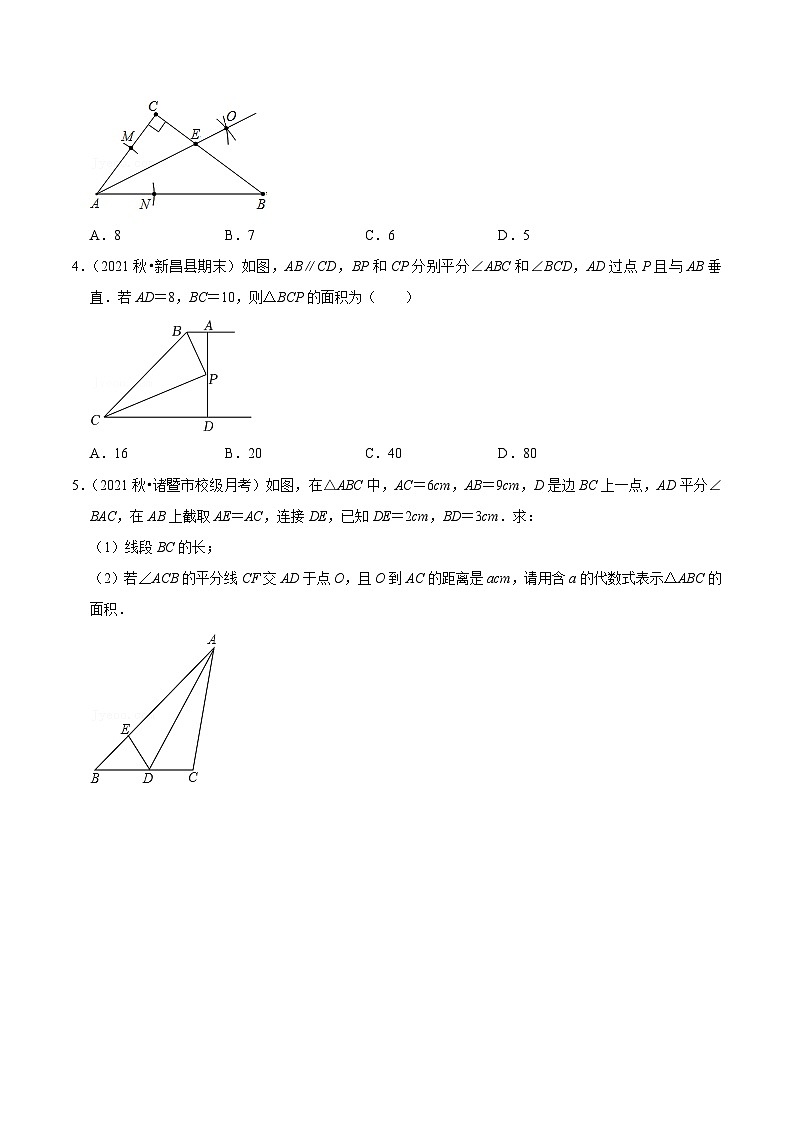
A．8B．7C．6D．5
4．（2021秋•新昌县期末）如图，AB∥CD，BP和CP分别平分∠ABC和∠BCD，AD过点P且与AB垂直．若AD＝8，BC＝10，则△BCP的面积为（ ）
A．16B．20C．40D．80
5．（2021秋•诸暨市校级月考）如图，在△ABC中，AC＝6cm，AB＝9cm，D是边BC上一点，AD平分∠BAC，在AB上截取AE＝AC，连接DE，已知DE＝2cm，BD＝3cm．求：
（1）线段BC的长；
（2）若∠ACB的平分线CF交AD于点O，且O到AC的距离是acm，请用含a的代数式表示△ABC的面积．
二．线段垂直平分线的性质（共8小题）
6．（2021秋•海曙区期末）如图，△ABC中，AB的垂直平分线分别交AB、BC于点D、E，AC的垂直平分线分别交AC、BC于点F、G，若∠EAG＝40°，则∠BAC的度数是（ ）
A．140°B．130°C．120°D．110°
7．（2021秋•温州期末）如图，已知线段AB，以点A，B为圆心，5为半径作弧相交于点C，D．连结CD，点E在CD上，连结CA，CB，EA，EB．若△ABC与△ABE的周长之差为4，则AE的长为（ ）
A．1B．2C．3D．4
8．（2021秋•余杭区月考）如图，在△ABC中，DE是AC的中垂线，分别交AC、AB于点D、E，若△BCE的周长为8，BC＝3，求AB的长．
9．（2021秋•义乌市期中）如图，已知△ABC中，边AB、AC的垂直平分线分别交BC于E、F，若∠EAF＝90°，AF＝3，AE＝4．
（1）求边BC的长；
（2）求出∠BAC的度数．
10．（2021秋•柯桥区月考）已知：如图，△ABC中，∠A＝90°，BC的垂直平分线DE交BC于点E，交AC于点D．
（1）若∠C＝35°，求∠DBA的度数；
（2）若△ABD的周长为30，AC＝18，求AB的长．
11．（2021秋•余杭区期中）如图，△ABC中，∠BAC＝130°，AB，AC的垂直平分线分别交BC于点E，F，与AB，AC分别交于点D，G，则∠EAF的度数为（ ）
A．65°B．60°C．70°D．80°
12．（2021秋•上城区期中）如图，在△ABC中，AD是BC边上的高线，AD的垂直平分线分别交AB，AC于点E，F．
（1）若∠DAC＝20°，求∠FDC的度数；
（2）试判断∠B与∠AED的数量关系，并说明理由．
13．（2021秋•西湖区期末）如图，线段AB，BC的垂直平分线l1、l2相交于点O．若∠1＝40°，则∠AOC＝（ ）
A．50°B．80°C．90°D．100°
三．作图—基本作图（共4小题）
14．（2021秋•鄞州区期中）如图，在△ABC中，∠B＝65°，∠C＝30°，分别以点A和点C为圆心，大于AC的长为半径画弧，两弧相交于点M、N，作直线MN，交BC于点D，连接AD，则∠BAD的度数为（ ）
A．45°B．55°C．60°D．65°
15．（2021秋•诸暨市期末）下列尺规作图分别表示：①作一个角的平分线，②作一条线段的垂直平分线．其中作法正确的是（ ）
A．①B．②C．①②D．无
16．（2021秋•新昌县期末）如图，已知△ABC．
（1）请用直尺和圆规作∠ABC的角平分线BD，交AC于点D．（保留作图痕迹，不写作法）
（2）在（1）的条件下，若∠A＝100°，∠C＝28°，求∠BDA的度数．
17．（2021秋•余姚市期末）如图，在△ABC中，CE⊥AB于点E．
（1）用尺规作BD⊥AC，垂足为点D．（不写作法，保留痕迹）
（2）在（1）所画的图中，若BE＝CD．求证：AB＝AC．
四．作图—复杂作图（共5小题）
18．（2021秋•临海市期末）如图，已知△ABC，点D在边AB上．
（1）求作点D，使点D到点B，C的距离相等；（尺规作图，保留作图痕迹，不写作法）
（2）连接DC，已知∠B＝32°，求∠ADC的度数．
19．（2021秋•缙云县期末）（拓展创新）如图所示，正方形网格中的每个小正方形边长都是1，每个小格的顶点叫格点，以格点以顶点分别按下列要求画三角形．
（1）使三角形的三边长分别为3，2，；（在图①中画一个即可）
（2）使三角形为钝角三角形且面积为4．（在图②中画一个即可）
20．（2021秋•新昌县期中）如图，在△ABC中，AB＞AC，按以下步骤作图：分别以点B和点C为圆心，大于BC长为半径作圆弧，两弧相交于点M和点N，作直线MN交AB于点D；连结CD．
（1）则MN是BC的 线．
（2）若AB＝8，AC＝4，求△ACD的周长．
21．（2021秋•西湖区校级期中）如图，已知△ABC．
（1）尺规作图：①作出△ABC的角平分线CD；②作出BC的中垂线交AB于点E．
（2）连结CE，若∠ABC＝60°，∠A＝40°，则∠DCE＝ ．
22．（2021秋•拱墅区期中）如图，△ABC中，AC＞AB．
（1）作AB边的垂直平分线交BC于点P，作AC边的垂直平分线交BC于点Q，连接AP，AQ．（尺规作图，保留作图痕迹，不需要写作法）
（2）在（1）的条件下，若BC＝14，求△APQ的周长．
五．作图—应用与设计作图（共6小题）
23．（2021秋•临海市期末）如图，在5×5的网格纸中，△ABC的三个顶点都在格点上．请仅用直尺，按要求画图．
（1）在图1中画出过点B的直线l，使其平分△ABC的面积；
（2）在图2中画出线段BD，使其平分∠ABC，且点D在格点上．
24．（2021秋•椒江区期末）如图，两条公路OA，OB相交于点O，在∠AOB内部有两个村庄C，D．为方便群众接种新冠疫苗，该地决定在∠AOB内部再启动一个方舱式接种点P，要求同时满足：
（1）到两条公路OA，OB的距离相等．
（2）到两村庄C，D的距离相等．
请你用直尺和圆规作出接种点P的位置（保留作图痕迹）．
25．（2021秋•宁波期末）定义：如果三角形的两个内角α和β满足α+2β＝90°，那么我们称这样的三角形为“类直角三角形”．
如图，在△ABC中，∠C＝90°，AC＝8，BC＝6．请把这个三角形分割成两个三角形，使得其中一个为“类直角三角形”，并求出这个“类直角三角形”的面积．（备注：要求尺规作图）
26．（2021秋•婺城区校级月考）如图，在7×6的方格中，△ABC的顶点均在格点上．试按要求画出线段EF（E，F均为格点），各画出一条即可．
27．（2021春•南岗区校级月考）如图，网格中的每个小正方形的边长都是2，线段交点称做格点．
（1）画出△ABC的高CD；
（2）连接格点，用一条线段将图中△ABC分成面积相等的两部分；
（3）直接写出△ABC的面积是 ．
28．（2021春•鼓楼区校级月考）我们知道，三角形具有性质：三条角平分线相交于一点，三条中线相交于一点．事实上，三角形还具有性质：三条高所在直线相交于一点．如图，在由小正方形组成的4×3的网格中，三角形的顶点都在小正方形的格点上．请运用上述三角形的性质，在该网格中，仅用无刻度的直尺，作出AC边上的高BH，再作出BC边上的高AK．（不写作法，保留作图痕迹）
六．作图—代数计算作图（共1小题）
29．（2021秋•诸暨市期中）如图，在5×5的正方形网格中，每个小正方形的边长都为1，请在所给网格中解答下面问题．
（1）图中线段AB的两端点都落在格点（即小正方形的顶点）上，求出AB的长度；
（2）再以AB为一边画一个等腰三角形ABC，使点C在格点上，且另两边的长都是无理数；
（3）请直接写出符合（2）中条件的等腰三角形ABC的顶点C的个数．
一、单选题
1．（2021·衢州市实验学校教育集团（衢州学院附属学校教育集团）八年级期末）如图，在上分别截取，使，再分别以点为圆心，以大于的长为半径作弧，两弧在内交于点，作射线就是的角平分线．这是因为连结，可得到，根据全等三角形对应角相等，可得．在这个过程中，得到的条件是（ ）
A．B．C．D．
2．（2021·浙江八年级期末）如图是用直尺和圆规作一个角等于已知角的示意图，说明的依据是（ ）
A．B．C．D．
3．（2020·浙江八年级期末）内找一点P，使P到B、C两点的距离相等，并且P到C的距离等于A到C的距离．下列尺规作图正确的是（ ）
A．B．
C．D．
4．（2020·浙江八年级期末）如图，在的两边上，分别取，再分别过点、作、的垂线，交点为，画射线，则平分的依据是（ ）
A．B．C．D．
5．（2020·浙江八年级期末）如图，已知，求作一点P，使P到的两边的距离相等，且、下列确定P点的方法正确的是（ ）
A．P为两角平分线的交点B．P为两边上的高的交点
C．P为两边的垂直平分线的交点D．P为的角平分线与的垂直平分线的交点
二、填空题
6．（2019·浙江八年级期末）如图，依据尺规作图的痕迹，计算∠α=________°．
7．（2019·浙江杭州·八年级月考）用直尺和圆规作一个角等于已知角的示意图如下，则要说明，需要证明，则两个三角形全等的依据是________（写出全等简写）．
8．（2018·浙江全国·）用直尺和圆规作一个角的平分线的示意图如图所示，则能说明∠AOC＝∠BOC的依据是_______．
9．（2020·浙江高照实验学校八年级月考）如图，在ABC中，∠C＝90°，∠B＝30°，以点A为圆心，任意长为半径画弧分别交AB、AC于点M和N，再分别以M、N为圆心，大于MN的长为半径画弧，两弧交于P，连接AP并延长交BC于点D，则∠ADB＝_____度．
10．（2019·浙江杭州市·）尺规作图作∠AOB的平分线方法如下：以O为圆心，任意长为半径画弧交OA，OB于C，D，再分别以点C，D为圆心，以大于长为半径画弧，两弧交于点P，作射线OP. 由作法得△OCP≌△ODP的根据是_________．
三、解答题
11．（2019·浙江八年级期中）如图，在△ABC中，AB＝AC，∠ABC＝76°．
（1）用直尺和圆规作∠ABC的平分线BD交AC于点D（保留作图痕迹，不要求写作法）；
（2）在（1）中作出∠ABC的平分线BD后，求∠BDC的度数．
12．（2021·浙江八年级期末）电信部门要修建一座电视信号发射塔，如图，按照设计要求，发射塔到两个城镇A，B的电网必须相等，到两条高速公路m和n的距离也必须相等，发射塔应修建在什么位置，从图中标出．（保留作图痕迹，说明理由）
13．（2020·浙江）已知，用尺规作图：
（1）作边上的中线；
（2）画边上的高．
14．（2019·浙江宁波·八年级期中）某小区为方便M、N两幢住宅楼的住户投放分类后的垃圾，拟在小区主路的交叉区域内设置一个垃圾投放点P，现要求P点到两条道路的距离相等，且使，请你通过尺规作图找出这一P点（不写作法，保留作图痕迹）
15．（2020·浙江八年级期末）已知：线段c和求作：，使得（不写作法，但保留作图痕迹）
16．（2020·浙江）已知线段及锐角，用直尺和圆规作，使，．
17．（2020·浙江）如图，线段，利用直尺和圆规按照下列要求作出图形．（保留作图痕迹，不要求写作法）
（1）作一个等边三角形，边长为；
（2）在第（1）题的图中，作一个，使．
18．（2020·浙江八年级期末）如图，和点.在内部，试求作一点，使得点到两边的距离相等，同时到点，的距离也相等.（不写作法，保留作图痕迹）
19．（2021·浙江八年级期末）如图，已知，请按下列要求作图：
（1）作边上的中线．
（2）用直尺和圆规作的角平分线．
（3）用直尺和圆规作，使（使点D与A对应，点E与B对应，点F与C对应）．
20．（2020·浙江八年级期中）如图，已知
（1）用直尺和圆规按下列要求作图：（保留作图痕迹）在上作点D，使点D到和的距离相等；过点B作交的延长线于E；
（2）若，垂足为F，证明．