浙教版数学八年级上册期末复习专题第02讲 全等三角形的概念、性质、判定（3大考点5种解题方法）（2份，原卷版+解析版）

这是一份浙教版数学八年级上册期末复习专题第02讲 全等三角形的概念、性质、判定（3大考点5种解题方法）（2份，原卷版+解析版），文件包含浙教版数学八年级上册期末复习专题第02讲全等三角形的概念性质判定3大考点5种解题方法原卷版doc、浙教版数学八年级上册期末复习专题第02讲全等三角形的概念性质判定3大考点5种解题方法解析版doc等2份试卷配套教学资源，其中试卷共68页， 欢迎下载使用。
一．全等图形
（1）全等形的概念
能够完全重合的两个图形叫做全等形．
（2）全等三角形
能够完全重合的两个三角形叫做全等三角形．
（3）三角形全等的符号
“全等”用符号“≌”表示．注意：在记两个三角形全等时，通常把对应顶点写在对应位置上．
（4）对应顶点、对应边、对应角
把两个全等三角形重合到一起，重合的顶点叫做对应顶点；重合的边叫做对应边；重合的角叫做对应角．
二．全等三角形的性质
（1）性质1：全等三角形的对应边相等
性质2：全等三角形的对应角相等
说明：①全等三角形的对应边上的高、中线以及对应角的平分线相等
②全等三角形的周长相等，面积相等
③平移、翻折、旋转前后的图形全等
（2）关于全等三角形的性质应注意
①全等三角形的性质是证明线段和角相等的理论依据，应用时要会找对应角和对应边．
②要正确区分对应边与对边，对应角与对角的概念，一般地：对应边、对应角是对两个三角形而言，而对边、对角是对同一个三角形的边和角而言的，对边是指角的对边，对角是指边的对角．
三．全等三角形的判定
（1）判定定理1：SSS﹣﹣三条边分别对应相等的两个三角形全等．
（2）判定定理2：SAS﹣﹣两边及其夹角分别对应相等的两个三角形全等．
（3）判定定理3：ASA﹣﹣两角及其夹边分别对应相等的两个三角形全等．
（4）判定定理4：AAS﹣﹣两角及其中一个角的对边对应相等的两个三角形全等．
（5）判定定理5：HL﹣﹣斜边与直角边对应相等的两个直角三角形全等．
方法指引：全等三角形的5种判定方法中，选用哪一种方法，取决于题目中的已知条件，若已知两边对应相等，则找它们的夹角或第三边；若已知两角对应相等，则必须再找一组对边对应相等，且要是两角的夹边，若已知一边一角，则找另一组角，或找这个角的另一组对应邻边．
四．全等三角形的判定与性质
（1）全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．
（2）在应用全等三角形的判定时，要注意三角形间的公共边和公共角，必要时添加适当辅助线构造三角形．
五．全等三角形的应用
（1）全等三角形的性质与判定综合应用
用全等寻找下一个全等三角形的条件，全等的性质和判定往往是综合在一起应用的，这需要认真分析题目的已知和求证，分清问题中已知的线段和角与所证明的线段或角之间的联系．
（2）作辅助线构造全等三角形
常见的辅助线做法：①把三角形一边的中线延长，把分散条件集中到同一个三角形中是解决中线问题的基本规律．②证明一条线段等于两条线段的和，可采用“截长法”或“补短法”，这些问题经常用到全等三角形来证明．
（3）全等三角形在实际问题中的应用
一般方法是把实际问题先转化为数学问题，再转化为三角形问题，其中，画出示意图，把已知条件转化为三角形中的边角关系是关键．
考点精讲
一．全等图形（共3小题）
1．（2021秋•襄州区校级月考）下列说法正确的是（ ）
A．形状相同的两个三角形全等
B．面积相等的两个三角形全等
C．完全重合的两个三角形全等
D．所有的等边三角形全等
【分析】根据全等形的概念：能够完全重合的两个图形叫做全等形，以及全等三角形的判定定理可得答案．
【解答】解：A、形状相同的两个三角形全等，说法错误，应该是形状相同且大小也相同的两个三角形全等；
B、面积相等的两个三角形全等，说法错误；
C、完全重合的两个三角形全等，说法正确；
D、所有的等边三角形全等，说法错误；
故选：C．
【点评】此题主要考查了全等图形，关键是掌握全等形的概念．
2．（2021秋•义乌市期中）如图，方格纸中是9个完全相同的正方形，则∠1+∠2的值为 90° ．
【分析】利用全等三角形的判定定理SAS证得△ABC≌△EDF，则其对应角相等：∠3＝∠1，则∠2+∠3＝∠2+∠1＝90°．
【解答】解：如图，在△ABC与△EDF中，
，
∴△ABC≌△EDF（SAS），
∴∠3＝∠1，
则∠2+∠3＝∠2+∠1＝90°．
故答案为：90°．
【点评】本题考查的是全等形的识别、全等图形的基本性质，属于较容易的基础题．
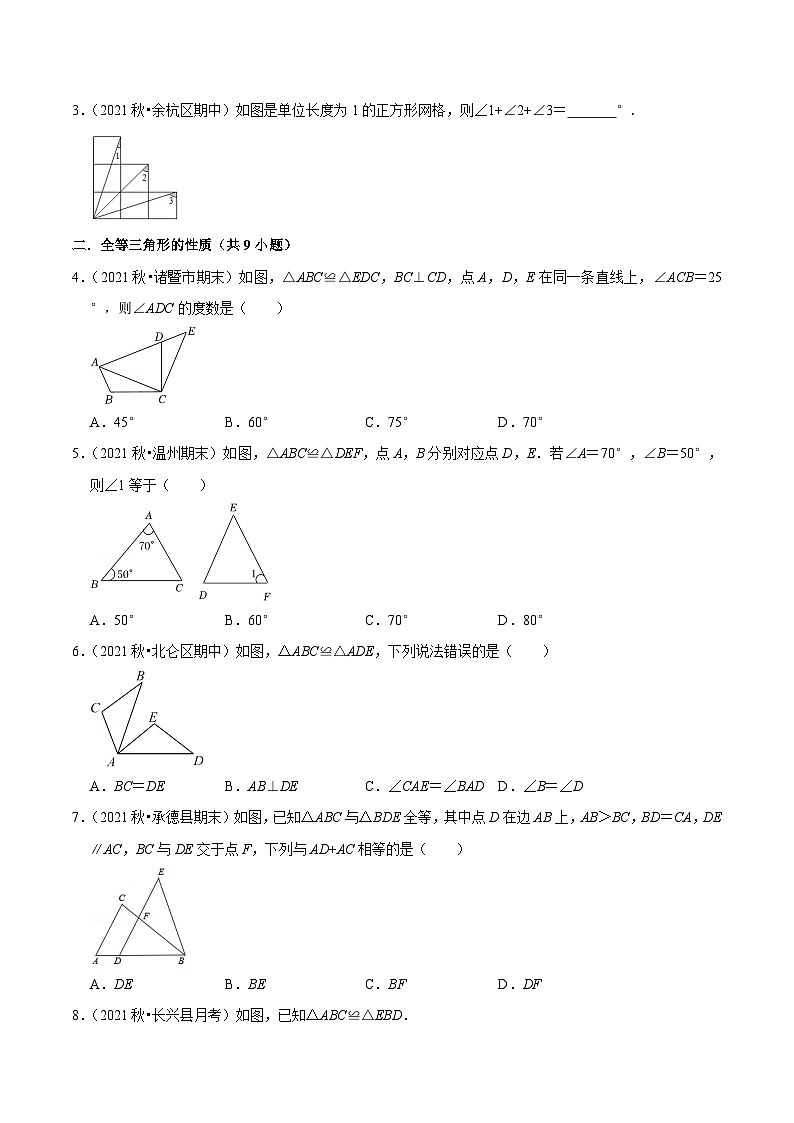
3．（2021秋•余杭区期中）如图是单位长度为1的正方形网格，则∠1+∠2+∠3＝ 135 °．
【分析】首先证明△ABC≌△AEF，然后证明∠1+∠3＝90°，再根据等腰直角三角形的性质可得∠2＝45°，进而可得答案．
【解答】解：
在△ABC和△AEF中，
，
∴△ABC≌△AEF（SAS），
∴∠4＝∠3，
∵∠1+∠4＝90°，
∴∠1+∠3＝90°，
∵AD＝MD，∠ADM＝90°，
∴∠2＝45°，
∴∠1+∠2+∠3＝135°，
故答案为：135．
【点评】此题主要考查了全等三角形的判定和性质，以及等腰直角三角形的性质，关键是掌握全等三角形对应角相等．
二．全等三角形的性质（共9小题）
4．（2021秋•诸暨市期末）如图，△ABC≌△EDC，BC⊥CD，点A，D，E在同一条直线上，∠ACB＝25°，则∠ADC的度数是（ ）
A．45°B．60°C．75°D．70°
【分析】根据全等三角形的性质和三角形内角和解答即可．
【解答】解：∵△ABC≌△EDC，BC⊥CD，
∴∠DCE＝∠ACB＝25°，∠BCD＝∠ACE＝90°，AC＝CE，
∴∠ACD＝90°﹣25°＝65°，
∵点A，D，E在同一条直线上，
∴∠ADC+∠EDC＝180°，
∵∠EDC+∠E+∠DCE＝180°，
∴∠ADC＝∠E+25°，
∵∠ACE＝90°，AC＝CE，
∴∠DAC+∠E＝90°，∠E＝∠DAC＝45°，
在△ADC中，∠ADC+∠DAC+∠DCA＝180°，
即45°+65°+∠ADC＝180°，
解得：∠ADC＝70°，
故选：D．
【点评】此题考查全等三角形的性质，关键是根据全等三角形的性质和三角形内角和解答．
5．（2021秋•温州期末）如图，△ABC≌△DEF，点A，B分别对应点D，E．若∠A＝70°，∠B＝50°，则∠1等于（ ）
A．50°B．60°C．70°D．80°
【分析】根据三角形内角和定理求出∠C，根据全等三角形的对应角相等解答即可．
【解答】解：在△ABC中，∠A＝70°，∠B＝50°，
则∠C＝180°﹣∠A﹣∠B＝180°﹣70°﹣50°＝60°，
∵△ABC≌△DEF，
∴∠1＝∠C＝60°
故选：B．
【点评】本题考查的是全等三角形的性质、三角形内角和定理，掌握全等三角形的对应角相等是解题的关键．
6．（2021秋•北仑区期中）如图，△ABC≌△ADE，下列说法错误的是（ ）
A．BC＝DEB．AB⊥DEC．∠CAE＝∠BADD．∠B＝∠D
【分析】依据全等三角形的对应边相等，全等三角形的对应角相等进行判断即可．
【解答】解：∵△ABC≌△ADE，
∴∠B＝∠D，DE＝CB，∠CAE＝∠BAD．
故选：B．
【点评】本题主要考查的是全等三角形的性质，熟练掌握全等三角形的性质是解题的关键．
7．（2021秋•承德县期末）如图，已知△ABC与△BDE全等，其中点D在边AB上，AB＞BC，BD＝CA，DE∥AC，BC与DE交于点F，下列与AD+AC相等的是（ ）
A．DEB．BEC．BFD．DF
【分析】根据全等三角形的性质得出AC＝DB，进而解答即可．
【解答】解：∵DE∥AC，
∴∠A＝∠EDB，
∵△ABC与△BDE全等，
∴BC＝BE，AC＝DB，AB＝DE，
∴AC+AD＝DB+AD＝AB＝DE，
故选：A．
【点评】此题考查全等三角形的性质，关键是根据全等三角形的对应边相等解答．
8．（2021秋•长兴县月考）如图，已知△ABC≌△EBD．
（1）若BE＝6，BD＝4，求线段AD的长；
（2）若∠E＝30°，∠B＝48°，求∠ACE的度数．
【分析】（1）根据全等三角形的性质，由△ABC≌△EBD，得AB＝EB＝6，那么AD＝AB﹣BD＝2．
（2）根据全等三角形的性质，由△ABC≌△EBD，得∠A＝∠E＝30°．根据三角形外角的性质，得∠ACE＝∠A+∠B＝78°．
【解答】解：（1）∵△ABC≌△EBD，
∴AB＝EB＝6．
∴AD＝AB﹣BD＝6﹣4＝2．
（2）∵△ABC≌△EBD，
∴∠A＝∠E＝30°．
∴∠ACE＝∠A+∠B＝30°+48°＝78°．
【点评】本题考查全等三角形的性质、三角形外角的性质，熟练掌握全等三角形的性质、三角形外角的性质是解决本题的关键．
9．（2021秋•余杭区月考）如图，△ADF≌△BCE，∠B＝40°，∠F＝22°，BC＝2cm，CD＝1cm．求：
（1）∠1的度数；
（2）AC的长．
【分析】（1）根据全等三角形的性质得出∠E＝∠F＝22°，再根据三角形的外角性质求出答案即可；
（2）根据全等三角形的性质得出AD＝BC＝2cm，再求出AC即可．
【解答】解：（1）∵△ADF≌△BCE，∠F＝22°，
∴∠E＝∠F＝22°，
∵∠B＝40°，
∴∠1＝∠B+∠E＝40°+22°＝62°；
（2）∵△ADF≌△BCE，BC＝2cm，
∴AD＝BC＝2cm，
∵DC＝1cm，
∴AC＝AD+DC＝2+1＝3（cm）．
【点评】本题考查了全等三角形的性质和三角形外角性质，能熟记全等三角形的性质是解此题的关键，注意：全等三角形的对应边相等，对应角相等．
10．（2021秋•大化县期中）如图所示，已知△ABD≌△CFD，AD⊥BC于D．
（1）求证：CE⊥AB；
（2）已知BC＝7，AD＝5，求AF的长．
【分析】（1）由△ABD≌△CFD，得出∠BAD＝∠DCF，再利用三角形内角和即可得出答案；
（2）根据全等三角形的性质得出AD＝DC，即可得出BD＝DF，进而解决问题．
【解答】（1）证明：∵△ABD≌△CFD，
∴∠BAD＝∠DCF，
又∵∠AFE＝∠CFD，
∴∠AEF＝∠CDF＝90°，
∴CE⊥AB；
（2）解：∵△ABD≌△CFD，
∴BD＝DF，
∵BC＝7，AD＝DC＝5，
∴BD＝BC﹣CD＝2，
∴AF＝AD﹣DF＝5﹣2＝3．
【点评】此题考查了全等三角形的性质，熟练应用全等三角形的性质是解决问题的关键．
11．（2021秋•青田县期末）如图，已知△ABC≌△DEF，B，E，C，F在同一条直线上．若BF＝8cm，BE＝2cm，则CE的长度（ ）cm．
A．5B．4C．3D．2
【分析】根据全等三角形的性质得出BC＝EF，求出BE＝CF＝2cm，再求出答案即可．
【解答】解：∵△ABC≌△DEF，
∴BC＝EF，
∴BC﹣CE＝EF﹣CE，
∴BE＝CF，
∵BE＝2cm，
∴CF＝BE＝2cm，
∵BF＝8cm，
∴CE＝BF﹣BE﹣CF＝8﹣2﹣2＝4（cm），
故选：B．
【点评】本题考查了全等三角形的性质，能熟记全等三角形的对应边相等是解此题的关键．
12．（2021秋•诸暨市校级月考）如图，△ABC≌△ADE，且∠CAD＝35°，∠B＝∠D＝20°，∠EAB＝105°，求∠BFD和∠BED的度数．
【分析】根据△ABC≌△ADE，进而得到∠EAD＝∠CAB，结合∠CAD＝35°，即可求出∠EAD和∠CAB的度数，再结合外角的性质即可求出所求角的度数．
【解答】解：∵△ABC≌△ADE，
∴∠EAD＝∠CAB，
又∵且∠CAD＝35°，∠EAB＝105°，
∴∠EAD+∠DAC+∠CAB＝∠EAB＝105°，
∴∠EAD＝∠DAC＝∠CAB＝35°，
∴∠DFB＝∠DAB+∠B＝70°+20°＝90°，
∠BED＝∠BFD﹣∠D＝90°﹣20°＝70°．
【点评】本题主要考查了全等三角形的性质，解题的关键是掌握三角形外角的性质，此题难度不大．
三．全等三角形的判定（共8小题）
13．（2021•普陀区校级开学）如图，已知AB＝AD，AE＝AC，∠DAB＝∠EAC．求证：△ACD≌△AEB．
【分析】先证明∠DAC＝∠BAE，然后根据“SAS”可判断△ACD≌△AEB．
【解答】证明：∵∠DAB＝∠EAC，
∴∠DAB+∠BAC＝∠EAC+∠BAC，
即∠DAC＝∠BAE，
在△ACD和△AEB中，
，
∴△ACD≌△AEB（SAS）．
【点评】本题考查了全等三角形的判定：熟练掌握全等三角形的5种判定方法是解决问题的关键，选用哪一种方法，取决于题目中的已知条件．
14．（2021秋•湖州期末）我国传统工艺中，油纸伞制作非常巧妙，其中蕴含着数学知识．如图是油纸伞的张开示意图，AE＝AF，GE＝GF，则△AEG≌△AFG的依据是（ ）
A．SASB．ASAC．AASD．SSS
【分析】根据全等三角形的判定定理推出即可．
【解答】解：在△AEG和△AFG中，
，
∴△AEG≌△AFG（SSS），
故选：D．
【点评】本题考查了全等三角形的判定定理，能熟记全等三角形的判定定理是解此题的关键，注意：全等三角形的判定定理有SAS，ASA，AAS，SSS，两直角三角形全等还有HL等．
15．（2021秋•上城区期末）如图，已知∠DBC＝∠ACB，添加一个条件不能证明△ABC≌△DCB的是（ ）
A．AB＝CDB．AC＝BDC．∠ABD＝∠ACDD．∠A＝∠D
【分析】根据全等三角形的判定方法对各选项进行判断．
【解答】解：∵∠DBC＝∠ACB，BC＝CB，
∴当添加AC＝BD时，根据“SAS”判断△ABC≌△DCB；
当添加∠ABC＝∠ACD时，则∠ABC＝∠DCB，根据“ASA”判断△ABC≌△DCB；
当添加∠A＝∠D时，根据“AAS”判断△ABC≌△DCB．
故选：A．
【点评】本题考查了全等三角形的判定：熟练掌握全等三角形的5种判定方法是解决问题的关键．选用哪一种判定方法，取决于题目中的已知条件．
16．（2021秋•越城区期末）△ABC与三边长分别为3，4，5的三角形全等，满足条件的△ABC的边角可以是（ ）
A．∠A＝90°，AB＝3，BC＝5B．∠B＝90°，AB＝5，BC＝3
C．∠C＝90°，AC＝3，AB＝4D．∠C＝90°，AB＝4，BC＝3
【分析】首先根据勾股定理的逆定理判定三边长分别为3，4，5的三角形是直角三角形，再根据直角三角形的判定方法判定即可．
【解答】解：∵32+42＝52，
∴三边长分别为3，4，5的三角形是直角三角形，且斜边为5．
∵△ABC与三边长分别为3，4，5的三角形全等，
∴满足条件的△ABC的边角可以是∠A＝90°，AB＝3，BC＝5；或∠B＝90°，AC＝5，BC＝3；或∠C＝90°，AC＝3，AB＝5；或∠C＝90°，AB＝5，BC＝3．
故选：A．
【点评】本题重点考查了三角形全等的判定定理，普通两个三角形全等共有四个定理，即AAS、ASA、SAS、SSS，直角三角形可用HL定理．也考查了勾股定理的逆定理．
17．（2021秋•柯桥区期末）如图，已知AB＝AD，AC＝AE，若要判定△ABC≌△ADE，则下列添加的条件中正确的是（ ）
A．∠1＝∠DACB．∠B＝∠DC．∠1＝∠2D．∠C＝∠E
【分析】已知两边，若要证明△ABC≌△ADE，只需添加夹角，由此可求解．
【解答】解：A．当∠1＝∠DAC时，∠BAC＝2∠1不一定等于∠EAD，
∴不能判断△ABC≌△ADE，
故A不正确；
B．当∠B＝∠D时，
∵AB＝AD，AC＝AE，
∴已知两边对应相等，一个角对应相等，但∠B＝∠D不是夹角，
∴不能判断△ABC≌△ADE，
故B不正确；
C．∵∠BAC＝∠1+∠DAC，∠CAD＝∠2+∠DAC，
若∠BAC＝∠CAD，则∠1＝∠2，
∵AB＝AD，∠BAC＝∠CAD，AC＝AE，
∴△ABC≌△ADE（SAS），
故C正确；
D．当∠C＝∠E时，
∵AB＝AD，AC＝AE，
∴已知两边对应相等，一个角对应相等，但∠C＝∠E不是夹角，
∴不能判断△ABC≌△ADE，
故D不正确；
故选：C．
【点评】本题考查三角形全等的判定，熟练掌握三角形全等的判定方法是解题的关键．
18．（2021秋•普陀区期末）如图，AB＝AC，请你添加一个条件，使△ABE≌△ACD，
（1）你添加的条件是 AD＝AE或∠B＝∠C（答案不唯一） ；
（2）根据上述添加的条件证明△ABE≌△ACD．
【分析】（1）根据全等三角形的判定定理即可得出结论；
（2）若添加∠B＝∠C，根据ASA定理即可得出结论．
【解答】解：（1）添加的条件是∠B＝∠C或AE＝AD．
故答案为：AD＝AE或∠B＝∠C（答案不唯一）；

（2）若添加∠B＝∠C，
在△ABE和△ACD中
∵，
∴△ACD≌△ABE（ASA）．
【点评】此题主要考查了全等三角形的判定，关键是掌握判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．
19．（2021秋•温州期中）看图填空：
已知：如图，BC∥EF，AD＝BE，BC＝EF，试说明△ABC≌△DEF．
解：∵BC∥EF
∴∠ABC＝∠ E （两直线平行，同位角相等）
∵AD＝BE
∴ AD+DB ＝BE+DB
即 AB ＝DE
在△ABC和△DEF中
∴△ABC≌△DEF（ SAS ）
【分析】根据线段的和差求出AB＝DE，根据平行线的性质得出∠ABC＝∠E，根据全等三角形的判定定理推出即可．
【解答】解：∵BC∥EF，
∴∠ABC＝∠E（两直线平行，同位角相等），
∵AD＝BE，
∴AD+DB＝BE+DB，
即：AB＝DE，
在△ABC和△DEF中，
，
∴△ABC≌△DEF（SAS），
故答案为：E；AD+DB；AB；SAS．
【点评】此题考查了全等三角形的判定，熟记全等三角形的判定定理是解题的关键．
20．（2021秋•仙桃校级月考）如图，点C在线段BD上，AB⊥BD于B，ED⊥BD于D．∠ACE＝90°，且AC＝5cm，CE＝6cm，点P以2cm/s的速度沿A→C→E向终点E运动，同时点Q以3cm/s的速度从E开始，在线段EC上往返运动（即沿E→C→E→C→…运动），当点P到达终点时，P，Q同时停止运动．过P，Q分别作BD的垂线，垂足为M，N．设运动时间为ts，当以P，C，M为顶点的三角形与△QCN全等时，求t的值．
【分析】分三种情况讨论，由全等三角形的判定和性质可求解．
【解答】解：当点P在AC上，点Q在CE上时，
∵以P，C，M为顶点的三角形与△QCN全等，
∴PC＝CQ，
∴5﹣2t＝6﹣3t，
∴t＝1，
当点P在AC上，点Q第一次从点C返回时，
∵以P，C，M为顶点的三角形与△QCN全等，
∴PC＝CQ，
∴5﹣2t＝3t﹣6，
∴t＝，
当点P在CE上，点Q第一次从E点返回时，
∵以P，C，M为顶点的三角形与△QCN全等，
∴PC＝CQ，
∴2t﹣5＝18﹣3t，
∴t＝，
综上所述：t的值为1或或．
【点评】本题考查了全等三角形的判定，掌握全等三角形的判定和用分类讨论的思想解决问题是本题的关键．
四．全等三角形的判定与性质（共9小题）
21．（2021秋•龙泉市期末）如图，点D，E分别在AC，AB上，AD＝AE，BE＝CD．
（1）求证：BD＝CE．
（2）若∠A＝55°，∠C＝30°，求∠COD的度数．
【分析】（1）根据等式的性质得AB＝AC，再利用SAS证明△ABD≌△ACE即可；
（2）由三角形内角和定理得∠AEC的度数，再由△ABD≌△ACE，得∠ADB＝∠AEC＝95°，最后运用三角形外角的性质可得答案．
【解答】（1）证明：∵AD＝AE，BE＝CD，
∴AB＝AC，
在△ABD与△ACE中，
，
∴△ABD≌△ACE（SAS），
∴BD＝CE；
（2）解：∵∠A＝55°，∠C＝30°，
∴∠AEC＝180°﹣55°﹣30°＝95°，
∵△ABD≌△ACE，
∴∠ADB＝∠AEC＝95°，
∴∠COD＝∠ADB﹣∠C＝95°﹣30°＝65°．
【点评】本题主要考查了全等三角形的判定与性质，三角形内角和定理等知识，证明△ABD≌△ACE是解题的关键．
22．（2021秋•瑞安市校级期中）如图，点A，F，C，D在同一条直线上，AF＝DC，AB＝DE，∠A＝∠D，BC与EF交于点H．
求证：（1）△ABC≌△DEF；
（2）FH＝CH．
【分析】（1）利用ASA即可证明△ABC≌△DEF；
（2）根据△ABC≌△DEF，可得∠ACB＝∠EFD，再根据等角对等边即可解决问题．
【解答】证明：（1）∵AF＝CD，
∴AC＝DF，
在△ABC和△DEF中，
，
∴△ABC≌△DEF（ASA）；
（2）∵△ABC≌△DEF，
∴∠ACB＝∠EFD，
∴FH＝CH．
【点评】本题考查全等三角形的判定和性质、平行线的性质等知识，熟练掌握全等三角形的判定方法是解决问题的关键．
23．（2021春•镇海区校级期末）如图，在△ABC中，BD平分∠ABC，∠C＝2∠CDB，AB＝12，CD＝3，则△ABC的周长为（ ）
A．21B．24C．27D．30
【分析】在AB上截取BE＝BC，由“SAS”可证△CBD≌△EBD，可得∠CDB＝∠BDE，∠C＝∠DEB，可证∠ADE＝∠AED，可得AD＝AE，即可求解．
【解答】解：如图，在AB上截取BE＝BC，连接DE，
∵BD平分∠ABC，
∴∠ABD＝∠CBD，
在△CBD和△EBD中，
，
∴△CBD≌△EBD（SAS），
∴∠CDB＝∠BDE，∠C＝∠DEB，
∵∠C＝2∠CDB，
∴∠CDE＝∠DEB，
∴∠ADE＝∠AED，
∴AD＝AE，
∴△ABC的周长＝AD+AE+BE+BC+CD＝AB+AB+CD＝27，
故选：C．
【点评】本题考查了全等三角形的判定和性质，等腰三角形的性质，添加恰当辅助线构造全等三角形是解题的关键．
24．（2021秋•开化县期末）如图，在△ABC中，AB＝AC，点D，E在BC上，BD＝CE．
（1）求证：△ABD≌△ACE．
（2）若∠DAE＝∠B＝28°，求∠BAD的度数．
【分析】（1）由AB＝AC得∠B＝∠C，还有条件BD＝CE，即可根据“SAS”证明△ABD≌△ACE；
（2）由△ABD≌△ACE得AD＝AE，而∠DAE＝28°，则∠ADE＝∠AED＝76°，再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BAD的度数．
【解答】（1）证明：如图，∵AB＝AC，
∴∠B＝∠C，
在△ABD和△ACE中，
∴，
∴△ABD≌△ACE（SAS），
（2）解：∵AD＝AE，∠DAE＝28°，
∴∠ADE＝∠AED＝×（180°﹣28°）＝76°，
∵∠ADE＝∠BAD+∠B，且∠B＝28°，
∴∠BAD＝∠ADE﹣∠B＝76°﹣28°＝48°，
∴∠BAD的度数48°．
【点评】此题考查等腰三角形的性质、全等三角形的判定与性质、三角形内角和定理及其推论等知识，证明△ABD≌△ACE是解题的关键．
25．（2021秋•椒江区期末）如图，点A，D在线段FC上，FA＝CD，AB＝DE，BC＝EF．求证：AB∥DE．
【分析】由“SSS”可证△ABC≌△DEF，可得∠BAC＝∠EDF，可得结论．
【解答】证明：∵FA＝CD，
∴FD＝AC，
在△ABC和△DEF中，
，
∴△ABC≌△DEF（SSS），
∴∠BAC＝∠EDF，
∴AB∥DE．
【点评】本题考查了全等三角形的判定和性质，证明三角形全等是解题的关键．
26．（2021秋•滨江区校级期中）如图，∠BAD＝90°，AC平分∠BAD，CB＝CD，则∠B与∠ADC满足的数量关系为（ ）
A．∠B＝∠ADCB．2∠B＝∠ADC
C．∠B+∠ADC＝180°D．∠B+∠ADC＝90°
【分析】在射线AD上截取AE＝AB，连接CE，根据SAS不难证得△ABC≌△AEC，从而得BC＝EC，∠B＝∠AEC，可求得CD＝CE，得∠CDE＝∠CED，证得∠B＝∠CDE，即可得出结果．
【解答】解：在射线AD上截取AE＝AB，连接CE，如图所示：
∵∠BAD＝90°，AC平分∠BAD，
∴∠BAC＝∠EAC，
在△ABC与△AEC中，
，
∴△ABC≌△AEC（SAS），
∴BC＝EC，∠B＝∠AEC，
∵CB＝CD，
∴CD＝CE，
∴∠CDE＝∠CED，
∴∠B＝∠CDE，
∵∠ADC+∠CDE＝180°，
∴∠ADC+∠B＝180°．
故选：C．
【点评】本题主要考查全等三角形的判定与性质，解答的关键是作出适当的辅助线AE，CE．
27．（2021秋•诸暨市月考）如图，在△ABC与△AEF中，AB＝AE，BC＝EF，∠ABC＝∠AEF，∠EAB＝40°，AB交EF于点D，连接EB．下列结论：①∠FAC＝40°；②AF＝AC；③∠EBC＝110°；④AD＝AC；⑤∠EFB＝40°，正确的个数为（ ）个．
A．1B．2C．3D．4
【分析】证明△AEF≌△ABC（SAS），利用全等三角形的性质，可以推出①②⑤正确，利用反证法推出③④错误即可．
【解答】解：在△AEF和△ABC中，
，
∴△AEF≌△ABC（SAS），
∴∠EAF＝∠BAC，AF＝AC，故②正确
∴∠EAB＝∠FAC＝40°，故①正确，
∴∠C＝∠AFC＝∠AFE＝70°，
∴∠EFB＝180°﹣70°﹣70°＝40°，故⑤正确，
∵AE＝AB，∠EAB＝40°，
∴∠AEB＝∠ABE＝70°，
若∠EBC＝110°，则∠ABC＝40°＝∠EAB，
∴∠EAB＝∠ABC，
∴AE∥BC，显然与题目条件不符，故③错误，
若AD＝AC，则∠ADF＝∠AFD＝70°，
∴∠DAF＝40°，这个显然与条件不符，故④错误．
故选：C．
【点评】本题考查全等三角形的判定和性质，等腰三角形的判定和性质，三角形内角和定理等知识，解题的关键是证明△AEF≌△ABC．
28．（2021秋•高邑县期末）如图，AB⊥CD，且AB＝CD，E，F是AD上两点，CE⊥AD，BF⊥AD．若CE＝4，BF＝3，EF＝2，则AD的长为（ ）
A．3B．5C．6D．7
【分析】只要证明△ABF≌△CDE，可得AF＝CE＝4，BF＝DE＝3，推出AD＝AF+DF＝4+（3﹣2）＝5；
【解答】解：∵AB⊥CD，CE⊥AD，BF⊥AD，
∴∠AFB＝∠CED＝90°，∠A+∠D＝90°，∠C+∠D＝90°，
∴∠A＝∠C，∵AB＝CD，
∴△ABF≌△CDE（AAS），
∴AF＝CE＝4，BF＝DE＝3，
∵EF＝2，
∴AD＝AF+DF＝4+（3﹣2）＝5，
故选：B．
【点评】本题考查全等三角形的判定和性质，解题的关键是正确寻找全等三角形解决问题，属于中考常考题型．
29．（2021秋•柯桥区期末）如图，在△ABC中，∠ABC＝45°，CD⊥AB，BE⊥AC，CD与BE相交于点F．
（1）求证：△ACD≌△FBD；
（2）若AD＝3，BF＝5，求△ABC的面积．
【分析】（1）由“ASA”可证△ACD≌△FBD；
（2）由全等三角形的性质可得AC＝BF＝5，由勾股定理可求出CD，最后根据三角形面积公式得解．
【解答】（1）证明：∵CD⊥AB，BE⊥AC，
∴∠ADC＝∠FDB＝90°，
∴∠A+∠DBF＝∠A+∠ACD＝90°，
即∠DBF＝∠ACD，
∵∠ABC＝45°，
∴∠BCD＝∠ABC＝45°，
∴DB＝DC，
在△ACD和△FBD中，
，
∴△ACD≌△FBD（ASA）；
（2）∵△ACD≌△FBD，
∴AD＝DF＝3，
在Rt△BDF中，BD＝4，
∴CD＝4，AB＝7，
∴S△ABC＝4×7÷2＝14．
【点评】本题考查了全等三角形的判定和性质，勾股定理，等腰直角三角形的性质，证明三角形全等是解题的关键．
五．全等三角形的应用（共6小题）
30．（2021秋•肇源县期末）王强同学用10块高度都是2cm的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚好可以放进一个等腰直角三角板（AC＝BC，∠ACB＝90°），点C在DE上，点A和B分别与木墙的顶端重合．
（1）求证：△ADC≌△CEB；
（2）求两堵木墙之间的距离．
【分析】（1）根据题意可得AC＝BC，∠ACB＝90°，AD⊥DE，BE⊥DE，进而得到∠ADC＝∠CEB＝90°，再根据等角的余角相等可得∠BCE＝∠DAC，再证明△ADC≌△CEB即可；
（2）利用全等三角形的性质进行解答．
【解答】（1）证明：由题意得：AC＝BC，∠ACB＝90°，AD⊥DE，BE⊥DE，
∴∠ADC＝∠CEB＝90°，
∴∠ACD+∠BCE＝90°，∠ACD+∠DAC＝90°，
∴∠BCE＝∠DAC
在△ADC和△CEB中，
∴△ADC≌△CEB（AAS）；
（2）解：由题意得：AD＝2×3＝6（cm），BE＝7×2＝14（cm），
∵△ADC≌△CEB，
∴EC＝AD＝6cm，DC＝BE＝14cm，
∴DE＝DC+CE＝20（cm），
答：两堵木墙之间的距离为20cm．
【点评】此题主要考查了全等三角形的应用，关键是正确找出证明三角形全等的条件．
31．（2021秋•临海市期末）如图，有两个长度相同的滑梯靠在一面墙上．已知左边滑梯的高度AC与右边滑梯的水平长度DF相等，那么判定△ABC与△DEF全等的依据是（ ）
A．HLB．ASAC．AASD．SSS
【分析】先根据BC＝EF，AC＝DF判断出Rt△ABC≌Rt△DEF．
【解答】解：∵滑梯、墙、地面正好构成直角三角形，
在Rt△ABC和Rt△DEF中，
，
∴Rt△ABC≌Rt△DEF（HL），
故选：A．
【点评】本题考查的是全等三角形的判定及性质，直角三角形的性质，属较简单题目．
32．（2021秋•椒江区期末）小明在学习了全等三角形的相关知识后，发现了一种测量距离的方法，如图，小明直立在河岸边的O处，他压低帽子帽沿，使视线通过帽沿，恰好落在河对岸的A处，然后转过身，保持和刚才完全一样的姿势，这时视线落在水平地面的B处（A，O，B三点在同一水平直线上），小明通过测量O，B之间的距离，即得到O，A之间的距离．小明这种方法的原理是（ ）
A．SSSB．SASC．ASAD．HL
【分析】根据垂直的定义和全等三角形的判定和性质定理即可得到结论．
【解答】解：∵AB⊥CO，
∴∠ACO＝∠BCO，
在△AOC与△BOC中，
，
∴△AOC≌△BOC（ASA），
∴AO＝BO，
故选：C．
【点评】本题考查了全等三角形的应用，熟练掌握全等三角形的判定和性质定理是解题的关键．
33．（2021秋•慈溪市期末）如图，为测量池塘两端AB的距离，学校课外实践小组在池塘旁的开阔地上选了一点C，测得∠ACB的度数，在AC的另一侧测得∠ACD＝∠ACB，CD＝CB，再测得AD的长，就是AB的长．其依据是（ ）
A．SSSB．SASC．ASAD．AAS
【分析】已知条件是∠ACD＝∠ACB，CD＝CB，AC＝AC，据此作出选择．
【解答】解：在△ABC与△ADC中，
．
∴△ABC≌△ADC（SAS）．
故选：B．
【点评】此题考查了全等三角形的应用，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS，做题时注意选择．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．
34．（2021秋•金华期中）如图，一块玻璃碎成三片，小智只带了第③块去玻璃店，就能配一块一模一样的玻璃，你能用三角形的知识解释，这是为什么？（ ）
A．ASAB．AASC．SASD．SSS
【分析】根据全等三角形的判定，已知两角和夹边，就可以确定一个三角形．
【解答】解：根据三角形全等的判定方法，根据角边角可确定一个全等三角形，
只有第三块玻璃包括了两角和它们的夹边，只有带③去才能配一块完全一样的玻璃，是符合题意的．
故选：A．
【点评】本题考查三角形全等的判定方法，熟练掌握判定两个三角形全等的方法：SSS、SAS、ASA、AAS是解决问题的关键．
35．（2021秋•金华期末）如图，A，B两点分别位于一个池塘的两端，小明通过构造△ABC与△BCD来测量A，B间的距离，其中AC＝CD，∠ACB＝∠BCD．那么量出的BD的长度就是AB的距离．请你判断小明这个方法正确与否，并给出相应理由．
【分析】正确；利用全等三角形的判定定理SAS证得△ABC≌△DBC，由该全等三角形的对应边相等得到AB＝DB．
【解答】解：正确；理由如下：
在△ABC与△DBC中，
．
∴△ABC≌△DBC（SAS）．
∴AB＝DB．
【点评】本题考查全等三角形的应用．在实际生活中，对于难以实地测量的线段，常常通过两个全等三角形，转化需要测量的线段到易测量的边上或者已知边上来，从而求解．
一、单选题
1．（2021·土默特左旗教育局教研室八年级月考）如图，已知，，欲证，不可补充的条件是（ ）
A．B．C．D．
【答案】D
【分析】根据全等三角形的判定方法，逐项判断即可．
【详解】解：∵，，
A、若，可利用SSS证明，故本选项不符合题意；
B、若，可得 ，可利用SAS证明，故本选项不符合题意；
C、若，可利用SAS证明，故本选项不符合题意；
D、若，不能证明，故本选项符合题意；
故选：D．
【点睛】本题主要考查了全等三角形的判定，熟练掌握全等三角形的判定方法——SAS、ASA、AAS、SSS是解题的关键．
2．（2021·全国八年级课前预习）如图，△ABC≌△BAD，如果AB＝6cm，BD＝4cm，AD＝5cm，那么BC的长是（ ）
A．6cmB．5cmC．4cmD．无法确定
【答案】B
3．（2021·通道侗族自治县教育科学研究室八年级期中）下列条件中，不能使两个直角三角形全等的条件是
A．一锐角和斜边对应相等B．斜边和一直角边对应相等
C．有三条边对应相等D．两个锐角对应相等
【答案】D
【分析】要判断能使两个直角三角形全等的条件首先要看现在有的条件：一对直角对应相等，还需要两个条件，而三个角相等是不能判定三角形全等的，所以符合题意的答案只有选项D了．
【详解】A、一锐角和斜边对应相等，利用已知的直角相等，能通过两角及其一角的对边对应相等判定两个直角三角形全等，故本选项不符合题意；
B、斜边和一条直角边对应相等，利用已知的直角相等，能通过直角三角形斜边和一条直角对应相等判定两个直角三角形全等，故本选项不符合题意；
C、有三条边对应相等，能通过三边对应相等判定两个直角三角形全等，故本选项不符合题意；
D、两个锐角对应相等时，由三个角相等不能判定两个直角三角形全等，故本选项符合题意．
故选：D．
【点睛】本题考查的是直角三角形的判定方法，属于基础题，熟练掌握全等三角形的判定定理是解题的关键．
4．（2021·通道侗族自治县教育科学研究室八年级期中）在中，，的平分线交于D，若，则点D到的距离是
A．B．C．D．
【答案】B
【分析】根据角平分线上的点到角的两边距离相等可得DE=CD，再根据点到线段的距离的定义解答．
【详解】解：如下图，过点D作DE⊥AB于E，
∵∠C=90°，BD是∠ABC的平分线，
∴DE=CD，
∵CD=4cm，
∴DE=4cm，
∴点D到AB的距离DE是4cm．
故选：B．
【点睛】本题考查了角平分线上的点到角的两边距离相等的性质，点到线段的距离的定义，熟记性质与概念是解题的关键．
5．（2020·南京市金陵汇文学校八年级开学考试）下列各条件中，不能作出唯一三角形的是（ ）
A．已知两边和夹角
B．已知两角和夹边
C．已知两边和其中一边的对角
D．已知三边
【答案】C
【分析】根据全等三角形的判定知识得到不能作出唯一三角形的选项即可．
【详解】解：A、根据可得能作出唯一三角形；
B、根据可得能作出唯一三角形；
C、根据SSA不能做出唯一三角形；
D、根据可得能作出唯一三角形.
故选C．
【点睛】主要考查全等三角形的判定的应用；注意不能判定两三角形全等，也不能作出唯一的三角形．
6．（2021·河北秦皇岛市·八年级期中）如图，在方格纸中，以为一边作，使之与全等，从，，，四个点中找出符合条件的点，则点有（ ）
A．个B．个C．个D．个
【答案】C
【分析】根据全等三角形的判定得出点P的位置即可．
【详解】解：要使△ABP与△ABC全等，点P到AB的距离应该等于点C到AB的距离，即3个单位长度，故点P的位置可以是P1，P3，P4三个，
故选：C．
【点睛】此题考查全等三角形的判定，关键是利用全等三角形的判定进行判定点P的位置．
7．（2021·全国八年级专题练习）如图，点在同一直线上，，则等于（ ）
A．4B．5C．6D．7
【答案】A
【分析】根据全等三角形的性质得出AC=DF，即可得出选项．
【详解】解：∵△ABC≌△DEF，DF=4，
∴AC=DF=4，
故选：A．
【点睛】本题考查了全等三角形的性质，能熟记全等三角形的性质的内容是解此题的关键，注意：全等三角形的对应边相等，对应角相等．
8．（2021·大连市第三十四中学八年级月考）如图，，，则的度数为（ ）
A．B．C．D．
【答案】A
【分析】根据全等三角形的性质，结合已知条件和角度的计算即可求得．
【详解】，
，
即，
，
，
．
故选A．
【点睛】本题考查了全等三角形的性质，掌握全等三角形的性质是解题的关键．
9．（2021·大连市第三十四中学八年级月考）如图，，其中，，则（ ）
A．B．C．D．
【答案】B
【分析】利用全等三角形的性质，三角形内角和定理计算即可．
【详解】∵，∠A=36°，=24°，
∴∠C==24°，
∴∠B=180°-∠A-∠C=180°-36°-24°=120°，
故选B．
【点睛】本题考查了全等三角形的性质，三角形内角和定理，熟练掌握性质，灵活运用内角和定理是解题的关键．
10．（2020·南京市金陵汇文学校八年级开学考试）下列命题中正确的是（ ）
A．全等三角形的高相等
B．全等三角形的中线相等
C．全等三角形的角平分线相等
D．全等三角形的对应角平分线相等
【答案】D
【分析】根据全等三角形的性质对A、B、C、D进行判断．
【详解】解：A、全等三角形的对应边的高相等，故此选项错误；
B、全等三角形的对应边的中线相等，故此选项错误；
C、全等三角形的对应角平分线相等，故此选项错误；
D、全等三角形的对应角平分线相等，故此选项正确.
故选D．
【点睛】本题考查全等三角形的性质，解题的关键是熟练掌握基本知识，属于中考常考题型．
二、填空题
11．（2021·宁夏八年级期末）如图，△ABC≌△DBC，∠A＝45°，∠DCB＝43°，则∠ABC＝______．
【答案】92°
【分析】根据全等三角形的性质和三角形的内角和定理即可得到结论．
【详解】解：∵△ABC≌△DBC，
∴∠ACB＝∠DCB＝43°，
∵∠A＝45°，
∴∠ABC＝180°﹣∠A﹣∠ACB＝92°，
故答案为：92°．
【点睛】本题考查了三角形内角和定理，全等三角形的性质，能正确运用全等三角形的性质进行推理是解此题的关键，注意：全等三角形的对应边相等，对应角相等．
12．（2021·全国八年级课前预习）如图，长方形ABCD沿AM折叠，使D点落在BC上的N点处，AD＝7cm，DM＝5cm，∠DAM＝39°，则△ANM≌△ADM，AN＝_____cm，NM＝_____cm，∠NAB＝_______．
【答案】7 5 12°
13．（2021·全国八年级课前预习）能够完全重合的两个三角形叫做_______．
【答案】全等三角形
14．（2021·河北唐山市·八年级期中）已知：如图，AE⊥AB，且AE＝AB，BC⊥CD且BC＝CD，根据图中所标注的数据，可求得阴影部分的面积为_______．
【答案】50
【分析】由AE⊥AB，EF⊥FH，BG⊥AG，可以得到∠EAF＝∠ABG，而AE＝AB，∠EFA＝∠AGB，由此可以证明△EFA≌△ABG，所以AF＝BG，AG＝EF，同理证得△BGC≌△DHC，GC＝DH，CH＝BG．故FH＝FA+AG+GC+CH＝3+6+4+3＝16，然后利用面积的割补法和面积公式即可求出图形的面积．
【详解】解：∵AE⊥AB且AE＝AB，EF⊥FH，BG⊥FH，
∴∠EAB＝∠EFA＝∠BGA＝90°，
∵∠EAF+∠BAG＝90°，∠ABG+∠BAG＝90°，
∴∠EAF＝∠ABG，
∴AE＝AB，∠EFA＝∠AGB，∠EAF＝∠ABG，
∴△EFA≌△ABG（AAS），
∴AF＝BG，AG＝EF
同理证得：△BGC≌△DHC（AAS），得GC＝DH，CH＝BG
故FH＝FA+AG+GC+CH＝3+6+4+3＝16，
故，
即：S(6+4）×16﹣3×4﹣6×3＝50．
故答案为：50．
【点睛】此题考查了全等三角形的判定与性质、等腰直角三角形的性质，熟练掌握相关基本性质是解题的关键．
15．（2021·嵩县教育局基础教育教学研究室八年级期末）如图，已知，和，，则度数为__________．
【答案】
【分析】先证明 ，可得 ，再根据三角形外角的性质，即可求解．
【详解】解：∵，， ，
∴ ，
∴，
∵，
∴ ，
∵，
∴．
故答案为： ．
【点睛】本题主要考查了全等三角形的判定和性质，三角形的外角性质，熟练掌握全等三角形的判定定理和性质定理是解题的关键．
16．（2021·广南县教学研究室八年级期末）如图，在中，，AD是的一条角平分线．若，则点D到AB的距离为___________．
【答案】6
【分析】根据角平分线上的点到角的两边的距离相等的性质可得点D到AB的距离DE长为等于CD的长，进行解答即可．
【详解】解：过D作DE⊥AB，
∵AD是∠BAC的角平分线，∠C＝90°，
∴DE＝CD，
∵CD＝6，
∴DE＝6，
∴点D到AB的距离为6
故答案为：6．
【点睛】本题主要考查了角平分线上的点到角的两边的距离相等的性质，是基础题，比较简单．
17．（2021·北京市第五中学朝阳双合分校八年级期中）如图，把两根钢条的中点连在一起，可以做成一个测量工件内槽宽的工具（卡钳），在图中，要测量工件内槽宽AB，只要测量A'B'的长度即可，该做法的依据是 ___．
【答案】根据证明．
【分析】根据测量两点之间的距离，只要符合全等三角形全等的条件之一，只需要测量易测量的边上，进而得出答案．
【详解】解：连接，，如图，
点分别是、的中点，
，，
在和中，
，
∴．
．
答：需要测量的长度，即为工件内槽宽．
其依据是根据证明；
故答案为：根据证明．
【点睛】本题考查全等三角形的应用，根据已知条件可用边角边定理判断出全等．
18．（2021·全国八年级单元测试）已知△ADF≌△CBE，∠A=20°，∠B=120°，则∠CEB= ______．
【答案】40°
【分析】先根据经全等三角形的性质求出∠C=∠A=20°，再根据三角形内角和求解．
【详解】解：∵△ADF≌△CBE，
∴∠C=∠A=20°，
∵∠B=120°，
∴∠CEB=180°-∠C-∠B=180°-20°-120°=40°，
故答案为：40°．
【点睛】本题考查了全等三角形的性质，三角形的内角和，熟练掌握全等三角形的对应角相等是解答本题的关键．
19．（2020·南京市金陵汇文学校八年级开学考试）如图，已知∠B=∠DEF，AB=DE，要证明△ABC≌△DEF．
（1）若以“ASA”为依据，还需要添加一个条件为___________；
（2）若以“AAS”为依据，还需要添加一个条件为___________．
【答案】∠A=∠D ∠ACB=∠DFE
【分析】（1）根据边角边的条件先找到对应边，再写出条件，最后给出证明；
（2）根据角角边的条件先找到角，再写出条件，最后写理由.
【详解】解：（1），要使，且以“SAS”为依据，
∴还要添加的条件为：；
在和中
∴（ASA）
故答案为；
（2），要使，且以“”为依据，
∴还要添加的条件为：．
在和中
∴（AAS）
故答案为．
【点睛】此题重点考查学生对三角形全等的条件的理解，掌握三角形全等的判定方法是解题的关键.
20．（2021·全国八年级单元测试）如图，在△ABC中，AB＝AC＝24厘米，∠B=∠C ，BC＝16厘米，点D为AB的中点，点P在线段BC上以4厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．当点Q的运动速度为________厘米/秒时，能够在某一时刻使△BPD与△CQP全等．
【答案】4或6
【分析】设点Q的速度为x，则运动t秒时，CQ=xt，分两种情况讨论①当△BPD≌△CQP时，②当△BPD≌△CPQ时，根据其运动情况表示出线段的数量关系，根据三角形全等的性质计算得到答案即可．
【详解】解：设点Q的速度为x，则运动t秒时，CQ=xt，
∵P点的速度为4，BC=16
∴BP=4t，PC=（16-4t）
又∵AB=AC=24，点D为AB的中点
∴BD=AB=12
∵∠B=∠C
∴运动t秒时，△BPD与△CQP全等共有两种情况
①当△BPD≌△CQP时，
则有BD=CP，BP=CQ
即12=16-4t，4t=xt
即t=1
∴由4t=xt可知，x=4．
②当△BPD≌△CPQ时，
则有BD=CQ，BP=CP
即12=xt，4t=16-4t
∴t=2，x=6．
综合①②可知速度为4或6．
故答案为：4或6．
【点睛】本题考查了三角形全等的性质，分类讨论是解题的关键．
三、解答题
21．（2021·山东日照市·海曲中学八年级期中）如图所示，ABCD中，AE⊥BD，,垂足分别为E，F．求证：AE＝CF．
【分析】根据平行四边形的性质得出AB＝CD，AB∥CD，根据平行线的性质得出∠ABE＝∠CDF，求出∠AEB＝∠CFD＝90°，根据AAS推出△ABE≌△CDF即可．
【详解】证明：∵四边形ABCD是平行四边形，
∴AB＝CD，AB∥CD，
∴∠ABE＝∠CDF，
∵AE⊥BD，CF⊥BD，
∴∠AEB＝∠CFD＝90°，
在△ABE和△CDF中，
，
∴△ABE≌△CDF（AAS），
∴AE＝CF．
【点睛】本题考查了平行四边形的性质，平行线的性质，全等三角形的性质和判定的应用，解此题的关键是求出△ABE≌△CDF，注意：平行四边形的对边平行且相等，难度适中．
22．（2021·全国八年级课前预习）如图△ABC与△ADC全等，请用数学符号表示出这两个三角形全等，并写出相等的边和角．
【详解】△ABC≌△ADC，
相等的边：AB＝AD，AC＝AC，BC＝DC
相等的角：∠BCA＝∠DAC，∠B＝∠D，∠ACB＝∠ACD
23．（2021·吉林长春市·长春外国语学校八年级开学考试）如图，△ABC ≌△DEF，点A对应点D，点B对应点E，点B、F、C、E在一条直线上，∠A = 85°，∠E = 50°，AB = 4，EF = 6．
（1）求∠ACB的度数．
（2）求AC边的取值范围．
【答案】（1）45°；（2）2＜AC＜10
【分析】（1）根据全等三角形的性质求出∠B，再利用三角形内角和求解；
（2）根据全等三角形的性质求出BC，再根据三角形的三边关系求解即可．
【详解】解：（1）∵△ABC ≌△DEF，
∴∠B=∠E=50°，
∵∠A=85°，
∴∠ACB=180°-∠B-∠A=45°；
（2）∵△ABC ≌△DEF，
∴BC=EF=6，
∵AB=4，
∴AC的范围是2＜AC＜10．
【点睛】本题考查了全等三角形的性质，三角形的三边关系，三角形内角和定理，解题的关键是利用全等三角形得到相等边和角．
24．（2021·湖南八年级期末）已知：如图，，且，，，四点在一条直线上，，，，．
（1）求的度数与的长；
（2）求证：．
【答案】（1），；（2）见解析
【分析】（1）根据三角形内角和定理求得∠ACB，根据全等三角形的性质可得，，即可求解；
（2）根据全等三角形的性质可得，继而根据平行线的判定求证结论．
【详解】解：（1）∵，，
∴．
∵，
∴，
，
∵，，
∴．
（2）证明：∵，
∴，
∴．
【点睛】本题考查全等三角形的判定和性质，三角形内角和定理、平行线的判定，解题的关键是熟练运用全等三角形的性质．
25．（2021·北京市第五中学朝阳双合分校八年级期中）根据题意，先在图中作出辅助线，再完成下列填空：如图，△ABC中，AD平分∠BAC，DE所在直线是BC的垂直平分线，点E为垂足，过点D作DM⊥AB于M，DN⊥AC交AC的延长线于N，求证：BM＝CN．
证明：连接DB，DC
∵AD平分∠BAC，DM⊥AB，DN⊥AN
∴DM＝① （② ）
∵DE是BC的垂直平分线
∴DB＝③ （④ ）
在⑤ 和⑥ 中
∴⑦ ≌⑧ （⑨ ）
∴BM＝CN（⑩ ）
【答案】①DN；②角平分线上的点到角两边的距离相等；③DC；④线段垂直平分线上的点与这条线段两个端点的距离相等；⑤Rt△BDM；⑥Rt△CDN；⑦Rt△BDM；⑧Rt△BDM；⑨HL；⑩全等三角形的对应边相等．
【分析】连接BD，DC，利用线段垂直平分线的性质得出BD＝CD，利用角平分线的性质得出DM＝DN，进而证明△BMD与△CDN全等即可．
【详解】证明：（1）连接BD，如图：
证明：连接DB，DC，
∵AD平分∠BAC，DM⊥AB，DN⊥AN，
∴DM＝DN（角平分线上的点到角两边的距离相等），
∵DE是BC的垂直平分线，
∴DB＝CD（线段垂直平分线上的点与这条线段两个端点的距离相等），
在Rt△BDM和Rt△CDN中，
∴Rt△BDM≌Rt△BDM（HL），
∴BM＝CN（全等三角形的对应边相等），
故答案为：①DN；②角平分线上的点到角两边的距离相等；
③DC；④线段垂直平分线上的点与这条线段两个端点的距离相等；
⑤Rt△BDM；⑥Rt△CDN；⑦Rt△BDM；⑧Rt△BDM；⑨HL；
⑩全等三角形的对应边相等．
【点睛】此题考查全等三角形的判定和性质，关键是证明△BDM与△CDN全等．
26．（2021·浙江八年级期末）如图，已知正方形边长为，动点M从点C出发，沿着射线的方向运动，动点P从点B出发，沿着射线的方向运动，连结，
（1）若动点M和P都以每秒的速度运动，问t为何值时和全等？
（2）若动点P的速度是每秒，动点M的速度是每秒问t为何值时和全等？
【答案】（1）t=1；（2）t=或t=
【分析】（1）根据△DCP与△BCM全等，列出关于t的方程，解之即可；
（2）分当点P在点C左侧和当点P在点C右侧，两种情况，根据PC=CM，列方程求解即可．
【详解】解：（1）要使△DCP与△BCM全等，
则PC=CM，
由题意得：2t=4-2t，
解得：t=1；
（2）当点P在点C左侧时，
则△DCP≌△BCM，
∴PC=CM，
∴4-3t=1.5t，
解得：t=；
当点P在点C右侧时，
则△DCP≌△BCM，
∴CP=CM，
∴3t-4=1.5t，
解得：t=，
综上：当t=或t=时，△DCP与△BCM全等．
【点睛】本题考查了全等三角形的判定和性质，解题的关键是抓住全等三角形的条件，得到相等线段，列出方程，注意分类讨论．
27．（2021·广南县教学研究室八年级期末）在中，，，点D为直线BC上的一个动点（不与B、C重合），连结AD，将线段AD绕点D按顺时针方向旋转90°，使点A旋转到点E，连结EC．
（1）如果点D在线段BC上运动，如图1：求证：
（2）如果点D在线段BC上运动，请写出AC与CE的位置关系．通过观察、交流，小明形成了以下的解题思路：过点E作交直线BC于F，如图2所示，通过证明，可推证等腰直角三角形，从而得出AC与CE的位置关系，请你写出证明过程．
（3）如果点D在线段CB的延长线上运动，利用图3画图分析，（2）中的结论是否仍然成若成立，请证明；若不成立，请说明理由．
【答案】（1）见解析；（2）垂直，理由见解析；（3）成立，证明见解析
【分析】（1）根据直角三角形的性质证明即可；
（2）过点E作交直线BC于F，如图2所示，通过证明，可推证等腰直角三角形，从而得出AC与CE的位置关系；
（3）如图3所示，过点E作于F，证明，进一步可证明
【详解】解：（1）证明：∵
∴
∵
∴
∴
（2）垂直
∵
∴
∵
∴
在和中
∴
∴，
∵
∴，
∴
即．
∴
又∵
∴，且
∴
即．
（3）（2）中的结论仍然成立
如图3所示，过点E作于F
∵
∴
在和中
∴
∴，
∴
即
∴
∴
∴
∴．
【点睛】此题是几何变换综合题，主要考查了旋转的性质，全等三角形的判定和性质，证明是解本题的关键．