初中数学北师大版（2024）七年级上册第一章 丰富的图形世界1.2 展开与折叠课后测评

这是一份初中数学北师大版（2024）七年级上册第一章 丰富的图形世界1.2 展开与折叠课后测评，文件包含北师大版数学七上重难点培优训练专题01立体图形展开与折叠三方向看物体的形状原卷版doc、北师大版数学七上重难点培优训练专题01立体图形展开与折叠三方向看物体的形状解析版doc等2份试卷配套教学资源，其中试卷共31页， 欢迎下载使用。
考点一 立体图形的分类 考点二 几何体中的点、棱、面
考点三 几何体的展开图的认识 考点四 由展开图计算几何体的表面积、体积
考点五 正方体的展开图 考点六 从三个方向看物体的形状
考点一 立体图形的分类
例题：（2022·全国·七年级）将如图几何体分类，并说明理由．
【答案】柱体：①正方体，②长方体，③圆柱体，⑥四棱柱，⑦三棱柱；锥体：④圆锥；球体：⑤球；见解析
【解析】
【分析】
根据立体图形的分类：柱体，锥体，球体，可得答案．
【详解】
解：根据几何体的概念可得，柱体：①正方体，②长方体，③圆柱体，⑥四棱柱，⑦三棱柱；
锥体：④圆锥；
球体：⑤球．
【点睛】
本题考查了认识立体图形，立体图形分为三大类：柱体，锥体，球体．
【变式训练】（2022·全国·七年级专题练习）下列是我们常见的几何体，按要求将其分类（只填写编号）．
(1)如果按“柱”“锥球”来分，柱体有______，椎体有______，球有______；
(2)如果按“有无曲面”来分，有曲面的有______，无曲面的有______．
【答案】(1)①②⑥；③④；⑤
(2)②③⑤；①④⑥
【解析】
【分析】
（1）根据立体图形的特点从柱体的形状特征考虑．
（2）根据面的形状特征考虑．
(1)
解：∵（1）是四棱柱，（2）是圆柱，（3）是圆锥，（4）是棱锥，（5）是球，（6）是三棱柱，
∴柱体有（1），（2），（6），锥体有（3），（4），球有（5），
故答案为：（1），（2），（6）；（3），（4）；（5）；
(2)
∵（2）（3）（5）有曲面，其它几何体无曲面，
∴按“有无曲面”来分，有曲面的有（2），（3），（5），无曲面的有：（1），（4），（6），
故答案为：（2），（3），（5）；（1），（4），（6）．
【点睛】
本题考查了认识立体图形，解决本题的关键是认识柱体的形状特征．
考点二 几何体中的点、棱、面
例题：（2022·全国·七年级专题练习）正方体有________个底面，它们是________边形；它有________个侧面，每一个侧面都是________形；它有________个顶点，________条棱，其中________条侧棱
【答案】 2 正方形 4 正方 8 12 4
【解析】
略
【变式训练】（2022·全国·七年级）如图，图①所示的几何体叫三棱柱，它有6个顶点，9条棱，5个面，图②和图③所示的几何体分别是四棱柱和五棱柱．
(1)四棱柱有 个顶点， 条棱， 个面；
(2)五棱柱有 个顶点， 条棱， 个面；
(3)那么n棱柱有 个顶点， 条棱， 个面．
【答案】(1)8，12，6
(2)10，15，7
(3)2n，3n，（n+2）
【解析】
【分析】
（1）根据棱柱的形体特征进行解答即可；
（2）根据棱柱的形体特征进行解答即可；
（3）根据棱柱的形体特征进行解答即可．
(1)
解：由棱柱的形体特征可知：四棱柱有8个顶点，12条棱，6个面，
故答案是：8，12，6；
(2)
解：由棱柱的形体特征可知：5棱柱有10个顶点，15条棱，7个面，
故答案是：10，15，7；
(3)
解：由棱柱的形体特征可知：n棱柱有2n个顶点，3n条棱，（n+2）个面，
故答案是：2n，3n，（n+2）．
【点睛】
本题主要考查棱柱的特征，掌握棱柱的形体特征是解题的关键．
考点三 几何体的展开图的认识
例题：（2022·广东广州·中考真题）如图是一个几何体的侧面展开图，这个几何体可以是（ ）
A．圆锥B．圆柱C．棱锥D．棱柱
【答案】A
【解析】
【分析】
由图可知展开侧面为扇形，则该几何体为圆锥．
【详解】
该几何体的侧面展开图是扇形，所以这个几何体可能是圆锥,
故选：A．
【点睛】
此题主要考查几何体的展开图，熟记几何体的侧面展开图是解题的关键．
【变式训练】（2022·全国·七年级）如图是几何体的展开图，这个几何体是（ ）
A．圆柱B．三棱锥C．四棱柱D．三棱柱
【答案】D
【解析】
【分析】
由图可知，两个底面是三角形，根据三棱柱的展开图的特征解答即可．
【详解】
解：因为展开图是三个矩形，两个三角形，
所以这个几何体是三棱柱，
故选：D．
【点睛】
本题考查几何体的展开图，三棱柱等知识，解题的关键是掌握三棱柱的展开图的特征．
考点四 由展开图计算几何体的表面积、体积
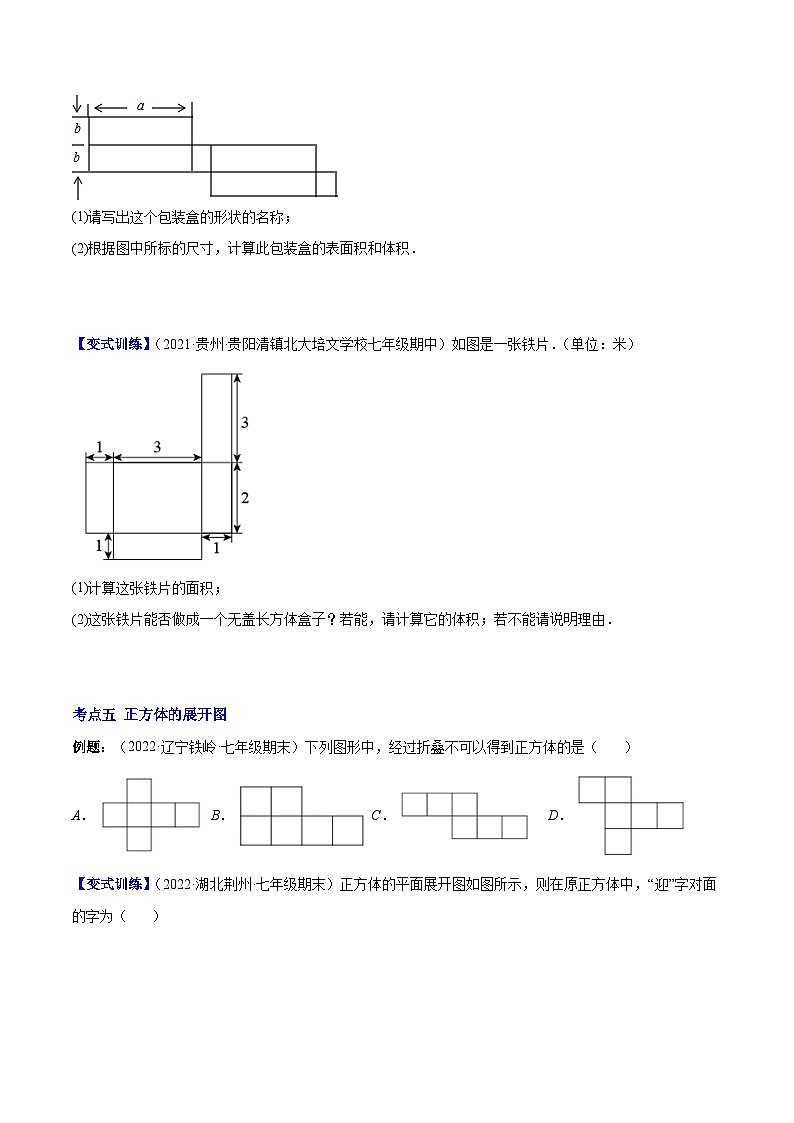
例题：（2021·全国·七年级单元测试）如图是一个食品包装盒的表面展开图．

(1)请写出这个包装盒的形状的名称；
(2)根据图中所标的尺寸，计算此包装盒的表面积和体积．
【答案】(1)此包装盒是一个长方体
(2)此包装盒的表面积为： SKIPIF 1 < 0 ，体积为： SKIPIF 1 < 0 ．
【解析】
【分析】
（1）根据图示可知有四个长方形和2个正方形组成，故可知是长方体；
（2）根据长方体的表面积公式和体积公式分别进行计算即可．
(1)
由展开图可以得出：此包装盒是一个长方体．
(2)
此包装盒的表面积为：2×b2+4×ab=2b2+4ab；
体积为b2×a=ab2．
【点睛】
此题考查了几何体的展开图，用到的知识点是长方体的表面积公式和体积公式，解题的关键是找出长方体的长、宽和高．
【变式训练】（2021·贵州·贵阳清镇北大培文学校七年级期中）如图是一张铁片．（单位：米）
(1)计算这张铁片的面积；
(2)这张铁片能否做成一个无盖长方体盒子？若能，请计算它的体积；若不能请说明理由．
【答案】(1)16m2；
(2)能，6m3．
【解析】
【分析】
（1）把图形分为两个长方形，一个正方形求解即可；
（2）折叠图形，利用体积公式求解即可．
(1)
解：由题意可得
S＝1×2+3×3+1×5＝16（m2）；
答：这张铁片的面积是16 m2．
(2)
解：能，如图：
盒子的体积V＝3×2×1＝6（m3）．
答：这张铁片能做成一个无盖长方体盒子，体积是6m3．
【点睛】
本题主要考查了整式的混合运算及展开图折叠成几何体，解题的关键是正确的列出算式求解．
考点五 正方体的展开图
例题：（2022·辽宁铁岭·七年级期末）下列图形中，经过折叠不可以得到正方体的是（ ）
A．B．C．D．
【答案】B
【解析】
【分析】
由平面图形的折叠及正方体的展开图的常见形式作答即可．
【详解】
解：选项A为1-4-1型、C为3-3型、D为1-3-2型经过折叠均能围成正方体；
B、有“田”字格，不能折成正方体．
故选：B．
【点睛】
本题主要考查展开图折叠成几何体的知识点，注意只要有“凹”“田”字格的展开图都不是正方体的表面展开图．
【变式训练】（2022·湖北荆州·七年级期末）正方体的平面展开图如图所示，则在原正方体中，“迎”字对面的字为（ ）
A．北B．京C．冬D．奥
【答案】D
【解析】
【分析】
根据正方体的平面展开图找相对面的方法，“Z”字两端是对面，判断即可．
【详解】
在原正方体中，“迎”字的对面的字为“奥”．
故选：D．
【点睛】
此题考查正方形的平面展开图相对面上的字，熟记正方体的平面展开图的特点及几种形式是解题的关键．
考点六 从三个方向看物体的形状
例题：（2022·黑龙江哈尔滨·七年级期末）下列各选项中水平放置的几何体，从左面看不是长方形的是( )
A．B．C．D．
【答案】B
【解析】
【分析】
根据左视图是从左面看到的视图，从而结合选项逐项判定左视图即可得到结论．
【详解】
解：A、圆柱的左视图是长方形，故本选项不符合题意
B、圆锥的左视图是等腰三角形，故本选项符合题意；
C、三棱柱的左视图是长方形，故本选项不符合题意；
D、长方体的左视图是长方形，故本选项不符合题意；
故选：B．
【点睛】
本题考查了简单几何体的三视图-左视图，熟练掌握常见几何体的三视图是解题的关键．
【变式训练】（2022·山东临沂·七年级期末）如图所示的几何体是由5个大小相同的小正方体搭成的．从左面看到的平面图形是（ ）
A．B．C．D．
【答案】A
【解析】
【分析】
根据从左面看得到的图形是左视图，可得答案．
【详解】
从左面看第一层有三个小正方形，第二层有一个小正方形；第一列有一个小正方形，第二列有两个小正方形，第三列有一个小正方形．
故选A．
【点睛】
本题考查了简单组合体的三视图，从左面看得到的图形是左视图．
一、选择题
1．（2021·陕西·西安市曲江第一中学七年级期中）图中的图形是由某立方体图形展开得到的，则该立方体图形是（ ）
A．长方体B．圆锥C．圆柱D．球体
【答案】C
【解析】
【分析】
根据圆柱表面展开图的特点解题即可．
【详解】
解：观察图形，由立体图形及其表面展开图的特点可知相应的立体图形是圆柱．
故选：C．
【点睛】
本题考查圆柱表面展开图，记住圆柱的表面展开图是解题的关键．
2．（2022·贵州毕节·七年级期末）2021年，毕节市顺利获评为全国文明城市，为此小颖特别制作了一个正方体玩具，其展开图如图所示，则原正方体中与“文”字相对的字是（ ）
A．全B．城C．市D．明
【答案】B
【解析】
【分析】
正方体的表面展开图，相对的面之间一定相隔一个正方形，根据这一特点作答．
【详解】
解：正方体的表面展开图，相对的面之间一定相隔一个正方形，
∴“全”与“市”相对，“文”与“城”相对，“明”与“国”相对，
故选：B．
【点睛】
本题主要考查了正方体相对两个面上的文字，注意正方体的空间图形，从相对面入手，分析及解答问题．
3．（2022·山东·烟台市福山区教学研究中心期末）如图，这是一个机械零部件，箭头指的方向是正面，该零部件的从左面看到的形状图是（ ）
A．B．C．D．
【答案】C
【解析】
【分析】
根据圆柱平放从左面看的形状图是圆，圆柱正立从正面看的形状图是长方形，结合放置位置判断即可．
【详解】
解：因为圆柱平放从左面看的形状图是圆，圆柱正立从正面看的形状图是长方形，
所以从左面看到的形状图是．
故选：C．
【点睛】
此题考查了三视图，解题的关键是掌握从左面看的含义，注意能看到的立体图形中的线条都要画成实线，看不到的画成虚线．
4．（2022·浙江台州·七年级期末）如图所示，该正方体的展开图为（ ）
A．B．
C．D．
【答案】D
【解析】
【分析】
根据正方体的展开与折叠，正方体展开图的形状进行判断即可．
【详解】
解：根据正方体表面展开图的“相对的面”的判断方法可知，
选项B中面“v”与“＝”是对面，因此选项B不符合题意；
再根据上面“v”符号开口，可以判断选项D符合题意；选项A、C不符合题意；
故选：D．
【点睛】
本题考查几何体的展开图，掌握正方体展开图的特征是正确判断的前提．
二、填空题
5．（2022·江苏淮安·七年级期末）如图，要使图中平面展开图按虚线折叠成正方体后，相对面上两个数之积为8，则x+y＝_____．
【答案】6
【解析】
【分析】
根据正方体的表面展开图找相对面的方法，“Z”字两端是对面求出x，y的值，然后代入式子进行计算即可．
【详解】
解：由图可知：
2与x相对，4与y相对，
∵相对面上两个数之积为8，
∴2x＝8，4y＝8，
∴x＝4，y＝2，
∴x+y＝6，
故答案为：6．
【点睛】
本题考查了正方体相对两个面上的文字，有理数的乘法，熟练掌握根据正方体的表面展开图找相对面的方法是解题的关键．
6．（2022·湖北孝感·七年级期末）如图是一个长方体的表面展开图，其中四边形ABCD是正方形，根据图中标注的数据可求得原长方体的积是_______．
【答案】 SKIPIF 1 < 0 ##16立方厘米
【解析】
【分析】
根据题意可得原长方体的宽的4倍等于8cm，原长方体的高与长的和为6cm，再由四边形ABCD是正方形，可求出原长方体的长，从而得到原长方体的高，即可求解．
【详解】
解：根据题意得：原长方体的宽的4倍等于8cm，原长方体的高与长的和为6cm，
∴原长方体的宽为 SKIPIF 1 < 0 ，
∵四边形ABCD是正方形，
∴原长方体的长等于2×2=4cm，
∴原长方体的高等于6-4=2cm，
∴原长方体的积是 SKIPIF 1 < 0 ．
故答案为： SKIPIF 1 < 0
【点睛】
此题主要考查了几何体的展开图，利用已知图形得出各边长是解题关键，用到的知识点是几何体的展开图和长方体的体积公式．
7．（2021·四川成都·七年级期中）有一块积木，每一块的各面都涂上红绿黑白蓝黄六种不同的颜色，下面是它摆放的三种不同方向的图像，请根据图像判断绿色面的对面是_____色
【答案】黄
【解析】
【分析】
根据图形可得涂有绿色一面的邻边是白，黑，红，蓝，即可得到结论．
【详解】
解：∵涂有绿色一面的邻边是白，黑，红，蓝，
∴涂成绿色一面的对面的颜色是黄色，
故答案为：黄．
【点睛】
本题考查了正方体相对两个面上的文字问题，此类问题可以制作一个正方体，根据题意在各个面上标上图案，再确定对面上的图案，可以培养动手操作能力和空间想象能力．
8．（2022·全国·七年级课时练习）一个几何体由若干个大小相同的小立方块搭成，从左面和上面看到的平面图形如图所示，则搭成这个几何体的小立方块的个数为_____．
【答案】4
【解析】
【分析】
根据左面看与上面看的图形，得到俯视图解答即可．
【详解】
解：根据左视图和俯视图，这个几何体的底层有3个小正方体，
第二层有1个小正方体，
所以有 SKIPIF 1 < 0 个小正方体，
故答案为：4．
【点睛】
本题主要考查从不同方向看几何体，熟练掌握几何体的特征是解题的关键．
三、解答题
9．（2021·全国·七年级专题练习）将图中的几何体进行分类，并说明理由．
【答案】见解析．
【解析】
【分析】
首先要确定分类标准，可以按组成几何体的面的平或曲来划分，也可以按柱、锥、球来划分．
【详解】
解：若按形状划分：（1）（2）（6）（7）是一类，组成它的各面全是平面；（3）（4）（5）是一类，组成它的面至少有一个是曲面．
若按构成划分：（1）（2）（4）（7）是一类，是柱体；（5）（6）是一类，即锥体；（3）是球体．
【点睛】
本题主要考查了几何体的分类，解题的关键在于先根据立体图形的底面的个数，确定它是柱体、锥体还是球体，再根据其侧面是否为多边形来判断它是圆柱(锥)还是棱柱(锥)．
10．（2020·辽宁沈阳·七年级期中）如图是某几何体从不同方向看到的图形．
（1）写出这个几何体的名称；
（2）若从正面看得到的长方形的长为 SKIPIF 1 < 0 ，从上面看得到的圆的直径为 SKIPIF 1 < 0 ，求这个几何体的侧面积（结果保留 SKIPIF 1 < 0 ）．
【答案】（1）圆柱；（2） SKIPIF 1 < 0
【解析】
【分析】
（1）根据该几何体的主视图与左视图是矩形，俯视图是圆可以确定该几何体是圆柱；
（2）根据告诉的几何体的尺寸确定该几何体的侧面积即可．
【详解】
解：（1）这个几何体是圆柱
（2）∵从上面看得到的圆的直径为 SKIPIF 1 < 0 ，
从正面看得到的长方形的长为 SKIPIF 1 < 0 ．
∴该圆柱的底面直径为 SKIPIF 1 < 0 ，高为 SKIPIF 1 < 0 ．
∴该几何体的侧面积为 SKIPIF 1 < 0 ．
【点睛】
本题考查了由三视图判断几何体及几何体的表面积问题，解题的关键是了解圆柱的侧面积的计算方法．
11．（2022·全国·七年级课时练习）如图所示的是一个长方体的表面展开图，每个面上都标注了字母（字母朝外），回答下列问题：
(1)如果面 SKIPIF 1 < 0 在长方体的底部放置，那么哪一个面会在它的上面？
(2)如果面 SKIPIF 1 < 0 在前面，从左面看是面 SKIPIF 1 < 0 ，那么哪一个面会在上面？
(3)从右面看是面 SKIPIF 1 < 0 ，面 SKIPIF 1 < 0 在左面，那么哪一个面会在上面？
【答案】(1)F面
(2)“C”面或“E面
(3)“B面或“D面
【解析】
【分析】
根据长方体表面展开图的特征进行判断即可．
（1） SKIPIF 1 < 0 根据“相间、 SKIPIF 1 < 0 端是对面”可知，“ SKIPIF 1 < 0 ”与“ SKIPIF 1 < 0 ”相对，“ SKIPIF 1 < 0 ”与“ SKIPIF 1 < 0 ”相对，“ SKIPIF 1 < 0 ”与“ SKIPIF 1 < 0 “相对，所以面A在长方体的底部，那么 SKIPIF 1 < 0 面会在它的上面；
（2）若面 SKIPIF 1 < 0 在前面，左面是面 SKIPIF 1 < 0 ，则“ SKIPIF 1 < 0 ”在后面，“ SKIPIF 1 < 0 ”在右面，此时“ SKIPIF 1 < 0 ”在上面，“ SKIPIF 1 < 0 ”在下面，或“ SKIPIF 1 < 0 ”在上面，“ SKIPIF 1 < 0 ”在下面；答：如果面 SKIPIF 1 < 0 在前面，从左面看是面 SKIPIF 1 < 0 ，那么“ SKIPIF 1 < 0 ”面或“ SKIPIF 1 < 0 ”面会在上面；
（3）从右面看是面 SKIPIF 1 < 0 ，面 SKIPIF 1 < 0 在左面，则“ SKIPIF 1 < 0 ”面或“ SKIPIF 1 < 0 ”面在上面．
【点睛】
本题考查长方体的展开与折叠，掌握长方体表面展开图的特征是解决问题的关键．
12．（2021·辽宁·阜新市第一中学七年级期中）图1是正方体的平面展开图，六个面的点数分别为1点、2点、3点、4点、5点、6点，将点数朝外折叠成一枚正方体骰子，并放置于水平桌面上，如图2所示．
（1）在图2所示的正方体骰子中，1点对面是 点；2点的对面是 点（直接填空）；
（2）若骰子初始位置为图2所示的状态，将骰子向右翻滚90°，则完成1次翻转，此时骰子朝下一面的点数是2，那么按上述规则连续完成2次翻转后，骰子朝下一面的点数是 点；连续完成2021次翻转后，骰子朝下一面的点数是 点（直接填空）．
【答案】（1）6；5；（2）3；2
【解析】
【详解】
（1）正方体的表面展开图，相对面之间一定相隔一个正方形，
“2点”与“5点”是相对面，“3点”与“4点”是相对面，“1点”与“6点”是相对面，
故答案为：6,5
（2）观察图2即可知，上述规则连续完成2次翻转后，骰子朝下一面的点数是3
根据题意，每四次一循环，
∵ SKIPIF 1 < 0 ，
∴完成2021次翻转为第506组的第一次翻转，
∴骰子朝下一面的点数是2．
故答案为：3,2
【点睛】
本题主要考查正方体的表面展开图各个面上的数字规律，掌握相对面上的数字规律，是解题的关键．
13．（2021·全国·七年级专题练习）如图是从三个方向看几何体得到的形状图．
（1）说出这个几何体的名称；
（2）画出它的一种表面展开图；
（3）若从正面看到的形状图的宽为4 cm，长为7 cm，从左面看到的形状图的宽为3 cm，从上面看到的形状图中斜边长为5 cm，求这个几何体所有棱长的和，以及它的表面积和体积．
【答案】（1）三棱柱；（2）见解析；（3）这个几何体所有棱长的和为45cm，它的表面积为96cm2，体积为42cm3
【解析】
【分析】
（1）根据三棱柱的三视图特征即可解答；
（2）根据三棱柱的三视图特征，画出其表面展开图即可，答案不唯一；
（3）根据题意可知，侧棱为7，共3条，两个底面三角形的三边长为3、4、5，继而相加即可求得棱长的和，结合表面积等于三个侧面与两个底面的面积和求得表面积，根据体积＝底面积×侧棱即可求解．
【详解】
解：（1）这个几何体是三棱柱，
（2）表面展开图如图所示（答案不唯一）：
（3）棱长和为：7×3+（3+4+5）×2=45cm
表面积为：S=S（底）+S（侧）= SKIPIF 1 < 0 ×3×4×2+（3+4+5）×7=96cm SKIPIF 1 < 0
体积为：V=S（底）×h= SKIPIF 1 < 0 ×3×4×7=42cm3
故：这个几何体所有棱长的和为45cm，它的表面积为96cm SKIPIF 1 < 0 ，体积为42cm SKIPIF 1 < 0 ．
【点睛】
本题主要考查三棱柱有关知识，解题的关键是熟练掌握三棱柱的特征，三视图，表面积及体积计算公式．
14．（2022·全国·七年级专题练习）观察表中的几何体，解答下列问题：
(1)补全表中数据；
(2)观察表中的数据，推测n棱柱的顶点数为 ，棱数为 ，面数为 ．（用含n的式子表示）
【答案】(1)8，15，8，见解析
(2)2n，3n，n+2
【解析】
【分析】
（1）根据四棱柱上面4个顶点，下面四个顶点可以知道四棱柱的顶点数；五棱柱上底面5条棱，下底面5条棱，侧棱5条可以知道五棱柱的棱数；根据六棱柱有6个侧面和2个底面知道六棱柱的面数；
（2）根据表格推测即可．
(1)
解：∵四棱柱上面4个顶点，下面四个顶点，
∴四棱柱的顶点数是8；
∵五棱柱上底面5条棱，下底面5条棱，侧棱5条，
∴五棱柱的棱数是15；
∵六棱柱有6个侧面和2个底面，
∴六棱柱的面数是8；
故答案为：8；15；8；
(2)
解：n棱柱的顶点数为2n，
棱数为3n，
面数为n+2，
故答案为：2n；3n；n+2．
【点睛】
本题主要考查几何体的初步认识，熟练掌握棱柱的概念是解题的关键．
全
国
文
明
城
市
名称
三棱柱
四棱柱
五棱柱
六棱柱
图形
顶点数a
6

10
12
棱数b
9
12

18
面数c
5
6
7

名称
三棱柱
四棱柱
五棱柱
六棱柱
图形
顶点数a
6
8
10
12
棱数b
9
12
15
18
面数c
5
6
7
8