2023~2024学年山东省青岛市城阳区九年级(上)期中数学试卷(解析版)

这是一份2023~2024学年山东省青岛市城阳区九年级(上)期中数学试卷(解析版)，共17页。试卷主要包含了作图题请用直尺，解答题等内容，欢迎下载使用。
第Ⅰ卷（共30分）
一、选择题（ 本大题共10小题，每小题3分，共30分）在每小题给出的四个选项中，只有一项是符合题目要求的．
1. 方程的根是（ ）
A. B.
C. ，D. ，
【答案】D
【解析】，
移项得：，
∴，
解得：，，
故选D．
2. 若四条线段a，b，c，d成比例，其中2cm，4cm，6cm，则线段c的长为（ ）
A. 1cmB. 3cmC. 9cmD. 12cm
【答案】B
【解析】是成比例线段，
，
2cm，4cm，6cm，
．
故选：B．
3. 菱形具有而矩形不一定具有的性质是 ( )
A. 对角线互相垂直B. 对角线相等
C. 对角线互相平分D. 对角互补
【答案】A
【解析】菱形的对角线互相垂直平分，矩形的对角线相等互相平分，
则菱形具有而矩形不一定具有的性质是：对角线互相垂直，
故选A．
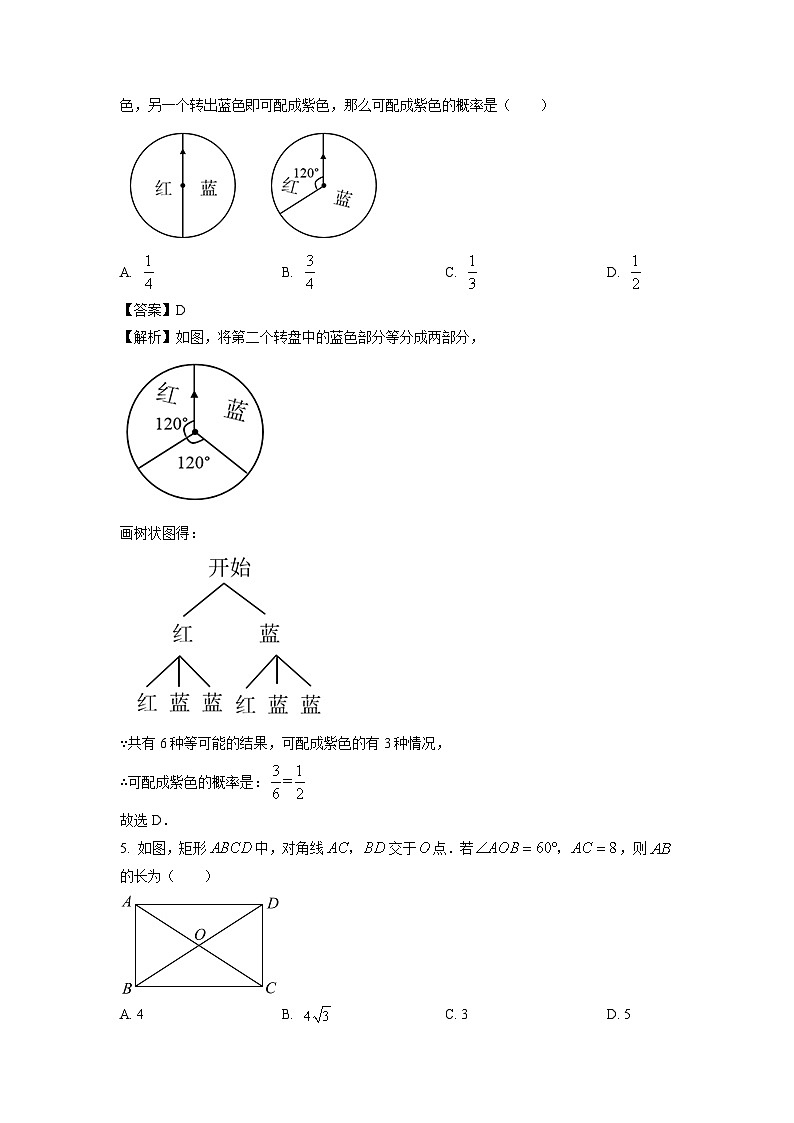
4. 用图中两个可自由转动的转盘做“配紫色”游戏：分别旋转两个转盘，若其中一个转出红色，另一个转出蓝色即可配成紫色，那么可配成紫色的概率是（ ）
A. B. C. D.
【答案】D
【解析】如图，将第二个转盘中的蓝色部分等分成两部分，
画树状图得：
∵共有6种等可能的结果，可配成紫色的有3种情况，
∴可配成紫色的概率是：
故选D．
5. 如图，矩形中，对角线交于点．若，则的长为（ ）

A. 4B. C. 3D. 5
【答案】A
【解析】∵四边形是矩形，
∴，，，
∴，
∵，
∴是等边三角形，
∴，
故选：．
6. 某商场品牌手机经过5，6月份连续两次降价每部售价由5000元降到3600元．且第一次降价的百分率是第二次的2倍，设第二次降价的百分率为，根据题意可列方程（ ）
A. B.
C. D.
【答案】A
【解析】设第二次降价的百分率为x，则第一次降价的百分率为2x，
根据题意，得：，
故选：A．
7. 如图，“笔尖”图案五边形由正方形和等边组成，连接，，则的度数为（ ）

A. B. C. D.
【答案】D
【解析】四边形是正方形，
，，
是等边三角形，
，，
，
，，
，
，
，
同理可得：，
，
故选：D．
8. 输入一组数据，按下列程序进行计算，输出结果如表：
分析表格中的数据，估计方程(x＋8)2－826＝0的一个正数解x的大致范围为（ ）
A. 20.5＜x＜20.6B. 20.6＜x＜20.7
C. 20.7＜x＜20.8D. 20.8＜x＜20.9
【答案】C
【解析】由表格可知，当x=20.7时，（x+8）2-826=-2.31，当x=20.8时，（x+8）2-826=3.44，
故（x+8）2-826=0时，20.7＜x＜20.8，故选C．
9. “黄金分割”给人以美感，它不仅在建筑、艺术等领域有着广泛应用，而且在大自然中处处有美的痕迹，一片小小的树叶也蕴含着“黄金分割”．如图，P为的黄金分割点，如果的长度为，那么的长度是（ ）

A. B.
C. D.
【答案】D
【解析】∵P为的黄金分割点，的长度为，
∴，
故选：D．
10. 如图，在边长为 1的正方形中，分别是边上的动点，分别是的中点，则的最大值为（ ）
A. B. 0.5C. 1D. 2
【答案】A
【解析】连接，
分别是的中点，
是的中位线，，
四边形是正方形，且边长为1，
，，
，
当最大时，最大，此时最大，
点是上动点，
当点和点重合时，最大，即的长度，
此时，
，
的最大值为，
故选：A．
第Ⅱ卷（共90分）
二、填空题（ 本大题共6小题，每小题3分，共18分）请将 11—16各小题的答案填写在答题纸规定的位置．
11. 若，则=______.
【答案】
【解析】∵=，b+d≠0，∴=．
故答案为．
12. 现有大小相同的正方形纸片若干张，小明想用其中的3张拼成一个如图所示的长方形，小芳也想拼一个与它形状相同但比它大的长方形，则她最少要用_____张正方形纸片（每个正方形纸片不得剪开）．

【答案】12
【解析】∵正方形纸片大小相同，
∴拼一个与它形状相同但比它大的长方形，至少长和宽各是原来的2倍，
∴需要正方形的纸片是张，
故答案为：12．
13. 一个口袋中装有10个红球和若干个黄球．在不允许将球倒出来数的前提下，为估计口袋中黄球的个数，小明采用了如下的方法：每次先从口袋中摸出10个球，求出其中红球数与10的比值，再把球放回口袋中摇匀．不断重复上述过程20次，得到红球数与10的比值的平均数为0.4．根据上述数据，估计口袋中大约有_______个黄球
【答案】15
【解析】∵小明通过多次摸球实验后发现其中摸到红色球的频率稳定在0.4，
设黄球有x个，
∴0.4（x+10）=10，
解得x=15．
故答案为：15
14. 如图,两张等宽的纸条交叉叠放在一起,重合部分构成一个四边形， ，，则纸条的宽度为_________．
【答案】
【解析】如图，作交于，作交于，连接交于，
，
两条纸条宽度相同，
，
，，
四边形是平行四边形，
，
，
四边形是菱形，
，，，，
，
，
，
，
，
纸条的宽度为，
故答案为：．
15. 某种服装，平均每天可销售30件，每件赢利40元，网查发现，若每件降价1元，则每天可多售6件，如果每天要赢利2100元，每件应降价多少元？设该服装每件降价x元，根据题意可列方程____．
【答案】
【解析】设每件应降价x元，
依题意得：，
故答案为：．
16. 如图，已知四边形,,,,，，分别取的中点,连接，过点作于点，下列结论：①；②；③；④．其中正确的是 ________．（只填写序号）

【答案】①②④
【解析】在中，，，，
，
、分别是的中点，
是的中位线，
，故①正确，符合题意；
，
，
，
，
，
，
，
，故②正确，符合题意；
，，，
，故③错误，不符合题意；
如图，连接，

，为的中点，
，
，，
，
四边形是矩形，
，
，
为的中点，
，
，
，即，
解得，
，故④正确，符合题意；
综上所述，正确的有①②④，
故答案为：①②④．
三、作图题（本大题满分4分）请用直尺、圆规作图，不写作法，但要保留作图痕迹．
17. 已知：．

求作：菱形，使点为的中点，点在边上，点在的内部．
解：菱形如图所示，

由作图可得，
四边形是菱形．
四、解答题 （本大题共8小题，满分68分）
18. 解方程：
（1）（配方法）；
（2）．
解：（1），
，
，即，
，
，，
原一元二次方程的解为：，；
（2），
，
，
或，
解得：，，
原一元二次方程的解为：，．
19. 已知关于x的一元二次方程 ．
（1）若方程有实数根，求实数m 的取值范围；
（2）若方程的一个根为 1，求方程的另一个根．
解：（1）∵关于x的一元二次方程 有实数根，
∴，
∴，
解得．
（2）设方程的另一个根为，
∵方程的一个根为 1，
∴，
解得，
故方程的另一个根为1．
20. 2023年10月 15 日，由青岛市城阳区人民政府与市体育局、高新区管委、青岛市广播电视台等主办的青岛海上马拉松顺利开展．本次活动突出青岛特色，体现城阳元素，展示城市形象，是国内唯一的跨海大桥马拉松．大学生小亮和小明报名参加赛会志愿者活动，两人分别从以下三项活动中随机选择一项，：赛事记录，：现场引导，：散场清理．请用列表或画树状图的方法求两人恰好选择同一项服务内容的概率．
解：画树状图如图所示：
，
共有9个等可能的结果，小亮和小明两人恰好选中同一项服务内容的结果有3种，
小亮和小明两人恰好选中同一项服务内容的概率为．
21. 如图① ，在中， ，．点D，E分别在边上，且．

（1）在图①中，则 的值为 ；
（2）图①中． 保持不动，将 绕点A 按顺时针方向旋转到图②的位置，其它条件不变，连接，则（1）中的结论是否仍然成立? 请说明理由．
解：（1），
，
，
，
，，
；
（2）由题可知，
由（1）知，，
，
，
，，
．
22. “关爱儿童健康，创建育人环境”，某幼儿园教室矩形地面的长为，宽为，现准备在地面铺设一块面积为 的地毯，如图所示，一边靠墙，另三周未铺地毯的条形区域的宽度都相同，求未铺地毯的条形区域的宽度．
解：设未铺地毯的条形区域的宽度为，
由题意得：，
整理，得：，
解得：，，
，解得：，
，
答：未铺地毯的条形区域的宽度为．
23. 已知：如图中，在上截取，连接，取的中点，过点作，交线段的延长线于点，连接．

（1）求证：；
（2）请你给添加一个条件，使四边形成为正方形，并说明理由．
解：（1）点为的中点，
，
，
，
在和中，
，
，
；
（2），
理由如下：由（1）得：，
，
四边形是平行四边形，
，
四边形是菱形，
，
四边形正方形．
24. 某市政府大力扶持大学生创业．小华在政府的扶持下投资销售一种进价为每件20元的护眼台灯．销售过程中发现，当售价为25元时，每月销售250件；当售价为30元时，每月销售 200件，销售量与销售单价成一次函数关系．如果小华想要每月获得2000元的利润，为了让顾客得到实惠，应将销售单价应定为多少元?
解：设销售量为元，销售单价为件，，
将，与，代入函数解析式中，，
解得，
，
，
即，
解得或（舍去），
答：小华想要每月获得2000元的利润，销售单价应定为30元．
25. 【问题提出】
有编号分别为1，2，3，…， n （n为正整数，且）的n个球, 甲、 乙轮流抓，每次可以抓1个球或相连编号的 2个球．甲先抓，规定谁抓到最后一次谁获胜．甲第1次应该怎样抓才能获胜?
【问题探究】
我们采取一般问题特殊化的策略，先从最简单的情形入手，再逐次递进，从中找规律．
（1）如图①，当n=1时，甲一次抓一个球就可以抓完，显然甲获胜，
（2）如图②，当 n=2时，甲一次抓编号相连的1号和2号2个球就可以抓完，所以甲获胜．
（3）如图③，当n=3时，甲第1次先抓2号球，乙第1次无论抓1号球还是3号球，最后还剩1个球，甲第2次抓就可以抓完，所以甲获胜．
（4）如图④，当n=4时，甲第1次先抓编号相连的2号和3号球，乙第1次无论抓1号球还是4号球，最后还剩1个球，甲第2次抓就可以抓完，所以甲获胜．

（5）如图⑤，当n=5时，甲第1次先抓3号球，乙第1次抓有两类抓法：
一类：一次抓1个球. 若乙第1次从1号和2号中任抓1个球，则甲第2次从4号和5号中任抓1个球，乙第2次无论抓那个球，最后还剩1个球，甲第3次抓就可以抓完，甲获胜．同理，若乙第1次从4号和5号中任抓1个球， 甲也会获胜．
二类：一次抓相连编号的2个球，若乙第1次抓编号相连的1号和2号球，则甲第2次抓编号相连的4号和5号球就可以抓完，甲获胜．同理，若乙第1次抓编号相连的4号和5号球，甲也会获胜．
（6）如图⑥，当n=6时， 甲第1次应该怎样抓第1次应该抓 号球．

（7）如图⑦， 当n=7时， 甲要获胜， 第1次应该抓 号球．

【问题解决】
有编号分别为 1，2，3， ...，n （n为正整数，且n>1）的n个球，甲、 乙轮流抓，每次可以抓1个球或相连编号的2个球．甲先抓，规定谁抓到最后一次谁获胜．甲第1次应该怎样抓才能获胜? （ 只写出结论）．
【拓展应用】
有编号分别为1，2， 3，…，（ n为正整数，且n≥1）的n个球，甲、乙轮流抓，每次可以抓 1个球或相连编号的2个球．甲先抓，规定谁抓到最后一次谁获胜．若甲第1次抓2023号球，最后甲获胜，则n= ．
解：【问题探究】
（6）仿照（1）-（5）可知：甲第1次先抓3号球和4号球，则乙第1次抓有两类抓法：
一类：一次抓1个球. 若乙第1次从1号和2号中任抓1个球，则甲第2次从4号和5号中任抓1个球，乙第2次无论抓那个球，最后还剩1个球，甲第3次抓就可以抓完，甲获胜．同理，若乙第1次从5号和6号中任抓1个球， 甲也会获胜．
二类：一次抓相连编号的2个球，若乙第1次抓编号相连的1号和2号球，则甲第2次抓编号相连的5号和6号球就可以抓完，甲获胜．同理，若乙第1次抓编号相连的4号和5号球，甲也会获胜．
故答案为3号球和4号球；
（7）同理：甲第1次先抓4号球可以获胜．
故答案为4．
【问题解决】当，直接可以获胜；当时，
①n为奇数时，第一次甲第1次应该抓这个球可获胜；
②n为偶数时，第一次甲第1次应该抓和两个球，才能获胜．
【拓展应用】若甲第1次抓2023号球，最后甲获胜，
则有，
即．
故答案为4045．
26. 已知： 如图，在中，，．点P从点A出发，沿方向匀速运动，速度为；同时，点Q从点C出发， 沿方向匀速运动，速度为．过点Q作，与相交于点 D，连接．
设运动时间为，解答下列问题：
（1）当t为何值时，点A在线段的垂直平分线上?
（2）在运动过程中，是否存在某一时刻t，使 ？若存在，求出t的值；若不存在，请说明理由．
（3）当t为何值时，?
解：（1）∵在中，，，
∴，
由题意得，，则，
∵点A在线段的垂直平分线上，
∴，
∴，
解得；
答：当时，点A在线段的垂直平分线上；
（2）作于点E，如图，
∵，，
∴，
∴，即，
∴，，
∵，
∴，
∵，
∴，即，
∴，
整理得，
解得，，
∴存在，当或时，使；
（3）同（2）得，，
∴，
∵，
∴是等腰直角三角形，
∴，即，
解得，
答：当时，．
x
20.5
20.6
20.7
20.8
20.9
输出
－13.75
－8.04
－2.31
3.44
9.21