河北省沧州市南皮县桂和中学2024-2025学年九年级上学期第一次月考数学试题（解析版）-A4

这是一份河北省沧州市南皮县桂和中学2024-2025学年九年级上学期第一次月考数学试题（解析版）-A4，共18页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共12个小题，每小题3分，共36分．在每小题给出的四个选项中，只有一项是符合题目要求的）
1. 一组数据：，则这组数据的众数是（ ）
A. B. C. 1D. 2
【答案】C
【解析】
【分析】本题主要考查了求一组数据的众数，一组数据中出现次数最多的数据叫做这组数据的众数，据此求解即可．
【详解】解：∵数据中，1出现了2次，出现的次数最多，
∴这组数据的众数为1，
故选：C．
2. 下列方程中是一元二次方程是（ ）
A. B. C. D.
【答案】C
【解析】
【分析】本题考查了一元二次方程的定义，方程的两边都是整式，只含有一个未知数，并且整理后未知数的最高次数都是2，像这样的方程叫做一元二次方程．根据一元二次方程的定义逐项分析即可．
【详解】解：A．含有2个未知数，故不是一元二次方程；
B．的分母含未知数，故不是一元二次方程；
C．是一元二次方程；
D．当时，不是一元二次方程；
故选C．
3. 学校举办了以“不负青春，强国有我”为主题的演讲比赛．已知某位选手的礼仪服装、语言表达、举止形态这三项的得分分别为90分，85分，82分，若依次按照的比例确定成绩，则该选手的成绩是（ ）
A. 86分B. 85分C. 84分D. 83分
【答案】A
【解析】
【分析】本题考查了加权平均数的运用，根据加权平均数的计算方法计算即可．
详解】解：（分），
故选：A ．
4. 已知关于的方程的一个根为-2，则实数的值为（ ）
A. B. C. D. -2
【答案】A
【解析】
【分析】根据一元二次方程的根的定义,将根代入进行求解．
【详解】∵x=−2是方程的根,由一元二次方程的根的定义,可得(−2)2+2k−6=0，
解此方程得到k=1.
故选A.
【点睛】考查一元二次方程根的定义，使方程左右两边相等的未知数的值就是方程的解，又叫做方程的根.
5. 统计中能用来比较两人成绩稳定程度的统计量是（ ）
A. 平均数B. 中位数C. 众数D. 方差
【答案】D
【解析】
【分析】根据方差的意义：体现数据的稳定性，集中程度，波动性大小；方差越小，数据越稳定．要比较两位同学在五次数学测验中谁的成绩比较稳定，应选用的统计量是方差．
【详解】解：由于方差反映数据的波动情况，
所以统计中能用来比较两人成绩稳定程度的统计量是方差．
故选：D．
【点睛】此题主要考查统计的有关知识，主要包括平均数、中位数、众数、方差的意义．反映数据集中程度的统计量有平均数、中位数、众数、方差等，各有局限性，因此要对统计量进行合理的选择和恰当的运用．
6. 一元二次方程的二次项系数、一次项系数、常数项分别是（ ）
A. B. C. D.
【答案】C
【解析】
【分析】本题考查了一元二次方程的一般形式，将方程整理成一般形式，注意各系数需要带上前面的正负号即可.
【详解】解：该一元二次方程的一般形式为：，
∴二次项系数、一次项系数、常数项分别是,
故选：C ．
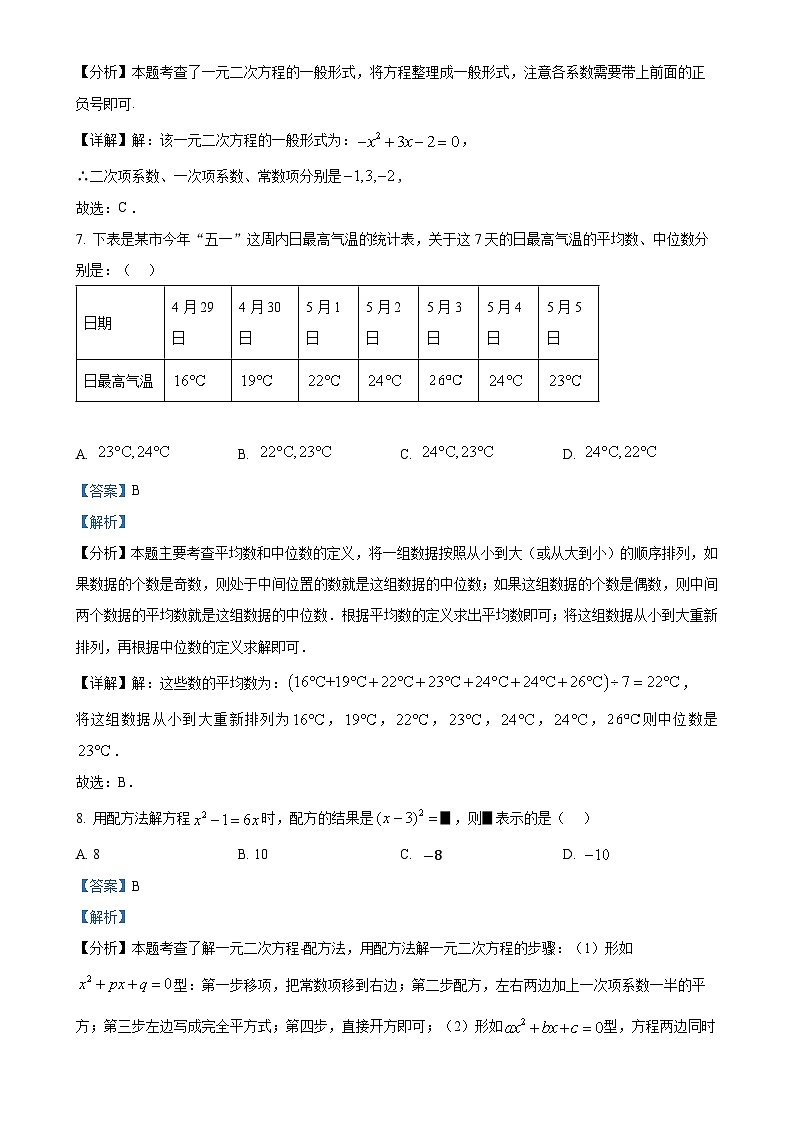
7. 下表是某市今年“五一”这周内日最高气温的统计表，关于这7天的日最高气温的平均数、中位数分别是：（ ）
A. B. C. D.
【答案】B
【解析】
【分析】本题主要考查平均数和中位数的定义，将一组数据按照从小到大（或从大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数；如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数．根据平均数的定义求出平均数即可；将这组数据从小到大重新排列，再根据中位数的定义求解即可．
【详解】解：这些数的平均数为：，
将这组数据从小到大重新排列为，，，，，，则中位数是．
故选：B．
8. 用配方法解方程时，配方的结果是▊，则▊表示的是（ ）
A. 8B. 10C. -8D.
【答案】B
【解析】
【分析】本题考查了解一元二次方程-配方法，用配方法解一元二次方程的步骤：（1）形如型：第一步移项，把常数项移到右边；第二步配方，左右两边加上一次项系数一半的平方；第三步左边写成完全平方式；第四步，直接开方即可；（2）形如型，方程两边同时除以二次项系数，即化成，然后配方．将方程的常数项移到右边，含的项移到左边，两边都加上，左边化为完全平方式，右边合并即可得到结果．
【详解】解：，
移项得：，
配方得：，即，
所以▊．
故选：B．
9. 某班六个合作学习小组人数如下：5，6，x，7，7，8．已知这组数据的平均数是6，则这组数据的中位数是（ ）
A. B. 6C. D. 5
【答案】A
【解析】
【分析】本题考查了中位数和平均数的求解，根据题意得求出，可知这组数据为：，即可求出中位数．
【详解】解：由题意得：，
解得：，
∴这组数据为：
故中位数为：，
故选：A
10. 小明在一次野外实践时，发现一种植物的主干长出若干数目的枝干，每个枝干又长出同样数目的小分支．已知1个主干长出的枝干和小分支的总数是30，则这种植物每个枝干长出小分支的个数是（ ）
A. 5B. 6C. 7D. 8
【答案】A
【解析】
【分析】本题考查了一元二次方程的应用．设这种植物每个支干长出的小分支个数是x，根据支干和小分支的总数是30，即可得出关于x的一元二次方程，解方程即可求解．
【详解】解：设这种植物每个支干长出的小分支个数是x，
依题意得：，
整理得：，
解得：，（不合题意，舍去），
∴这种植物每个支干长出的小分支个数是5．
故选：A．
11. 某同学在计算一组数据的方差时，得到了这样一个式子：．以下是四位同学对于这组数据的描述：
甲：这组数据的平均数是7；乙：这组数据的中位数是5；丙：这组数据的众数是6；丁：这组数据的方差是．其中描述错误的同学有（ ）
A. 4位B. 3位C. 2位D. 1位
【答案】D
【解析】
【分析】根据方差计算公式可知，这组数据为5，6，6，8，10，共5个，据此可求出平均数，中位数和众数，再计算出方差即可得到答案．
【详解】解：根据方差计算公式可知，这组数据为5，6，6，8，10，共5个，
∴这组数据的平均数为，中位数为6，众数为6，
∴这组数据的方差为，
∴四个同学中，只有乙同学说法错误，
故选：D．
【点睛】本题主要考查了求平均数，中位数，众数和方差，根据方差计算公式得到这组数据是解题的关键．
12. 关于的一元二次方程的根的情况，叙述正确的是（ ）
A. 方程没有实数根
B. 方程有两个实数根
C. 若直线不经过第三象限，则方程有两个不相等的实数根
D. 若直线不经过第一象限，则方程有两个不相等的实数根
【答案】D
【解析】
【分析】本题考查了一元二次方程根的判别式，一次函数的性质，熟练掌握各知识点是解答本题的关键．求出可判断A和B；由直线不经过第三象限得出可判断C；由直线不经过第一象限得出可判断D．
【详解】解：∵，无法判断的正负，
∴无法判断方程根的情况，故A，B不正确；
C．若直线不经过第三象限，则，
∴无法判断的正负，故C不正确；
D．若直线不经过第一象限，则，
∴，
∴方程有两个不相等的实数根，故D正确．
故选D．
二、填空题（本大题共4个小题，每小题3分，共12分）
13. 某小区共有300户居民，从中随机抽取5户，每户月平均用水是如下（单位：吨）：8，10，10，13，14．由此估计这300户居民每月共用水约为____________吨．
【答案】3300
【解析】
【分析】本题考查了平均数的计算和用样本估计总体的知识，熟知上述计算过程是解题的关键．
用小区户家庭乘以随机抽取的用户的平均月用水量即可．
【详解】解：
（吨），
故答案为：3300．
14. 某公司今年1月份的利润为100万元，3月份的利润上升到144万元，若1至3月利润的增长率相同，则每月增长的百分率是____________．
【答案】
【解析】
【分析】本题考查了一元二次方程的应用．根据题意正确的列方程是解题的关键．设平均每月利润增长的百分率为x，则2月份利润为万元，3月份的利润为万元，然后列方程，计算求出满足要求的解即可．
【详解】解：设平均每月利润增长的百分率为x，
根据题意，得，
解得，（舍去），
∴平均每月利润增长的百分率为．
故答案为：．
15. 已知数据，，…，的方差是3，则一组新数据，，…，的方差是_____________．
【答案】12
【解析】
【分析】本题考查了方差的定义．当数据都加上一个数时，平均数也加上这个数，方差不变，即数据的波动情况不变；当数据都乘以一个数时，平均数也乘以这个数（不为0），方差变为这个数的平方倍．如果一组数据，，…，的方差是，那么数据，，…，的方差是，数据，，…，的方差不变，依此规律即可得出答案．
【详解】解：∵数据，，…，的方差是3，
∴另一组数据，，…，的方差为，
∴，，…，的方差是12．
故答案为：．
16. 已知是关于的一元二次方程的两个实数根．已知等腰三角形的一边长为9，若恰好是另外两边的边长，则另外两边长分别为____________．
【答案】1和9
【解析】
【分析】本题主要考查了一元二次方程根的判别式、等腰三角形的定义、三角形的三边关系等知识点，掌握一元二次根的判别式成为解题的关键．
分9为底边和腰两种情况，分别结合等腰三角形的性质讨论方程的根的情况，并运用三角形的三边关系验证即可．
【详解】解：①当9为底边长时，此时方程有两个相等的实数根，，解得，
方程变为，解得，
，
∴不能构成三角形；
②当9为腰长时，把代入方程得，解得.
当时，方程变为，解得，
，
∴不能组成三角形；
当时，方程变为，解得，能组成三角形.
三角形另外两边长分别为1和9．
故答案为：1和9．
三、解答题（本大题共8个小题，共72分．解答应写出文字说明、证明过程或演算步骤）
17. 用适当的方法解方程：
（1）；
（2）
【答案】（1），；
（2），
【解析】
【分析】（）把右式移到左边，再利用因式分解法解答即可；
（）把右式移到左边，再利用公式法解答即可；
本题考查了解一元二次方程，掌握解一元二次方程的方法是解题的关键．
【小问1详解】
解：移项得，，
∴或，
∴，；
【小问2详解】
解：移项得，，
∵，
∴
∴，
即，．
18. 学校准备组织“走到阳光下”活动，引导学生积极参加体育锻炼，需提前购买一批运动鞋供学生借用，现从各年级随机抽取了部分学生的鞋号，绘制了如图所示的统计图，请根据相关信息，解答下列问题：
（1）图1中的值为____________，并补全条形统计图；
（2）本次调查获取的样本数据的众数为____________，中位数为____________；
（3）根据样本数据，若学校计划购买200双运动鞋，建议购买36号运动鞋多少双？
【答案】（1）；补全图形见解析；
（2）众数为35；中位数；
（3）双
【解析】
【分析】（1）由36号的频数除以其频率可得总人数，再求解35号的人数，再补全图形即可；
（2）找出出现次数最多的即为众数，将数据按照从小到大顺序排列，求出中位数即可；
（3）由200乘以36号的占比，计算即可得到结果．
【小问1详解】
解：本次接受随机抽样调查的学生人数为（人），
，
解得：．
∵，
补全图形如下：
；
【小问2详解】
解：∵在这组样本数据中，35出现了12次，出现次数最多，
∴这组样本数据的众数为35；
∵将这组样本数据从小到大得顺序排列，其中处于中间的两个数都为36，
∴中位数为；
【小问3详解】
解：∵在40名学生中，鞋号为36的学生人数比例为，
∴由样本数据，估计学校各年级中学生鞋号为36的人数比例约为，
则计划购买200双运动鞋，有双为36号．
【点睛】此题考查了中位数和众数，条形统计图，扇形统计图，以及用样本估计总体，弄清题意是解本题的关键．
19. 已知关于的一元二次方程有两个不相等的实数根和．
（1）求实数的取值范围；
（2）当时，求的值．
【答案】（1）；
（2）0
【解析】
【分析】本题考查了一元二次方程根的判别式，一元二次方程根与系数的关系，因式分解法解一元二次方程，熟练掌握各知识点是解答本题的关键．
（1）根据方程的判别式可得关于k的不等式，解不等式即得答案；
（2）由根与系数的关系得，然后把变形为代入计算即可．
【小问1详解】
一元二次方程有两个不相等的实数根，
，
即
；
【小问2详解】
当时，即
，
解得（舍去）
的值为0．
20. 开学初，张明和李强结伴去买学习用品，二人购买三种笔记本的价格和数量如下表：
（1）从平均价格看，二人谁买的笔记本要便宜些？
（2）学期中，张明又分别购买了三种笔记本各1本，请你计算此次购买笔记本的平均价格与他开学初购买时相比是否发生变化；
（3）学期末，李强又购买了三种笔记本共12本，且平均价格与自己开学初购买时相比未发生变化，请你直接写出他学期末购买三种笔记本的数量分别为多少．（写出一种可能的购买情况即可）
【答案】（1）李强买的笔记本要便宜些
（2）此次购买笔记本的平均价格与他开学初购买时相比没有发生变化
（3）购买单价4元的1本，购买单价3元的6本，购买单价2元的5本或购买单价4元的2本，购买单价3元的4本，购买单价2元的6本或购买单价4元的3本，购买单价3元的2本，购买单价2元的7本．（答案不唯一）．
【解析】
【分析】本题考查了平均数，熟练掌握平均数计算方法是解答本题的关键．
（1）根据加权平均数的计算方法分别求出二人所买笔记本的平均价格比较即可；
（2）根据平均数的计算方法计算后判断即可；
（3）根据平均数的计算方法计算即可．
【小问1详解】
解：（元/本）；（元/本）；
，
∴李强买的笔记本要便宜些；
【小问2详解】
解：（元/本）；
此次购买笔记本的平均价格与他开学初购买时相比没有发生变化；
【小问3详解】
解：∵（元/本），
或（元/本），
或（元/本），
∴可以购买单价4元的1本，购买单价3元的6本，购买单价2元的5本或购买单价4元的2本，购买单价3元的4本，购买单价2元的6本或购买单价4元的3本，购买单价3元的2本，购买单价2元的7本．（答案不唯一）．
21. 如图1，有一长方形菜地，长比宽多2米．求菜地的面积．老师在黑板上的板书：．
（1）请根据老师的板书写出的实际意义为_________________；
（2）如图2，经测量菜地的长为12米．王师傅为了扩大菜地面积，向周围开垦荒地，已知四周开垦的菜地宽度均为米，
①则开垦后的菜地面积为________________（结果用含的代数式表示）；
②经测量，菜地开垦后面积为224平方米，求四周开垦的菜地宽度．
【答案】（1）菜地的宽；
（2）①；②四周开垦的菜地宽度为2米
【解析】
【分析】本题考查额一元二次方程的实际应用，多形式与多项式的乘法，灵活运用所学知识是解题关键．
（1）根据题意即可得到答案；
（2）由题意得，开垦后菜地的长为米，菜地的宽为米，即可求出答案；
（3）利用（2）的结论列方程求解即可．
【小问1详解】
解：由题意得：x的实际意义是菜地的宽度；
故答案为：菜地的宽度；
【小问2详解】
解：①∵菜地的长为12米，
∴菜地的宽为10米，
∵四周开垦的菜地宽度均为a米，
∴开垦后菜地的长为米，菜地的宽为米，
∴开垦后菜地的面积为：
，
故答案为：；
②由题意，得
，
解得，（舍去）．
∴四周开垦的菜地宽度为2米．
22. 【新考向】阅读下面的材料，回答问题：
解方程，这是一个一元四次方程，根据该方程的特点，它的解法通常是：
设，那么，于是原方程可变为①，解得．
当时，；
当时，；
原方程有四个根：．
这一方法在由原方程得到方程①的过程中；利用“换元法”达到降次的目的，体现了数学的转化思想．
（1）方程的解为________________________；
（2）仿照材料中的方法，尝试解方程．
【答案】（1），，，
（2），
【解析】
【分析】本题考查了一元二次方程的求解。掌握各类求解方法是解题关键．
（1）设，那么，于是原方程可变为，即可求解；
（2）设，则原方程变为，即可求解；
【小问1详解】
解：设，那么，于是原方程可变为；
解得：；
当时，；
当时，；
原方程有四个根：，，，
故答案为：，，，
【小问2详解】
解：设，则原方程变为，
解得：；
当时，，解得：；
当时，，即
∴方程无实数根
故原方程的解为：
23. [新情境]如图1，是某市三个垃圾存放点，点分别位于点的正北和正东方向，．甲，乙，丙，丁四人分别测得的长度如下表：
他们又调查了各点的垃圾量，并绘制了下列不完整的统计图2和图3．
（1）表中的中位数是__________，长度的平均数__________；
（2）求处垃圾量，并将图2补充完整；
（3）用（1）中的作为的长度，要将A，B两处的垃圾分别沿运到处，已知运送1千克垃圾每米的费用为元，求运送垃圾所需的总费用．
【答案】（1），
（2），条形统计图见解析
（3）元
【解析】
【分析】本题考查了统计数据的求解、条形统计图和扇形统计图信息关联问题以及勾股定理的应用，注意数据处理的准确性即可．
（1）中位数，是按顺序排列的一组数据中居于中间位置的一个数据（或最中间两个数据的平均数）．平均数，是表示一组数据集中趋势的量数，是指在一组数据中所有数据之和再除以这组数据的个数．
（2）根据处的垃圾量的条形统计图和扇形统计图的数据求出垃圾总量即可求解；
（3）计算即可求解；
【小问1详解】
解：将甲，乙，丙，丁四人分别测得的长度按照从大到小的顺序排列为：，
∴表中的中位数是为：；
长度的平均数；
故答案为：，
【小问2详解】
解：由题意得：垃圾总量为：（千克），
∴处的垃圾量为：（千克），
条形统计图如下：
【小问3详解】
解：∵，，
∴，
（元），
∴运送垃圾所需的总费用为元
24. 某商店以20元/千克的单价新进一批商品，经调查发现，在一段时间内，销售量（千克）与销售单价（元/千克）之间的函数关系如图所示．
（1）求与之间的函数关系式；
（2）若该商品的销售单价为50元，求销售利润为多少元？
（3）现要求尽快售完该商品，并使销售利润达到800元，求销售单价应定为每千克多少元？
（4）销售利润能达到1000元吗？若能，求出此时的销售单价；若不能，请说明理由．
【答案】（1）；
（2）销售利润为900元；
（3）销售单价应定为每千克40元；
（4）不能，理由见解析
【解析】
【分析】本题考查了一元二次方程的应用，一次函数的应用，判别式及代入求值，找出数量关系，列出方程和函数解析式是解答本题的关键．
（1）由图知，y与x之间的函数关系分两段，当时，是一个常数；当时，利用待定系数法可以求出函数关系式；
（2）把代入解析式可求出y，根据利润=（销售单价-进价）×销售量可求出销售利润；
（3）根据“销售利润达到800元”可得，解方程即可得出销售单价；
（4）根据销售利润达到1000元可列方程，将该方程化简为一元二次方程的一般形式，根据，可知方程无实数根，从而得到答案．
【小问1详解】
当时，设，将和代入，得，
解得，
与之间的函数关系式为；
【小问2详解】
解：当时，，
（元），
答：销售利润为900元；
【小问3详解】
解：当销售利润达到800元时，即，
解得，
∴要尽快售完该商品，
舍去．
答：销售单价应定为每千克40元；
【小问4详解】
销售利润不能达到1000元．
当销售利润达到1000元时，，
整理得：，
，
∴方程没有实数根，
日期
4月29日
4月30日
5月1日
5月2日
5月3日
5月4日
5月5日
日最高气温
价格（元/本）
4
3
2
合计
张明购买数量
2
2
2
6
李强购买数量
1
2
3
6
甲
乙
丙
丁
（单位：m）
102
99