广东省佛山市八校联考2024-2025学年九年级上学期期中数学试卷

这是一份广东省佛山市八校联考2024-2025学年九年级上学期期中数学试卷，共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1.若nm=57，则nm-n的值为( )
A. 72B. 52C. 57D. -52
2.如果一元二次方程x2+px+q=0能用公式法求解，那么必须满足的条件是( )
A. p2-4q≥0B. p2-4q≤0C. p2-4q>0D. p2-4qBC)，则BCAB=( )
A. ABAC
B. ACBC
C. ABBC
D. AB2AC2
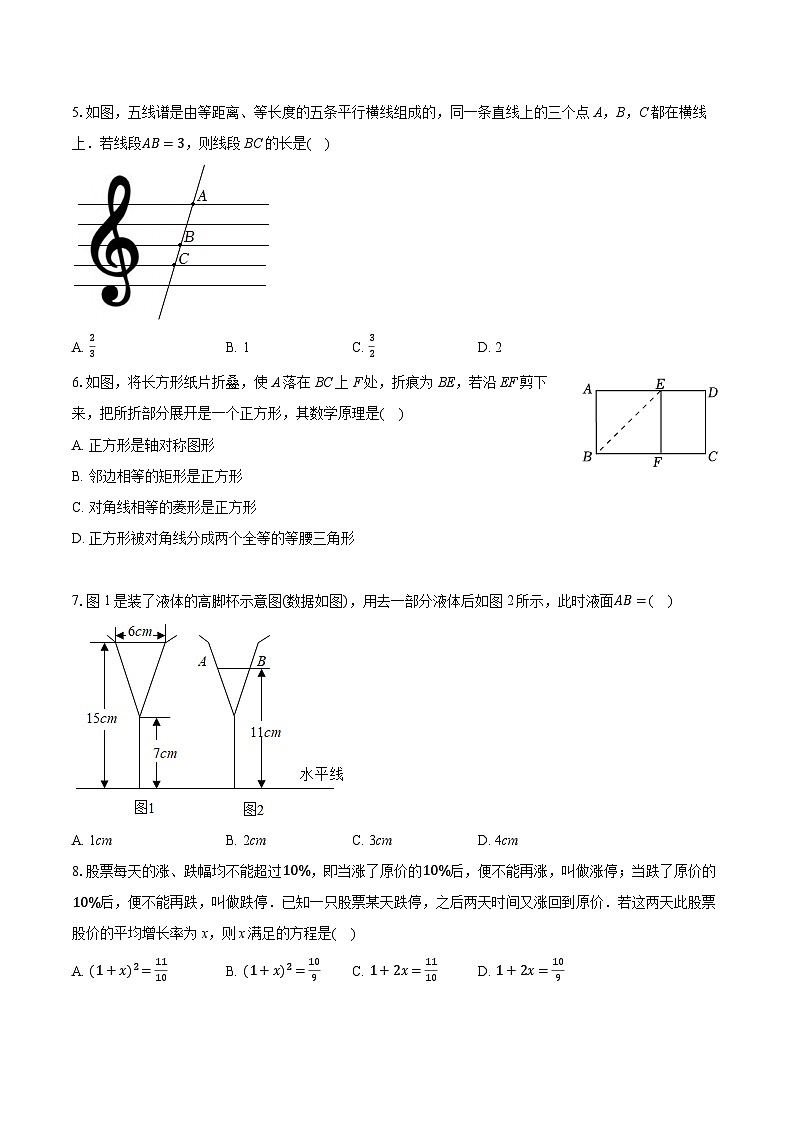
5.如图，五线谱是由等距离、等长度的五条平行横线组成的，同一条直线上的三个点A，B，C都在横线上．若线段AB=3，则线段BC的长是( )
A. 23B. 1C. 32D. 2
6.如图，将长方形纸片折叠，使A落在BC上F处，折痕为BE，若沿EF剪下来，把所折部分展开是一个正方形，其数学原理是( )
A. 正方形是轴对称图形
B. 邻边相等的矩形是正方形
C. 对角线相等的菱形是正方形
D. 正方形被对角线分成两个全等的等腰三角形
7.图1是装了液体的高脚杯示意图(数据如图)，用去一部分液体后如图2所示，此时液面AB=( )
A. 1cmB. 2cmC. 3cmD. 4cm
8.股票每天的涨、跌幅均不能超过10%，即当涨了原价的10%后，便不能再涨，叫做涨停；当跌了原价的10%后，便不能再跌，叫做跌停．已知一只股票某天跌停，之后两天时间又涨回到原价．若这两天此股票股价的平均增长率为x，则x满足的方程是( )
A. (1+x)2=1110B. (1+x)2=109C. 1+2x=1110D. 1+2x=109
9.小明和小红一起做作业，在解一道一元二次方程时，小明在化简过程中写错了常数项，得到两个根分别是2和5；小红在化简过程中写错了一次项系数，得到两个根分别是2和6.则此方程正确的解为( )
A. x1=x2=2B. x1=5，x2=6C. x1=3，x2=4D. 此方程无解
10.如图，在菱形ABCD中，AB=6cm，∠A=60∘，点P从点A出发，以1cm/s的速度沿AB向点B运动，同时，点Q从点C出发，以2cm/s的速度沿CB向点B运动，设点P的运动时间为t s，当△PDQ为等边三角形时，t的值为( )
A. 1
B. 1.3
C. 1.5
D. 2
二、填空题：本题共5小题，每小题3分，共15分。
11.若关于x的一元二次方程(m-1)x2+x+m2-1=0有一个根为0，则m的值是______.
12.如图，在平面直角坐标系内，某图象上的点A、B为整数点，以点O为位似中心将该图象扩大为原的2倍，则点A的坐标为______.
13.四分仪是一种十分古老的测量仪器.其出现可追溯到数学家托勒密的《天文学大成》图1是描述古代测量员用四分仪测量一方井的深度，将四分仪置于方井上的边沿，通过观衡杆测望井底点F、窥衡杆与四分仪的一边BC交于点H.如图2，四分仪为正方形ABCD.方井为矩形BEFG.若测量员从四分仪中读得AB为0.8，BH为0.4实地测得BE为2，则井深BG为______.
14.如图，点E，F是菱形ABCD边AB，BC的中点，BA=BD，EF= 3，则菱形ABCD的面积是______.
15.园林小路，曲径通幽，如图所示，小路由白色的正方形大理石和黑色的三角形大理石密铺而成.已知中间的所有正方形的面积之和是a平方米，内圆的所有三角形的面积之和是b平方米，那么这条小路一共占地______平方米(用含有a和b的式子表示).
三、解答题：本题共8小题，共75分。解答应写出文字说明，证明过程或演算步骤。
16.(本小题7分)
解方程：(x-1)2-2(x-1)=0.
17.(本小题7分)
在△ABC中，∠ABC=90∘
(1)作线段AC的垂直平分线1，交AC于点O；(保留作图痕迹，请标明字母)
(2)连接BO并延长至D，使得OD=OB；连接DA、DC，证明四边形ABCD是矩形．
18.(本小题7分)
某学校准备开设篮球、足球、排球、游泳等4项体育特色课程，为了解学生的参与情况，该校随机抽取了部分学生的报名情况(每人选报一个项目)，小颖根据调查结果绘制了两幅不完整的统计图，请你根据图中信息，解答下列问题：
(1)本次抽样调查的总人数为______人.
(2)扇形统计图中“排球”对应的圆心角的度数为______.若该学校共有学生1200名，请估计参加“游泳”的有______人.
(3)通过初选有4名优秀同学(两男两女)顺利进入了游泳选拔赛，学校将推荐2名同学参加新一轮比赛.请用画树状图或列表法求出参加新一轮比赛的2名同学恰为一男一女的概率.
19.(本小题9分)
我校新城校区新建一个三层停车楼，每一层布局如图所示．已知每层长为50米，宽20米．阴影部分设计为停车位，地面需要喷漆，其余部分是等宽的通道，已知喷漆面积为736平方米．
(1)求通道的宽是多少米？
(2)据调查分析，停车场多余64个车位可以对外出租，当每个车位的月租金为200元时，可全部租出；当每个车位的月租金每上涨10元，就会少租出1个车位，当每个车位的月租金上涨多少元时，既能优惠大众，又能使对外开放的月租金收入为14400元？
20.(本小题9分)
如图，已知G、H分别是四边形ABCD对边AD、BC上的点，AD//BC，直线GH分别交BA和DC的延长线于点E、F.
(1)当S△CFHS四边形CDGH=18时，求CHDG的值；
(2)连接BD交EF于点M，且MG⋅ME=MF⋅MH，求证：四边形ABCD是平行四边形.
21.(本小题9分)
综合与实践
主题：正方形卡纸的裁切与拼接.
素材：大小不等的两张正方形卡纸
步骤1：将大正方形卡纸ABCD和小正方形卡纸BEFG按图
(1)所示的方式摆放(点G在BC上)，用圆规在AB上截取AH=BE，连接DH，HF；
步骤2：首先沿虚线DH，FH裁切卡纸，然后拼接成一个大正方形.
猜想与证明：
(1)△DAH与△HEF是否全等？并证明你的猜想.
迁移与应用：
(2)若大正方形卡纸的边长是小正方形的两倍，将大正方形卡纸对折两次并展开后，按图
(2)所示的方式摆放(虚线为折痕).请你用无刻度的直尺在图
(2)中画出两条裁切线，使裁切后的卡纸可以拼接成一个大正方形.
22.(本小题13分)
如图(1)，正方形ABCD和正方形AEFG，边AE在边AB上，AB=12，AE=6 2，将正方形AEFG绕点A逆时针旋转α(0∘≤α≤45∘).
(1)如图(2)，正方形AEFG旋转到此位置，求证：BE=DG；
(2)在旋转的过程中，当∠BEA=120∘时，试求BE的长；
(3)BE的延长线交直线DG于点P，在旋转的过程中，是否存在某时刻BF=BC？若存在，试求出DP的长；若不存在，请说明理由.
23.(本小题14分)
如图，在平面直角坐标系中，O为原点，平行四边形ABCD的顶点B、C在x轴上，A在y轴上，OA=OC=2OB=4，直线y=x+t(-2≤tBC)，
∴BCAB=ABAC，
故选：A.
根据黄金分割点的定义，列出比例式进行求解即可．
本题考查黄金分割，熟练掌握黄金分割中的比例关系是解题的关键．
5.【答案】C
【解析】【分析】
本题考查的是平行线分线段成比例.过点A作平行横线的垂线，交点B所在的平行横线于D，交点C所在的平行横线于E，根据平行线分线段成比例解答即可.
【解答】
解：过点A作平行横线的垂线，交点B所在的平行横线于D，交点C所在的平行横线于E，
则ABBC=ADDE，即3BC=2，
解得：BC=32.
6.【答案】B
【解析】解：由折叠的性质可知，∠A=∠ABF=∠BFE=90∘，
∴四边形ABFE是矩形，
∵BA=BF，
∴四边形ABFE是正方形(邻边相等的矩形是正方形).
故选：B.
根据邻边相等的矩形是正方形证明即可．
本题考查剪纸问题，正方形的判定等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．
7.【答案】C
【解析】【分析】
本题考查相似三角形的应用，解本题的关键熟练掌握相似三角形的判定与性质．高脚杯前后的两个三角形相似．根据相似三角形的判定和性质即可得出结果．
【解答】
解：如图：过O作OM⊥CD，垂足为M，过O作ON⊥AB，垂足为N，
∵CD//AB，
∴△CDO∽ABO，
即相似比为CDAB，
∴CDAB=OMON，
∵OM=15-7=8，ON=11-7=4，
∴CDAB=OMON，
6AB=84，
∴AB=3，
故选：C.
8.【答案】B
【解析】解：假设股票的原价是1，设平均每天涨x.
则90%(1+x)2=1，
即(1+x)2=109，
故选：B.
股票一次跌停就跌到原来价格的90%，再从90%的基础上涨到原来的价格，且涨幅只能≤10%，所以至少要经过两天的上涨才可以．设平均每天涨x，每天相对于前一天就上涨到1+x.
此题考查增长率的定义及由实际问题抽象出一元二次方程的知识，这道题的关键在于理解：价格上涨x%后是原来价格的(1+x)倍．
9.【答案】C
【解析】解：由题意得：x1+x2=2+5=7，x1x2=12，
A、x1+x2=2+2=4≠7，x1x2=2×2=4≠12，故该选项不符合题意；
B、x1+x2=5+6=11≠7，x1x2=5×6=30≠12，故该选项不符合题意；
C、x1+x2=3+4=7，x1x2=3×4=12，故该选项符合题意；
D、由C分析可知，故该选项不符合题意；
故选：C.
根据题意得出原方程中x1+x2=7，x1x2=12，逐项分析判断，即可求解．
本题考查了一元二次方程根与系数的关系，根据题意得出原方程中x1+x2=7，x1x2=12是解题的关键．
10.【答案】D
【解析】解：如图，延长AB至点M，使BM=AP，连接QM.
∵四边形ABCD是菱形，∠A=60∘，
∴AB=AD，
∴∠APD+∠ADP=120∘，
∵BM=AP，
∴AD=MP，
∵△PDQ为等边三角形，
∴DP=PQ，∠DPQ=60∘，
∴∠MPQ+∠APD=120∘，
∴∠ADP=∠MPQ.
在△ADP和△MPQ中，
AD=MP∠ADP=∠MPQDP=PQ，
∴△ADP≌△MPQ(SAS)，
∴AP=MQ，∠M=∠A=60∘.
又∵BM=AP，
∴△BMQ是等边三角形，
∴BQ=AP.
∵AP=t cm，CQ=2t cm，
∴BC=CQ+BQ=3t cm.
∵BC=6cm.
∴3t=6，
∴t=2.
故选：D.
延长AB至点M，使BM=AP，连接QM，易证△ADP≌△MPQ，即可推出△BMQ是等边三角形，列出方程即可解决问题．
本题考查菱形的性质、等边三角形的判定和性质，解答本题的关键是作出辅助线，构造全等三角形．
11.【答案】-1
【解析】解：把x=0代入(m-1)x2+x+m2-1=0得m2-1=0，解得m1=1，m2=-1，
而m-1≠0，
所以m=-1.
故答案为：-1.
根据一元二次方程的解的定义把x=0代入(m-1)x2+x+m2-1=0得关于m的方程，然后解关于m的方程后利用一元二次方程的定义确定m的值．
本题考查了一元二次方程的解：能使一元二次方程左右两边相等的未知数的值是一元二次方程的解．注意一元二次方程的定义．
12.【答案】(-2,2)或(2,-2)
【解析】解：由题意得：A的坐标为(-1×2,1×2)或(-1×(-2),1×(-2))，
∴A的坐标为(-2,2)或(2,-2)，
故答案为：(-2,2)或(2,-2).
分两种情况讨论，然后根据位似变换的性质计算即可．
本题考查位似变换，坐标与图形性质，解答本题的关键要明确：在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或-k.
13.【答案】3.2
【解析】解：依题意，AB//EF，
∴△ABH∽△FEH，
∴ABEF=BHEH，
∵测量员从四分仪中读得AB为0.8，BH为0.4，实地测得BE为2.
∴0.8EF=0.42-0.4
解得：EF=3.2，
∴BG=3.2，
故答案为：3.2.
根据相似三角形的判定与性质即可解答．
本题考查了相似三角形的应用，能得出△ABH∽△FEH是解题的关键．
14.【答案】2 3
【解析】解：如图，
∵点E，F是菱形ABCD边AB，BC的中点，EF= 3，
∴AC=2EF=2 3，AC⊥BD，AO=12AC= 3，BO=12BD，
∵BA=BD，
∴BO=12AB，
设BO=x，则AB=2x，
∴AO= AB2-BO2= 3x= 3，
∴x=1，
∴BD=2，
∴菱形ABCD的面积是12AC⋅BD=12×2 3×2=2 3，
故答案为：2 3.
如图，记AC、BD的交点为O，由点E，F是菱形ABCD边AB，BC的中点，EF= 3，可得AC=2EF=2 3，AC⊥BD，AO=12AC= 3，BO=12BD，由BA=BD，可得BO=12AB，设BO=x，则AB=2x，由勾股定理得，AO= AB2-BO2= 3x= 3，可求x=1，则BD=2，根据菱形ABCD的面积是12×AC×BD，计算求解即可．
本题考查了中位线，菱形的性质，勾股定理等知识．熟练掌握中位线，菱形的性质，勾股定理是解题的关键．
15.【答案】(a+2b)
【解析】解：过点C作CM⊥BA交BZ的延长线于M，过G作GN⊥AE于N，如图所示：
正方形ABDE和正方形ACFH有公共顶点A，△AEG为内圈三角形，△ABC为外圈三角形，
∴∠M=∠ANG=90∘，
∵∠BAE=90∘，∠CAG=90∘，AB=AE，AC=AG，
∴∠BAC+∠NAG=180∘，
又∵∠BAC+∠MAC=180∘，
∴∠MAC=∠NAG，
在△AMC和△ANG中，
∠M=∠ANG=90∘∠MAC=∠NAGAC=AG，
∴△AMC≌△ANG(AAS)，
∴CM=GN，
∴S△ABC=12AB⋅CM，S△AEG=12AE⋅GN=12AB⋅CM，
∴S△ABC=S△AEG，
同理可证：其它两个公共顶点处正方形的内圈三角形与外圈三角形的面积相等，即每两个公共顶点处正方形的内圈三角形与外圈三角形的面积相等，
∴内圈的所有三角形的面积之和等与外圈的所有三角形的面积之和，
∵内圈的所有三角形的面积之和b平方米，所有正方形的面积之和为a平方米，
∴外圈的所有三角形的面积之和为b平方米，
∴小路的总面积为(a+2b)平方米，
故答案为：(a+2b).
先证明每两个公共顶点处的正方形的内圈三角形的面积于外圈三角形的面积相等，进而可得内圈的所有三角形的面积之和等于外圈的所有三角形的面积之和，据此可得出答案．
本题主要考查了正方形的性质，全等三角形的判定和性质，理解题意，准确识图，熟练掌握正方形的性质，全等三角形的判定和性质是解决问题的关键．
16.【答案】解：(x-1)2-2(x-1)=0，
(x-1)(x-1-2)=0，
∴x-1=0或x-3=0，
∴x1=1，x2=3.
【解析】本题可以运用因式分解法解方程．因式分解法解一元二次方程时，应使方程的左边为两个一次因式相乘，右边为0，再分别使各一次因式等于0即可求解．
根据方程的特点，灵活选择解方程的方法，一般能用因式分解法的要用因式分解法，难以用因式分解法的再用公式法．
17.【答案】(1)解：如图，点O为所作；
(2)证明：∵线段AC的垂直平分线1，
∴OA=OC，
∴OB=OA=OC，
∵OB=OD，
∴OA=OB=OC=OD，
∴四边形ABCD为矩形．
【解析】(1)利用基本作图作AC的垂直平分线得到AC的中点O；
(2)利用直角三角形斜边上的中线得到OB=OA=OC，然后根据对角线互相平分且相等的四边形为矩形可证明四边形ABCD是矩形．
本题考查了作图-基本作图：熟练掌握基本作图(作一条线段等于已知线段；作一个角等于已知角；作已知线段的垂直平分线；作已知角的角平分线；过一点作已知直线的垂线).也考查了矩形的判定．
18.【答案】40 54∘ 420
【解析】解：(1)本次抽样调查的总人数为8÷20%=40(人).
故答案为：40.
(2)参加排球项目的学生人数为40-12-8-14=6(人).
扇形统计图中“排球”对应的圆心角的度数为360∘×640=54∘.
1200×35%=420(人).
∴参加“游泳”的人数大约为420人，
故答案为：54∘，420.
(3)记两名男生分别为A1，A2，两名女生分别为B1，B2，列表如下：
∵由表可知共有12种等可能的结果，其中到市上参加比赛的两人恰为一男一女的结果有8种，
∴到市上参加比赛的两人恰为一男一女的概率为812=23.
(1)用参加足球的学生人数除以其所占的百分比可得本次抽样调查的总人数；
(2)用360∘乘以本次抽样调查中参加排球的学生所占的百分比，即可求出扇形统计图中“排球”对应的圆心角的度数；根据用样本估计总体，用1200乘以扇形统计图中“游泳”对应的百分比，即可得出答案；
(3)画树状图得出所有等可能的结果数以及到市上参加比赛的两人恰为一男一女的结果数，再利用概率公式可得出答案．
本题考查用列表法与树状图法求概率、条形统计图、扇形统计图、用样本估计总体，能够理解条形统计图和扇形统计图，熟练掌握列表法与树状图法以及用样本估计总体是解答本题的关键．
19.【答案】解：(1)设通道的宽是x米，则每一层的停车位可合成长为(50-2x)米，宽为(20-2x)米的长方形，
依题意得：(50-2x)(20-2x)=736，
整理得：x2-35x+66=0，
解得：x1=2，x2=33(不符合题意，舍去).
答：通道的宽是2米．
(2)设每个车位的月租金上涨y元，则每个车位的月租金为(200+y)元，可租出(64-y10)个车位，
依题意得：(200+y)(64-y10)=14400，
整理得：y2-440y+16000=0，
解得：y1=40，y2=400，
又∵要优惠大众，
∴y=40.
答：每个车位的月租金应上涨40元．
【解析】(1)设通道的宽是x米，则每一层的停车位可合成长为(50-2x)米，宽为(20-2x)米的长方形，根据喷漆面积为736平方米(即每一层的停车位的面积为736平方米)，即可得出关于x的一元二次方程，解之取其符合题意的值，即可得出结论；
(2)设每个车位的月租金上涨y元，则每个车位的月租金为(200+y)元，可租出(64-y10)个车位，根据月租金收入为14400元，即可得出关于y的一元二次方程，解之即可得出y的值，再结合要优惠大众，即可得出每个车位的月租金应上涨40元．
本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．
20.【答案】(1)解：已知G、H分别是四边形ABCD对边AD、BC上的点，AD//BC，
∴∠FCH=∠FDG，∠FHC=∠FGD，
∴△FCH∽△FDG，
∴S△CFHS△DFG=(CHDG)2，
∵S△CFHS四边形CDGH=18，
∴S△CFHS△DFG=(CHDG)2=19
∴CHDG=13；
故答案为：13；
(2)证明：连接BD交EF于点M，如图，
已知G、H分别是四边形ABCD对边AD、BC上的点，AD//BC，
∴∠HBM=∠GDM，
∵∠BMH=∠DMG，
∴△BMH∽△DMG，
∴MHMG=MBMD；
∵MG⋅ME=MF⋅MH，
∴MHMG=MEMF，
∴MBMD=MEMF；
∵∠BME=∠DMF，
∴△BME∽△DMF，
∴∠F=∠E，
∴DF//BE，即CD//AB；
∵AD//BC，
∴四边形ABCD是平行四边形．
【解析】(1)由平行条件可得△FCH∽△FDG，由面积的比等于相似比的平方可求得相似比，从而求得结果；
(2)由平行得△BMH∽△DMG，得MHMG=MBMD；再由MG⋅ME=MF⋅MH得MHMG=MEMF，从而得MBMD=MEMF，则△BME∽△DMF，故有∠F=∠E，从而得CD//AB；再由已知即可证明结论成立．
本题考查了相似三角形的判定与性质，平行四边形的判定，熟练掌握相似三角形的判定定理是解题的关键．
21.【答案】解：(1)△DAH与△HEF全等，证明如下：
∵四边形BCD和四边形BEFG都是正方形，
∴AD=AB，∠A=90∘，BE=EF，∠E=90∘，
∵AH=BE，
∴HE=HB+BE=HB+AH=AB，
∴AD=HE，
又∵BE=EF，AH=BE，
∴AH=EF，
在△DAH与△HEF中，
AD=HE，A=∠E=90∘，AH=EF，
∴△DAH≌△HEF(SAS)；
(2)如图2所示：

用用无刻度的直尺画出线段DH，FH，
再沿DH，FH进行裁切，则裁切后的卡纸可以拼接成一个大正方形，理由如下：
由折叠的性质得AH=BH=12AB，
∵大正方形ABCD的边长是小正方形BEFG的2倍，
∴BE=12AB，
∴AH=BE，
∴根据(1)中的拼图的方法即可将图(2)中裁切后的卡纸可以拼接成一个大正方形．
【解析】(1)先证明AD=HE，AH=EF，然后再依据“SAS”判定△DAH与△HEF全等即可；
(2)用用无刻度的直尺画出线段DH，FH，再沿DH，FH进行裁切，则裁切后的卡纸可以拼接成一个大正方形．
此题主要考查了全等三角形的判定与性质，正方形的判定与性质，应用与设计作图，图形的剪拼，准确识图，熟练掌握全等三角形的判定与性质，正方形的判定与性质是解决问题的关键．
22.【答案】(1)证明：∵四边形ABCD和四边形AEFG是正方形，
∴AB=AD，AE=AG，∠BAD=∠EAG=90∘，
∴∠BAE+∠EAD=∠DAG+∠EAD=90∘，
∴∠BAE=∠DAG，
在△ABE和△ADG中，
AB=AD∠BAE=∠DAGAE=AG，
∴△ABE≌△ADG(SAS)，
∴BE=DG；
(2)解：正方形ABCD和正方形AEFG，边AE在边AB上，AB=12，AE=6 2，∠BEA=120∘，如图2，过点A作AH⊥BE交BE的延长线于点H，
∴∠AEH=180∘-∠BEA=60∘，
∵AH⊥BE，即∠AHE=90∘，
∴∠EAH=90∘-60∘=30∘，
∴EH=12AE=12×6 2=3 2，
∴AH= AE2-EH2= (6 2)2-(3 2)2=3 6，
在Rt△ABH中，BH= AB2-AH2= 122-(3 6)2=3 10，
∴BE=BH-EH=3 10-3 2；
(3)解：在旋转的过程中，存在某时刻BF=BC；理由如下：
如图3，连接AF，
∵四边形AEFG是正方形，
∴AE=EF=6 2，∠AEF=90∘，
在直角三角形AEF中，由勾股定理得：
AF= AE2+EF2= (6 2)2+(6 2)2=12，
∵BF=BC=AB=12，
∴AF=BF=AB=12，
∴△ABF是等边三角形，
∵BA=BF，EA=EF，
∴BE是线段AF的垂直平分线，如图，
∵EG是线段AF的垂直平分线，
∴直线BE与直线EG是同一条直线，
∴点P与点G重合，即DP=DG，
设EG与AF交于点O，则AO=EO=12AF=6，∠AOB=90∘，
在直角三角形ABO中，由勾股定理得：BO= AB2-AO2= 122-62=6 3，
∴BE=BO-EO=6 3-6，
∵∠BAE+∠EAD=∠DAG+∠EAD=90∘，
∴∠BAE=∠DAG，
在△ABE和△ADG中，
AB=AD∠BAE=∠DAGAE=AG，
∴△ABE≌△ADG(SAS)，
∴DG=BE，
∴DP=BE=6 3-6.
【解析】(1)结合正方形的性质证明△ABE≌△ADG，由全等三角形的性质可证明BE=DG；
(2)过点A作AH⊥BE交BE的延长线于点H，结合题意可得∠AEH=60∘，进而可得∠EAH=30∘，由“直角三角形中30度角所对的直角边等于斜边的一半”可知EH=12AE=3 2，进而解得AH的长度，再在Rt△ABH中由勾股定理解得，BH的值，即可获得答案；
(3)连接AF，首先证明△ABF是等边三角形，BE是线段AF的垂直平分线，结合EG是线段AF的垂直平分线，易得直线BE与直线EG是同一条直线，即点P与点G重合，设EG与AF交于点O，解得BO，BE的长度，再证明△ABE≌△ADG，由全等三角形的性质可证明BE=DG，即可获得答案．
本题主要考查了正方形的性质、旋转的性质、勾股定理、含30度角的直角三角形的性质、全等三角形的判定与性质、垂直平分线的判定与性质等知识，熟练掌握正方形的性质和全等三角形的性质是解题关键．
23.【答案】(1)证明：由OA=OC=2OB=4知，OC=4，OB=2，
则AD=BC=6，
则点A、B的坐标分别为：(0,4)、(-2,0)，
当y=4时，y=x+t=4，
则x=4-t=4-1=3=12AD，
即点P(3,4)，
即AP=DP；
(2)解：PQ=2 2AP，理由如下：
由点A、B的坐标得，直线AB的表达式为：y=2x+4，
联立上式和y=x+t得：2x+4=x+t，
解得：x=4-t，
即点Q(t-4,2t-4)，
同理可得，点P(4-t,4)，
则AP=4-t，
由点PQ的坐标得，PQ=2 2(4-t)=2 2AP；
(3)解：在x轴上存在点M，使得∠PMQ=90∘，且以点M、P、Q为顶点的三角形与△AOB相似；理由如下：
过点P作PH⊥x轴于点H，过点Q作QI⊥x轴于点I，见图1、2、3，
设点M(m,0)，
由(2)知，点P、Q的坐标分别为：(4-t,4)、(t-4,2t-4)，
则PH=|m-4+t|，HM=OA=4，QI=|m-t+4|，IM=4-2t，
∵∠PMH+∠QMI=90∘，∠QMI+∠IQM=90∘，
∴∠IQM=∠PMH，
∴Rt△PHM∽Rt△MIQ，
∵以点M、P、Q为顶点的三角形与△AOB相似，
则PM：QM=2或12，
故Rt△PHM和Rt△QMI的相似比为：2或12，
则PH：MI=HM：QI=2或12，
当m>0时，如图1，2，
当相似比为2时，如图1，
PHMI=MHQI=2，
则PH=2MI，MH=2QI，
即4=2(m-t+4)且4-t-m=2(2t-4)，
解得：m=13，t=73，
即点M(13,0)，t=73；
当相似比为12时，如图2，
PHMI=MHQI=12，
则PH=12MI，MH=12QI，
则2×4=m-(t-4)且2(m-4+t)=4-2t，
解得：m=143，t=23，
则点M(143,0)，t=23；
当m