上海市虹口区新复兴中学2024—2025学年上学期期中考试九年级数学试卷

这是一份上海市虹口区新复兴中学2024—2025学年上学期期中考试九年级数学试卷，共25页。试卷主要包含了已知两个相似三角形的相似比是4等内容，欢迎下载使用。
1．（4分）下列图形一定是相似图形的是（ ）
A．两个矩形B．两个等腰三角形
C．两个直角三角形D．两个正方形
2．（4分）下列各组中的四条线段（单位：厘米）成比例线段的是（ ）
A．1、2、3、4B．2、3、4、6C．4、5、5、6D．1、2、5、20
3．（4分）如图：在△ABC中，点D、E分别在AB、AC上，根据下列给定的条件，不能判断DE与BC平行的是（ ）
A．B．C．D．
4．（4分）如图，在Rt△ABC中，∠C＝90°，BC＝4，AC＝2，则tanA等于（ ）
A．B．2C．D．
5．（4分）已知、、都是非零向量．下列条件中，不能判定∥的是（ ）
A．||＝||B．＝3C．∥，∥D．＝2，＝﹣2
6．（4分）如图，在▱ABCD中，点E是边AD的中点，EC交对角线BD于点F，如果S△DEF＝3，那么▱ABCD的面积为（ ）
A．6B．12C．24D．36
二.填空题（共12小题，满分48分，每小题4分）
7．（4分）已知x：y＝5：2，那么（x+y）：y＝ ．
8．（4分）已知线段a＝4厘米，c＝9厘米，那么线段a和c的比例中项是 厘米．
9．（4分）点P是线段AB的黄金分割点（AP＞BP），AB＝2，那么线段AP的长是 ．
10．（4分）已知两个相似三角形的相似比是4：9，那么它们对应的角平分线之比是 ．
11．（4分）若向量与单位向量的方向相反，且||＝2，则＝ ．（用表示）
12．（4分）计算：3﹣（2﹣4）＝ ．
13．（4分）如图，已知AB∥CD∥EF，若AC＝6，CE＝3，DF＝2，则BD的长为 ．
14．（4分）在△ABC中，∠C＝90°，如果BC＝3，tanA＝，那么AC＝ ．
15．（4分）如图，在Rt△ABC中，∠ACB＝90°，D是△ABC的重心，若CD＝2，则AB＝ ．
16．（4分）如图，在梯形ABCD中，AD∥BC，AD＝3，BC＝6，点E、F分别在AB、DC上，EF∥BC，如果AE：EB＝1：2，则EF＝ ．
17．（4分）如图所示，在正方形网格上有6个斜三角形，①△ABC，②△BCD，③△BDE，④△BFG，⑤△FGH，⑥△EFK，在②～⑥中，与三角形①相似的有 （填序号）
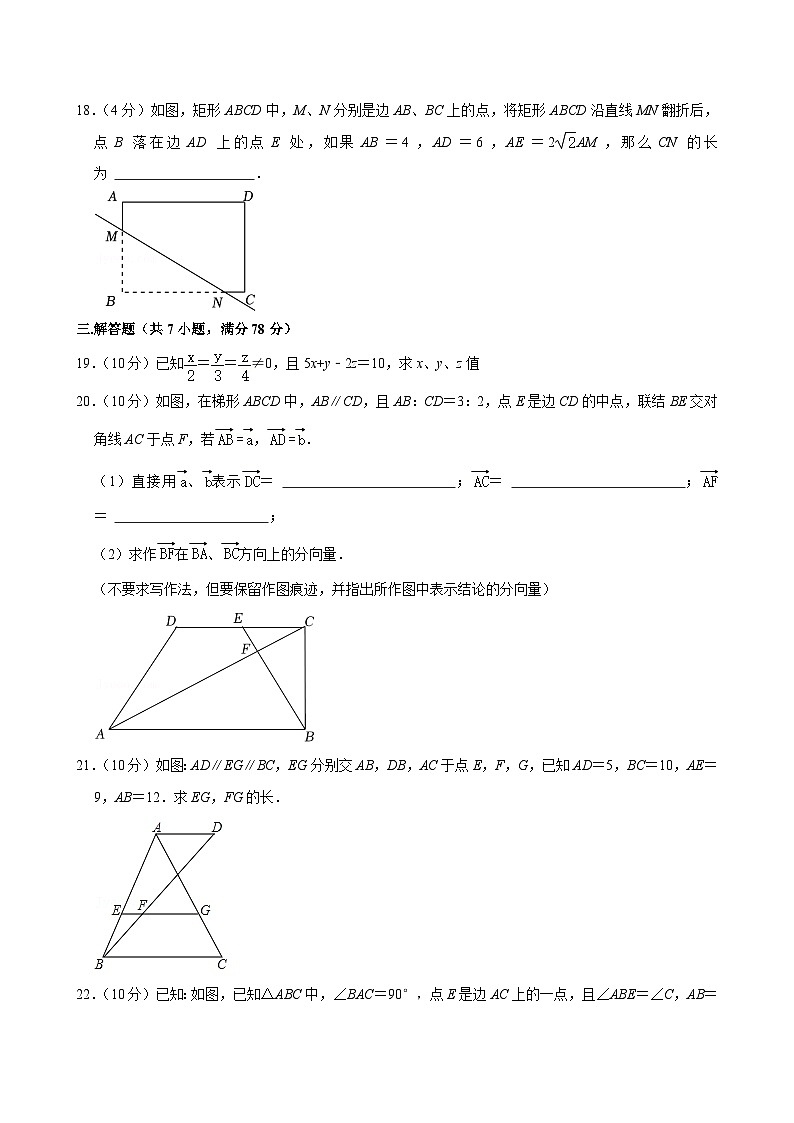
18．（4分）如图，矩形ABCD中，M、N分别是边AB、BC上的点，将矩形ABCD沿直线MN翻折后，点B落在边AD上的点E处，如果AB＝4，AD＝6，AE＝2AM，那么CN的长为 ．
三.解答题（共7小题，满分78分）
19．（10分）已知＝＝≠0，且5x+y﹣2z＝10，求x、y、z值
20．（10分）如图，在梯形ABCD中，AB∥CD，且AB：CD＝3：2，点E是边CD的中点，联结BE交对角线AC于点F，若，．
（1）直接用、表示＝ ；＝ ；＝ ；
（2）求作在、方向上的分向量．
（不要求写作法，但要保留作图痕迹，并指出所作图中表示结论的分向量）
21．（10分）如图：AD∥EG∥BC，EG分别交AB，DB，AC于点E，F，G，已知AD＝5，BC＝10，AE＝9，AB＝12．求EG，FG的长．
22．（10分）已知：如图，已知△ABC中，∠BAC＝90°，点E是边AC上的一点，且∠ABE＝∠C，AB＝3，AC＝4．
（1）求：BE的长；
（2）作ED⊥BC，求：∠EBC的正弦值．
23．（12分）如图，梯形ABCD中，AD∥BC，点E是边AD的中点，连接BE并延长交CD的延长线于点F，交AC于点G．
（1）若FD＝2，，求线段DC的长；
（2）求证：EF•GB＝BF•GE．
24．（12分）学习了相似三角形知识后，小丽同学准备用自制的直角三角形纸板测量校园内一棵古树的高度．已知三角形纸板的斜边长为0.5米，较短的直角边长为0.3米．
（1）小丽先调整自己的位置至点P，将直角三角形纸板的三个顶点位置记为A、B、C（如图①），斜边AB平行于地面MN（点M、P、E、N在一直线上），且点D在边AC（较长直角边）的延长线上，此时测得边AB距离地面的高度EF为1.5米，小丽与古树的距离AF为16米，求古树的高度DE；
（2）为了尝试不同的思路，小丽又向前移动自己的位置至点Q，将直角三角形纸板的三个顶点的新位置记为A′、B′、C′（如图②），使直角边B′C′（较短直角边）平行于地面MN（点M、Q、E、N在一直线上），点D在斜边B′A′的延长线上，且测得此时边B′C′距离地面的高度依然是1.5米，那么小丽向前移动了多少米？
25．（14分）如图，正方形ABCD中，AB＝6，E是边BC上一点（点E不与点B、C重合），点F在CD的延长线上，且BE＝DF，联结EF，分别交AD、AC于点M、N．
（1）已知MD＝1，求BE的长；
（2）求证：EF2＝2EM•FN；
（3）当△AMN是等腰三角形时，求S△AMN的值．
2024-2025学年上海市虹口区九年级（上）期中数学试卷（1）
参考答案与试题解析
一.选择题（共6小题，满分24分，每小题4分）
1．（4分）下列图形一定是相似图形的是（ ）
A．两个矩形B．两个等腰三角形
C．两个直角三角形D．两个正方形
【答案】D
【分析】根据相似图形的定义，结合选项，用排除法求解．
【解答】解：A、两个矩形，对应角相等，对应边不一定成比例，故不符合题意；
B、两个等腰三角形顶角不一定相等，故不符合题意．
C、两个直角三角形，只有一个直角相同，锐角不一定相等，故不符合题意；
D、两个正方形，形状相同，大小不一定相同，符合相似性定义，故符合题意；
故选：D．
【点评】本题考查相似形的定义，熟悉各种图形的性质是解题的关键．
2．（4分）下列各组中的四条线段（单位：厘米）成比例线段的是（ ）
A．1、2、3、4B．2、3、4、6C．4、5、5、6D．1、2、5、20
【答案】B
【分析】根据比例线段的概念，让最小的和最大的相乘，另外两条相乘，看它们的积是否相等即可得出答案．
【解答】解：A、4×1≠2×3，故本选项不符合题意；
B、2×6＝3×4，故本选项符合题意；
C、4×6≠5×5，故本选项不符合题意；
D、1×20≠2×5，故本选项不符合题意；
故选：B．
【点评】本题主要考查了成比例线段的定义，熟练掌握对于给定的四条线段，如果其中两条线段的长度之比等于另外两条线段的长度之比，则这四条线段叫做成比例线段是解题的关键．
3．（4分）如图：在△ABC中，点D、E分别在AB、AC上，根据下列给定的条件，不能判断DE与BC平行的是（ ）
A．B．C．D．
【答案】D
【分析】根据平行线分线段成比例定理的逆定理，即“三条直线被两条直线所截，如果截得的对应线段成比例，那么三条直线平行”，进行分析判断即可．
【解答】解：∵，∴DE∥BC，A不合题意；
∵，∴DE∥BC，B不合题意；
∵，∴DE∥BC，C不合题意；
，不能判断DE与BC平行，D符合题意；
故选：D．
【点评】本题考查的是平行线分线段成比例定理的逆定理，即“三条直线被两条直线所截，如果截得的对应线段成比例，那么三条直线平行”．
4．（4分）如图，在Rt△ABC中，∠C＝90°，BC＝4，AC＝2，则tanA等于（ ）
A．B．2C．D．
【答案】B
【分析】根据正切的定义计算，得到答案．
【解答】解：在Rt△ABC中，∠C＝90°，
∴tanA＝＝2，
故选：B．
【点评】本题考查的是锐角三角函数的定义，掌握锐角A的对边a与邻边b的比叫做∠A的正切是解题的关键．
5．（4分）已知、、都是非零向量．下列条件中，不能判定∥的是（ ）
A．||＝||B．＝3C．∥，∥D．＝2，＝﹣2
【答案】A
【分析】根据平行向量的定义（两个向量方向相同或相反，即为平行向量）分析求解即可求得答案．
【解答】解：A、||＝||只能说明与的模相等，不能判定∥，故本选项符合题意．
B、＝3说明与的方向相同，能判定∥，故本选项不符合题意．
C、∥，∥，能判定∥，故本选项不符合题意．
D、＝2，＝﹣2说明与的方向相反，能判定∥，故本选项不符合题意．
故选：A．
【点评】此题考查了平面向量的知识．此题难度不大，注意掌握平行向量与向量的模的定义是解此题的关键．
6．（4分）如图，在▱ABCD中，点E是边AD的中点，EC交对角线BD于点F，如果S△DEF＝3，那么▱ABCD的面积为（ ）
A．6B．12C．24D．36
【答案】D
【分析】先证明△EFD∽△CFB，依据相似三角形的性质得到△BFC的面积为12，设△DFC的面积为x，然后依据△EDC的面积等于△BCD的面积的一半列方程求得△FCD的面积，从而得到△BCD的面积，最后依据S▱ABCD＝2S△BCD求解即可．
【解答】解：∵ABCD为平行四边形，
∴AD∥BC．
∴△EFD∽△CFB．
又∵E是AD的中点，
∴DE＝CB．
∴S△BCF＝4S△EDF＝12．
设S△DFC＝x，则3+x＝（12+x），
解得：x＝6．
∴S△BCD＝12+6＝18．
∴S▱ABCD＝2S△BCD＝36．
故选：D．
【点评】本题主要考查的是平行四边形的性质、相似三角形的性质和判定，熟练掌握相似三角形的性质和判定定理是解题的关键．
二.填空题（共12小题，满分48分，每小题4分）
7．（4分）已知x：y＝5：2，那么（x+y）：y＝ 7：2 ．
【答案】见试题解答内容
【分析】根据合比性质，可得答案．
【解答】解：由合比性质，得（x+y）：y＝7：2，
故答案为：7：2．
【点评】本题考查了比例的性质，利用了合比性质：＝⇒＝．
8．（4分）已知线段a＝4厘米，c＝9厘米，那么线段a和c的比例中项是 6 厘米．
【答案】6．
【分析】根据比例中项的定义得到a：b＝b：c，然后利用比例性质计算即可．
【解答】解：∵线段a和c的比例中项为b，
∴a：b＝b：c，
即4：b＝b：9，
∴b＝±6（负值舍去）．
故答案为：6．
【点评】本题考查了比例线段：对于四条线段a、b、c、d，如果其中两条线段的比（即它们的长度比）与另两条线段的比相等，如 a：b＝c：d（即ad＝bc），我们就说这四条线段是成比例线段，简称比例线段．判定四条线段是否成比例，只要把四条线段按大小顺序排列好，判断前两条线段之比与后两条线段之比是否相等即可．
9．（4分）点P是线段AB的黄金分割点（AP＞BP），AB＝2，那么线段AP的长是 ﹣1 ．
【答案】﹣1．
【分析】根据黄金分割的定义进行计算，即可解答．
【解答】解：∵点P是线段AB的黄金分割点（AP＞BP），AB＝2，
∴AP＝AB＝×2＝﹣1，
故答案为：﹣1．
【点评】本题考查了黄金分割，熟练掌握黄金分割的定义是解题的关键．
10．（4分）已知两个相似三角形的相似比是4：9，那么它们对应的角平分线之比是 4：9 ．
【答案】见试题解答内容
【分析】直接根据相似三角形的性质即可得出结论．
【解答】解：∵两个相似三角形的相似比是4：9，
∴它们对应的角平分线之比是4：9．
故答案为：4：9．
【点评】本题考查的是相似三角形的性质，熟知相似三角形对应角平分线的比等于相似比是解答此题的关键．
11．（4分）若向量与单位向量的方向相反，且||＝2，则＝ ﹣2 ．（用表示）
【答案】见试题解答内容
【分析】根据向量的表示方法可直接进行解答．
【解答】解：∵向量与单位向量的方向相反，且||＝2，
∴＝﹣2．
故答案为：﹣2．
【点评】本题考查的是平面向量的知识，即长度不为0的向量叫做非零向量，向量包括长度及方向，而长度等于1个单位长度的向量叫做单位向量，注意单位向量只规定大小没规定方向．
12．（4分）计算：3﹣（2﹣4）＝ 2+2 ．
【答案】见试题解答内容
【分析】先利用乘法结合律取括号，然后合并同类项．
【解答】解：原式＝3﹣+2＝2+2．
故答案为：2+2．
【点评】本题主要考查了平面向量，实数的运算法则同样应用于平面向量的计算．
13．（4分）如图，已知AB∥CD∥EF，若AC＝6，CE＝3，DF＝2，则BD的长为 4 ．
【答案】4．
【分析】根据平行线分线段成比例定理列出比例式，把已知数据代入计算即可．
【解答】解：∵AB∥CD∥EF，
∴＝，
∵AC＝6，CE＝3，DF＝2，
∴＝，
解得：BD＝4，
故答案为：4．
【点评】本题考查的是平行线分线段成比例定理，灵活运用定理、找准对应关系是解题的关键．
14．（4分）在△ABC中，∠C＝90°，如果BC＝3，tanA＝，那么AC＝ ．
【答案】见试题解答内容
【分析】根据tanA＝，于是得到＝，即可求出AC．
【解答】解：在△ABC中，∠C＝90°，BC＝3，
∵tanA＝＝，
∴AC＝，
故答案为：．
【点评】本题考查了解直角三角形，涉及的知识有：锐角三角函数定义，利用了方程的思想，熟练掌握定义及定理是解本题的关键．
15．（4分）如图，在Rt△ABC中，∠ACB＝90°，D是△ABC的重心，若CD＝2，则AB＝ 6 ．
【答案】6．
【分析】延长CD交AB于E，如图，根据三角形重心的定义和性质得到CE为斜边AB上的中线，CD＝2DE，则可求出CE，然后根据直角三角形斜边上的中线性质确定AB的长．
【解答】解：延长CD交AB于E，如图，
∵点D是△ABC的重心，
∴CE为斜边AB上的中线，CD＝2DE，
∴DE＝CD＝1，
∴CE＝CD+DG＝2+1＝3，
∴AB＝2CE＝6．
故答案为：6．
【点评】本题考查了三角形的重心：重心到顶点的距离与重心到对边中点的距离之比为2：1．
16．（4分）如图，在梯形ABCD中，AD∥BC，AD＝3，BC＝6，点E、F分别在AB、DC上，EF∥BC，如果AE：EB＝1：2，则EF＝ 4 ．
【答案】见试题解答内容
【分析】作DH∥AB，交BC于H，交EF于G，则四边形ABHD、四边形AEGD都是平行四边形，得出EG＝AD＝BH＝3，CH＝BC﹣BH＝3，由平行线分线段成比例得出＝＝，得出＝，由平行线得出△DFG∽△DCH，得出＝＝，求出FG＝CH＝1，即可得出答案．
【解答】解：作DH∥AB，交BC于H，交EF于G，如图所示：
则四边形ABHD、四边形AEGD都是平行四边形，
∴EG＝AD＝BH＝3，∴CH＝BC﹣BH＝3，
∵AD∥BC，EF∥BC，
∴AD∥EF∥BC，
∴＝＝，
∴＝，
∵EF∥BC，
∴△DFG∽△DCH，
∴＝＝，
∴FG＝CH＝1，
∴EF＝EG+FG＝3+1＝4；
故答案为：4．
【点评】此题考查了相似三角形的判定与性质、平行四边形的判定与性质、平行线分线段成比例定理等知识；证明三角形相似是解题的关键．
17．（4分）如图所示，在正方形网格上有6个斜三角形，①△ABC，②△BCD，③△BDE，④△BFG，⑤△FGH，⑥△EFK，在②～⑥中，与三角形①相似的有 ③④⑤ （填序号）
【答案】见试题解答内容
【分析】两三角形三条边对应成比例，两三角形相似，据此即可解答．
【解答】解：设每个小正方形的边长为1，则△ABC的各边长分别为1、、．则
②△BCD的各边长分别为1、、2；
③△BDE的各边长分别为2、2、2（为△ABC各边长的2倍）；
④△BFG的各边长分别为5、、（为△ABC各边长的倍）；
⑤△FGH的各边长分别为2、、（为△ABC各边长的倍）；
⑥△EFK的各边长分别为3、、．
根据三组对应边的比相等的两个三角形相似得到与三角形①相似的是③④⑤．
故答案为③④⑤．
【点评】此题考查了相似三角形的判定，勾股定理，掌握三组对应边的比相等的两个三角形相似是解题的关键．
18．（4分）如图，矩形ABCD中，M、N分别是边AB、BC上的点，将矩形ABCD沿直线MN翻折后，点B落在边AD上的点E处，如果AB＝4，AD＝6，AE＝2AM，那么CN的长为 6﹣3 ．
【答案】6﹣3．
【分析】如图，过点N作NH⊥AD，可证四边形DCNH是矩形，可得HD＝CN，CD＝NH＝6，由折叠的性质可求EN＝BN＝8﹣CN，EM＝BM，由勾股定理可求AM的长，可得AE的长，EH的长，再由勾股定理可求解．
【解答】解：如图，过点N作NH⊥AD，
∵四边形ABCD是矩形，
∴AB＝CD＝4，∠D＝∠C＝90°，且NH⊥AD，
∴四边形DCNH是矩形，
∴HD＝CN，CD＝NH＝4，
∵将矩形ABCD沿直线MN翻折后，
∴EN＝BN＝6﹣CN，EM＝BM，
∵EM2＝AM2+AE2，
∴（4﹣AM）2＝AM2+8AM2，
∴AM＝1（负值舍去），
∴AE＝2，
∴EH＝AD﹣AE﹣DH＝6﹣2﹣CN，
∵EN2＝HN2+EH2，
∴（6﹣CN）2＝16+（6﹣2﹣CN）2，
∴CN＝6﹣3，
故答案为：6﹣3．
【点评】本题考查了翻折变换，矩形的性质，勾股定理等知识，求出AE的长是本题的关键．
三.解答题（共7小题，满分78分）
19．（10分）已知＝＝≠0，且5x+y﹣2z＝10，求x、y、z值
【答案】见试题解答内容
【分析】首先设x＝2a，y＝3a，z＝4a，然后再代入5x+y﹣2z＝10，可得a的值，进而可得答案．
【解答】解：设x＝2a，y＝3a，z＝4a，
∵5x+y﹣2z＝10，
∴10a+3a﹣8a＝10，
5a＝10，
a＝2，
∴x＝4，y＝6，z＝8．
【点评】此题主要考查了比例的性质，关键是掌握用同一未知数表示各未知数．
20．（10分）如图，在梯形ABCD中，AB∥CD，且AB：CD＝3：2，点E是边CD的中点，联结BE交对角线AC于点F，若，．
（1）直接用、表示＝ ；＝ + ；＝ + ；
（2）求作在、方向上的分向量．
（不要求写作法，但要保留作图痕迹，并指出所作图中表示结论的分向量）
【答案】（1）：，+，+．
（2）见解析．
【分析】（1）利用平行向量的性质求出，再利用三角形法则求出，；
（2）利用平行四边形法则画出向量即可．
【解答】解：（1）∵AB∥CD，AB：CD＝3：2，
∴CD＝AB，
∵＝，∴＝，＝+＝+，
∵E是CD的中点，
∴EC：AB＝1：3，
∵EC∥AB，
∴AF：FC；AB：CE＝3：1，
∴AF＝AC，
∴＝（+）＝+．
故答案为：，+，+．
（2）如图，，即为所求．
【点评】本题考查相似三角形的判定和性质，梯形，平面向量，作图﹣复杂作图等知识，解题的关键是掌握三角形法则．
21．（10分）如图：AD∥EG∥BC，EG分别交AB，DB，AC于点E，F，G，已知AD＝5，BC＝10，AE＝9，AB＝12．求EG，FG的长．
【答案】，．
【分析】在△ABC中，根据平行线分线段成比例求出EG，在△BAD中，根据平行线分线段成比例求出EF，即可求出FG＝EG﹣EF．
【解答】解：∵△ABC中，EG∥BC，
∴△AEG∽△ABC，
∴，
∵BC＝10，AE＝9，AB＝12，
∴＝，
∴EG＝，
∵△BAD中，EF∥AD，
∴＝，
∵AD＝5，AE＝9，AB＝12，
∴＝，
∴EF＝．
∴FG＝EG﹣EF＝﹣＝．
【点评】本题考查了平行线分线段成比例，平行于三角形一边的直线截其他两边（或两边的延长线），所得的对应线段成比例．
22．（10分）已知：如图，已知△ABC中，∠BAC＝90°，点E是边AC上的一点，且∠ABE＝∠C，AB＝3，AC＝4．
（1）求：BE的长；
（2）作ED⊥BC，求：∠EBC的正弦值．
【答案】（1）；
（2）．
【分析】（1）根据勾股定理求出BC＝5，再根据“两角对应相等的两个三角形相似”推出△ABE∽△ACB，再根据相似三角形的性质求解即可；
（2）根据“两角对应相等的两个三角形相似”推出△CED∽△CBA，根据相似三角形的性质求出，CD＝，DE＝，再解直角三角形求解即可．
【解答】解：（1）∵AB＝3，AC＝4，∠A＝90°，
∴，
∵∠A＝∠A，∠ABE＝∠C，
∴△ABE∽△ACB，
∴＝，
∴，
∴；
（2）如图，
∵△ABE∽△ACB，
∴，
∴＝，
∴，
∴，
∵∠A＝∠EDC＝90°，∠C＝∠C，
∴△CED∽△CBA，
∴＝＝，
∴＝＝，
∴CD＝，DE＝，
∴BD＝BC﹣CD＝，
在Rt△ABE中，BE＝＝＝，
∴∠EBC的正弦值＝＝＝．
【点评】此题考查了相似三角形的判定与性质、解直角三角形，熟记相似三角形的判定与性质是解题的关键．
23．（12分）如图，梯形ABCD中，AD∥BC，点E是边AD的中点，连接BE并延长交CD的延长线于点F，交AC于点G．
（1）若FD＝2，，求线段DC的长；
（2）求证：EF•GB＝BF•GE．
【答案】见试题解答内容
【分析】（1）由平行线得出△DEF∽△CBF，得出对应边成比例求出FC，即可得出DC的长；
（2）由平行线得出△DEF∽△CBF，△AEG∽△CBG，得出对应边成比例＝，＝，由已知条件得出AE＝DE，因此＝，即可得出结论．
【解答】解：（1）∵AD∥BC，
∴△DEF∽△CBF，
∴＝＝，
∴FC＝3FD＝6，
∴DC＝FC﹣FD＝4；
（2）证明：∵AD∥BC，
∴△DEF∽△CBF，△AEG∽△CBG，
∴＝，＝，
∵点E是边AD的中点，
∴AE＝DE，
∴＝，
∴EF•GB＝BF•GE．
【点评】本题考查了梯形的性质、相似三角形的判定与性质；熟练掌握梯形的性质，证明三角形相似得出比例式是解决问题的关键．
24．（12分）学习了相似三角形知识后，小丽同学准备用自制的直角三角形纸板测量校园内一棵古树的高度．已知三角形纸板的斜边长为0.5米，较短的直角边长为0.3米．
（1）小丽先调整自己的位置至点P，将直角三角形纸板的三个顶点位置记为A、B、C（如图①），斜边AB平行于地面MN（点M、P、E、N在一直线上），且点D在边AC（较长直角边）的延长线上，此时测得边AB距离地面的高度EF为1.5米，小丽与古树的距离AF为16米，求古树的高度DE；
（2）为了尝试不同的思路，小丽又向前移动自己的位置至点Q，将直角三角形纸板的三个顶点的新位置记为A′、B′、C′（如图②），使直角边B′C′（较短直角边）平行于地面MN（点M、Q、E、N在一直线上），点D在斜边B′A′的延长线上，且测得此时边B′C′距离地面的高度依然是1.5米，那么小丽向前移动了多少米？
【答案】（1）13.5米；
（2）7米．
【分析】（1）先在Rt△ABC中，由勾股定理求得AC，再利用Rt△ABC和Rt△ADF相似求得DF的长，加上EF，即可求得树高DE；
（2）利用Rt△A′B′C′和Rt△D′B′F相似求得B′F的长，即可求得小丽向前移动了多少米．
【解答】解：（1）∵∠DFA＝∠ACB＝90°，∠DAF＝∠CAB，
∴△DFA∽△BCA，
∴＝，
在Rt△ABC中，
∵AB＝0.5m，BC＝0.3m，
由勾股定理得AC＝＝0.4（m），
∵AF＝16m，
∴＝，
∴DF＝12（m），
∴DE＝DF+EF＝12+1.5＝13.5（m），
答：古树的高度DE为13.5米；
（2）∵∠D′FB′＝∠A′C′B′＝90°，∠D′B′F＝∠A′B′C′，
∴△D′FB′∽△A′C′B′，
∴＝，
∴＝，
∴B′F＝9（m），
∴16﹣9＝7（m），
答：小丽向前移动了7米．
【点评】本题考查了相似三角形的应用和勾股定理的应用，解题的关键是证得△DFA∽△BCA和△D′FB′∽△A′C′B′．
25．（14分）如图，正方形ABCD中，AB＝6，E是边BC上一点（点E不与点B、C重合），点F在CD的延长线上，且BE＝DF，联结EF，分别交AD、AC于点M、N．
（1）已知MD＝1，求BE的长；
（2）求证：EF2＝2EM•FN；
（3）当△AMN是等腰三角形时，求S△AMN的值．
【答案】（1）2或3；
（2）证明过程详见解答；
（3）108﹣144．
【分析】（1）可证得△FDM∽△FCE，从而得出，进而求得结果；
（2）连接AE，AF，可证得△ABE≌△ADF，进而得出△AEF是等腰直角三角形，可证得△AFN∽△MEQ，进一步得出结论；
（3）作EG⊥AD于G，可证得△ABE∽△FCE，从而求得BE的长，进而求得，根据＝，进一步求得结果．
【解答】（1）解：∵四边形ABCD是正方形，
∴CD＝BC＝AB＝6，AD∥BC，
∴△FDM∽△FCE，
∴，
∵BE＝DF，
∴CE＝BC﹣BE＝6﹣BE，CF＝CD+DF＝6+BE，
∴，
∴BE＝2或BE＝3；
（2）证明：如图1，
连接AE，AF，
∵四边形ABCD是正方形，
∴∠BAD＝∠B＝∠ADC＝∠ADF＝90°，AB＝AD，∠CAD＝45°，
∵BE＝DF，
∴△ABE≌△ADF（SAS），
∴AE＝AF，∠BAE＝∠DAF，
∴∠BAE+∠DAE＝∠DAF+∠DAE，
∴∠EAF＝∠BAD＝90°，
∴△AEF是等腰直角三角形，
∴AE＝AF＝EF，∠AEF＝∠AFE＝45°，
∵∠AME＝∠AFE+∠FAD＝45°+∠FAD，
∠NAF＝∠CAD+∠FAD＝45°+∠FAD，
∴∠AME＝∠FAN，
∴△FAN∽△EEMA，
∴＝，
∴AE•AF＝FN•EM，
∴（EF）2＝FN•EM，
∴EF2＝2EM•FN；
（3）解：如图2，
连接BD，
则BD⊥AC，
当AN＝MN时，
∠AMN＝∠CAD＝45°，
此时∠ANNM＝90°，即：MN⊥AC，
∴BD∥MN，这种情形不存在，
当AM＝MN时，EF⊥AD，这种情形也不存在，
如图3，
当AM＝AN时，作EG⊥AD于G，
∴∠ANM＝∠AMN＝＝67.5°，
∵AD∥BC，
∴∠CEF＝∠AMN＝67.5°，
∵∠AEF＝45°，
∴∠AEB＝180°﹣45°﹣67.5°＝67.5°，
∴∠AEB＝∠CEF，
∵∠ABC＝∠ADF＝90°，
∴△ABE∽△FCE，
∴，
设BE＝CF＝a，
∴CE＝6﹣a，CF＝6+a，
∴，
∴a1＝6﹣6，a2＝﹣6（舍去），
∵∠AMN＝∠AME，∠MAN＝∠AEM＝45°，
∴△AMN∽△AMA，
∴，＝（）2，
∵AM＝AN，
∴AE＝EM，
∴GM＝AG＝BE，
∵（）2＝＝，
∴S△EAM＝＝＝36，
∴＝4×，
∴S△AMN＝108﹣144．
【点评】本题考查了正方形性质，等腰三角形的性质和分类，相似三角形的判定和性质等知识，解决问题的关键是作辅助线，构造全等三角形．
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2024/11/25 0:29:56；用户：15008208124；邮箱：15008208124；学号：60148633