
重庆市第八中学校2025届九年级上学期期中考试数学试卷(含答案)
展开
这是一份重庆市第八中学校2025届九年级上学期期中考试数学试卷(含答案),共30页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
一、单选题
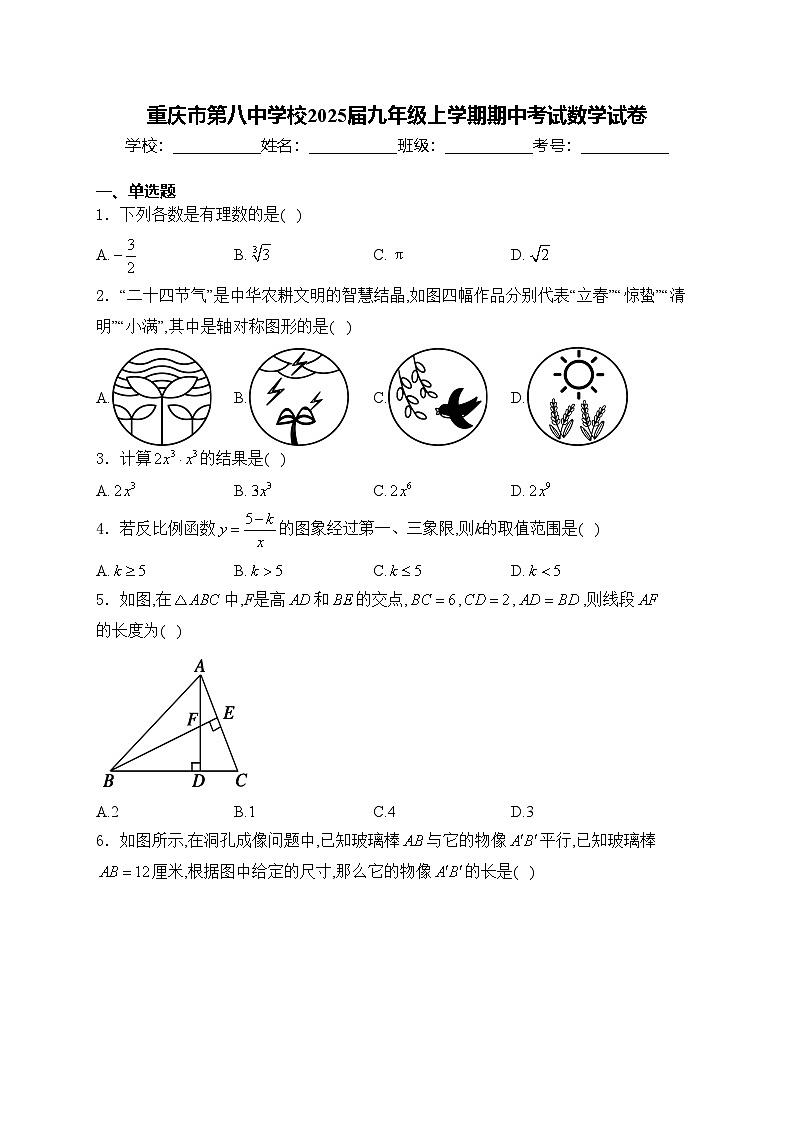
1.下列各数是有理数的是( )
A.B.C.D.
2.“二十四节气”是中华农耕文明的智慧结晶,如图四幅作品分别代表“立春”“惊蛰”“清明”“小满”,其中是轴对称图形的是( )
A.B.C.D.
3.计算的结果是( )
A.B.C.D.
4.若反比例函数的图象经过第一、三象限,则k的取值范围是( )
A.B.C.D.
5.如图,在中,F是高和的交点,,,,则线段的长度为( )
A.2B.1C.4D.3
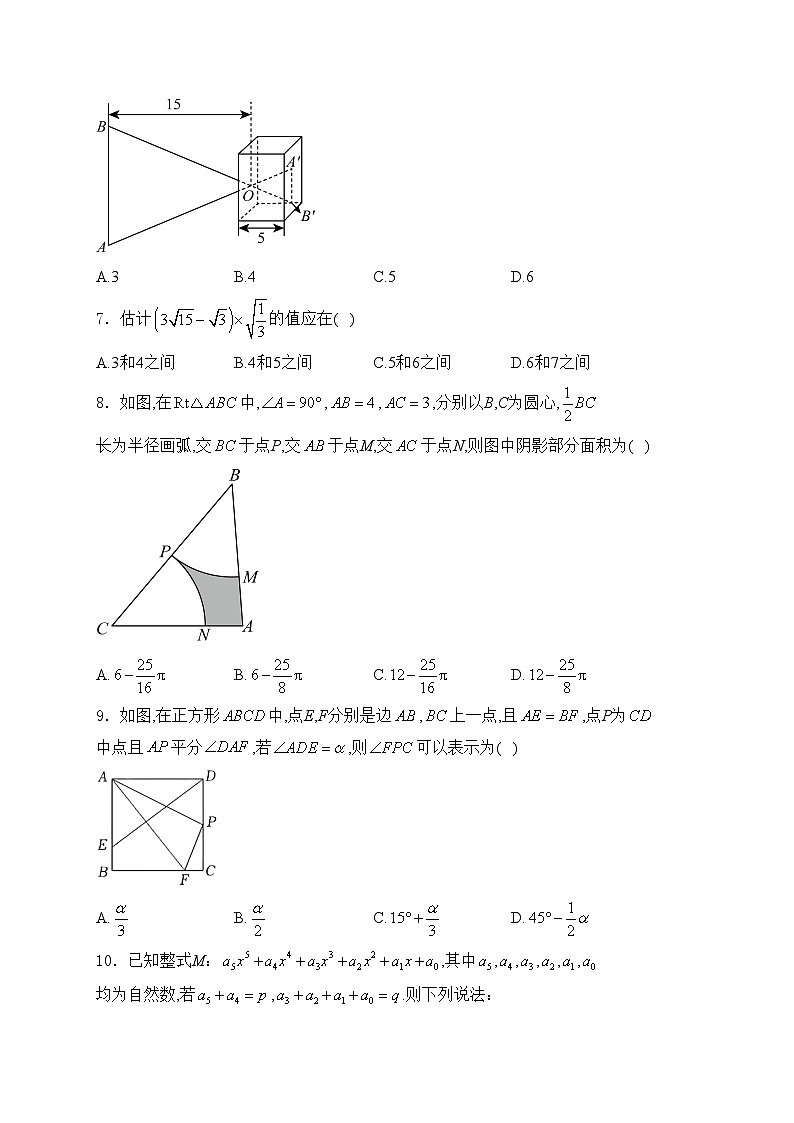
6.如图所示,在洞孔成像问题中,已知玻璃棒与它的物像平行,已知玻璃棒厘米,根据图中给定的尺寸,那么它的物像的长是( )
A.3B.4C.5D.6
7.估计的值应在( )
A.3和4之间B.4和5之间C.5和6之间D.6和7之间
8.如图,在中,,,,分别以B,C为圆心,长为半径画弧,交于点P,交于点M,交于点N,则图中阴影部分面积为( )
A.B.C.D.
9.如图,在正方形中,点E,F分别是边,上一点,且,点P为中点且平分,若,则可以表示为( )
A.B.C.D.
10.已知整式M:,其中,,,,,均为自然数,若,.则下列说法:
①若,,则所有可能的取值有4个;
②若p,q满足方程,且,则满足条件的不同整式有12个;
③若,当时,该方程存在5个实数解记为,,,,,若,且,则p存在最大值为25
其中,正确的个数是( )
A.3个B.2个C.1个D.0个
二、填空题
11.计算:______.
12.若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是______.
13.已知a为方程的一个根,则______.
14.有5个外观完全相同且密封不透明的试剂瓶,分别装有稀硫酸、稀盐酸、氯化钠、碳酸钠和氢氧化钠五种溶液,小星从这5个试剂瓶中任意抽取2个,则抽到的2个都是酸性溶液(稀硫酸溶液、稀盐酸溶液)的概率是______.
15.如图,是的弦,B为上一点,连接,,若,,则的半径长为______.
16.若关于x的一元一次不等式组有且仅有3个偶数解,且关于y的分式方程的解为非负整数,则所有满足条件的整数a的值之和是______.
17.如图,在平行四边形中,M、N分别是边、上动点.将四边形沿直线折叠,点D的对应点恰好落在边上,C的对应点为,连接、,其中交于点P.若,,,则的长度为______.
18.若一个四位数满足M的千位数字与百位数字的和与它们的差的积恰好是M的后两位数字组成的两位数,则称这个四位数M为“均衡数”,则最大的“均衡数”为______;将均衡数M的千位数字与十位数字对调,百位数字与个位数字对调得到的新数记为,记,,当、均为整数时,则满足条件的所有M的中位数为______.
三、解答题
19.计算:
(1);
(2).
20.小文非常喜效钻研数学,学了多边形的相关知识后,她知道了n边形的内角和等于,那么四边形的内角和是,于是她想探究:如果一个四边形(轴对称图形除外)的一组对角都为,那么另一组对角的角平分线有怎样的位置关系?请完成以下作图和填空:
如图,在四边形中,,平分.
(1)尺规作图:作的角平分线,交于点F(只保留作图痕迹).
(2)探究:与的位置关系.将下面的过程补充完整.
解析:∵且,
∴①
∵平分、平分,
∴,,
∴.
∵在中,,
∴②
∴③
通过推理论证,小红得到如下结论:如果一个四边形(轴对称图形除外)的一组对角都为,那么④
21.随着智能家居设备的流行,一家科技公司推出了两款最新的智能家居设备.用户体验团队对A,B两款智能家居设备的用户满意度进行了评分测验,并从中各随机抽取20份测验数据,对数据进行整理、描述和分析(评分分数用x表示,分为四个等级:不满意,比较满意,满意,非常满意),下面给出了部分信息:
抽取的对A款智能家居设备的评分中“满意”的数据:84,86,86,87,88,89;
抽取的对B款智能家居设备的评分数据:66,68,69,81,84,85,86,87,87,87,88,89,95,97,98,98,98,98,99,100.
抽取的对A,B两款智能家居设备的评分统计表
根据以上信息,解答下列问题:
(1)上述图表中________,________,________;
(2)根据以上数据,你认为哪款智能家居设备更受用户喜爱?请说明理由(写出一条理由即可);
(3)在此次测验中,有320人对A款智能家居设备进行评分、260人对B款智能家居设备进行评分,估计此次测验中对智能家居设备不满意的共有多少人?
22.市中心的一家时尚咖啡店推出了两款新颖的特色饮品,一款是“陨石拿铁”另一款是“摘星摩卡”.已知2杯“陨石拿铁”和5杯“摘星摩卡”总售价为240元;3杯“陨石拿铁”和4杯“摘星摩卡”总售价为234元.
(1)求“陨石拿铁”和“摘星摩卡”各自的单价;
(2)咖啡豆是制作咖啡饮品的主要原料之一,咖啡店老板发现今年第三季度平均每千克咖啡豆的价格比第二季度上涨了,第三季度花元买到的咖啡豆数量比第二季度花同样的钱买到的咖啡豆数量少了12千克,求第三季度咖啡豆的单价.
23.如图,四边形为矩形,,,点E为线段(不包含点A与点B)上一动点,点F为射线上一动点,且,设,.
(1)请直接写出与x之间的函数关系式及对应的x的取值范围;
(2)请在给定的平面直角坐标系中画出的函数图象,并写出该函数的一条性质;
(3)若函数的图象与的图象有两个交点,请直接写出b的取值范围.
24.舞龙俗称舞龙灯,源自古人对龙的崇拜,每逢佳节人们都会舞龙,以此方式来祈求平安和丰收,春节前夕在某广场举行了一次舞龙表演.如图,表演场地在点C处,已知小明家A在表演场地C南偏西方向上.小明有两条路线去看表演,路线①:从小明家A穿过一公园D,再沿到达表演场地C,其中点D在点A的东北方向上,点C在点D的北偏东方向上且距离点D米处;路线②:从小明家A出发沿正东方向到达十字路口B,再沿正北方向到达表演场地C.
(A、B、C、D在同一平面内,参考数据:,,,,,)
(1)求小明家A到公园D的距离;(结果保留根号)
(2)小明和爸爸一起去看表演,他们计划出门,爸爸选择路线①步行前往,步行的平均速度,小明选择路线②骑自行车前往,骑车的平均速度是,若表演正式开始的时间是,小明和爸爸能否在表演正式开始前到达表演场地C,请通过计算说明理由.(结果保留1位小数)
25.如图,在平面直角坐标系中,已知抛物线与x轴交于A,B两点,与y轴交于点C,其中,,连接,.
(1)求该抛物线的解析式;
(2)点P为直线下方抛物线上一点,过点P作交y轴于点D,求的最大值及此时点P的坐标;
(3)将该抛物线沿射线方向平移,经过点B时得到新抛物线,在新抛物线上有一点M,过点M作轴于点N.若以B,M,N三点为顶点的三角形与相似,写出所有符合条件的点M的坐标,并写出求解点M的坐标的其中一种情况的过程.
26.为等边三角形,点D为平面内一点且,连接.
(1)如图1,已知,,点E为中点,连接,求;
(2)如图2,点E为中点,连接,请用等式表示线段和的数量关系,并证明;
(3)如图3,在(1)问的条件下,点M、N分别是、上的动点,连接,,且,当取最小值时,请直接写出四边形的面积.
参考答案
1.答案:A
解析:A.是有理数,符合题意,
B.是无理数,不符合题意,
C.是无理数,不符合题意,
D.是无理数,不符合题意,
故选A.
2.答案:A
解析:选项B、C、D均不能找到这样的一条直线,使图形沿该直线对折后直线两旁的部分能够完全重合,所以不是轴对称图形,
选项A能找到这样的一条直线,使图形沿该直线对折后直线两旁的部分能够完全重合,所以是轴对称图形.
故选A.
3.答案:C
解析:.
故选:C.
4.答案:D
解析:∵反比例函数的图象经过第一、三象限,
∴,
解得:,
故选D.
5.答案:A
解析:∵,,
∴,
∴
∵和是三角形的高
∴
∴,
∴
在和中
∴
∴
∴
故选A
6.答案:B
解析:过点O作于点C,延长交于点,如图,
,
依题意得:,,
∵,,
∴,
∵,
∴,
∴,即,
∴厘米,
故选:B.
7.答案:C
解析:原式,
∵,
,
∴
∴的值在5和6之间,
故选C.
8.答案:A
解析:∵,,,
∴,,
∵以B,C为圆心,长为半径画弧,
∴扇形和扇形的半径相同,均为,
∴两个扇形的面积之和为,
∴阴影部分的面积为:;
故选A.
9.答案:D
解析:如图,过P作于点G,
平分,
,
,
是中点
四边形是正方形
,,
,
,
故选:D.
10.答案:B
解析:∵,,,,均为自然数,
∴最大为3.
∴可取3,2,1,0,所有可能的取值有4个.
说法①正确.
∵,
∴.
∴.
∵,
∴的最小取值.
∴只能表示为,且,.
∴,.
∴,可能的组合为2,0或者0,2或者1,1,共三种组合;,,,可能的组合为6,2,1,0或者5,3,1,0或者4,3,2,0,共三种组合.
∴满足条件的不同整式有:(个).
说法②错误.
由题意得.
∵,
∴.
∴.
∴.
∴.
∴的对称轴为.
∵,为自然数,n不为,
∴n为正整数.
∵,当时,随着n增大,p逐渐减小,
∴当时,p可以取得最大值.
说法③正确.
综上所述,说法正确的为①③.
故选:B.
11.答案:
解析:,
故答案为:
12.答案:8
解析:设边数为n,由题意得,
,
解得.
所以这个多边形的边数是8.
故答案为:8.
13.答案:
解析:∵a为方程的一个根,
∴,
∴,
∴
.
故答案为:.
14.答案:
解析:氯化钠、碳酸钠、氢氧化钠、稀硫酸、稀盐酸5个试剂瓶分别用表示,列表如下:
由表可知共有20种可能的结果,其中抽到2个都是酸性溶液的情况有2种,
则抽到的2个都是酸性溶液的概率为.
故答案为:.
15.答案:
解析:∵,
∴,
∵,,
∴,
∴
∵,
∴,
∴,
即的半径长为.
故答案为:.
16.答案:
解析:解不等式
得
解得
一元一次不等式组有且仅有3个偶数解,
解得,
解
解得,
关于y的分式方程的解为非负整数,
为非负整数,且
则
又
解得,,
整数a的值之和为:.
故答案为:.
17.答案:
解析:连接,在上截取,连接,
由折叠性质可知,垂直平分,
∴,,,,
∴,
∴,
∵四边形是平行四边形,
∴,,,,
∵,
∴是等边三角形,
∴,,
∴,
∵,
∴,
∵,,
∴,
∴,,
∵,
∴,
∴,
过作,交延长线于点F,
∴,
∴,
∴,
∴,
在中,由勾股定理得:,
设,则,,
在中,由勾股定理得:,
∴,解得,
∴,
∴在中,由勾股定理得:,
∴,
∴在中,由勾股定理得:,
故答案为:.
18.答案:9817;6327
解析:千位数字最大为9,再根据“均衡数”的定义可知百位数字最大为8,则,
所以最大的“均衡数”是9817;
故答案为:9817;
∵是整数,
∴a是b的倍数,且,
当,时,,,则,不是整数,舍;
当,时,,,则,不是整数,舍;
当,时,,,则;
当,时,,,则,不是整数,舍;
当,时,,,则,不是整数,舍;
当,时,,,则,不是整数,舍;
当,时,,,则,是整数;
当,时,,,则,不是整数,舍;
当,时,,,则,不是整数,舍;
当,时,,,则,不是整数,舍;
当,时,,,则,是整数;
当,时,,,则,不是整数,舍.
符合题意的有8448,6327,4212,
所以中位数是6327.
故答案为:6327.
19.答案:(1)
(2)
解析:(1)
.
(2)
.
20.答案:(1)见解析
(2);;;另一组对角的角平分线互相平行
解析:(1)如图,为的角平分线,
(2)∵且,
∴,
∵平分、平分,
∴,,
∴.
∵在中,,,
∴,
∴
通过推理论证,小红得到如下结论:如果一个四边形(轴对称图形除外)的一组对角都为,那么另一组对角的角平分线互相平行.
21.答案:(1)15;88.5;98
(2)A款智能家居设备更受用户喜爱,理由见解析
(3)71人
解析:(1)由题意得:,
即,
款的评分非常满意有(个),“满意”的数据为84、86、86、87、88、89,
把A款的评分数据从小到大排列,排在中间的两个数是88、89,
中位数,
在B款的评分数据中,98出现的次数最多,
众数;
故答案为:15,88.5,98;
(2)A款智能家居设备更受用户喜爱,理由如下:
两款的评分数据的平均数相同都是88,但款评分数据的中位数为88.5比款的中位数87.5高,
∴A款智能家居设备更受用户喜爱(答案不唯一);
(3)(人),
答:此次测验中对智能家居设备不满意的共有71人.
22.答案:(1)“陨石拿铁”的单价为30元,“摘星摩卡”的单价为36元
(2)第三季度咖啡豆的单价为元/千克
解析:(1)(1)设“陨石拿铁”的单价为x元,“摘星摩卡”的单价为y元,
根据题意得:,
解得:.
答:“陨石拿铁”的单价为30元,“摘星摩卡”的单价为36元.
(2)设第二季度咖啡豆的单价为m元/千克,则第三季度咖啡豆的单价为元/千克,
根据题意得:,
解得:,
经检验,是所列方程的解,且符合题意,
∴.
答:第三季度咖啡豆的单价为元/千克.
23.答案:(1)
(2)画图见解析,当时,y随x的增大而增大(答案不唯一)
(3)
解析:(1)∵四边形为矩形,
∴,,
∴,
∵,
∴,
∴,
∴,
∴,
当点F与C点重合时,,则:,
当点F在线段上时,此时:,,
∴,
∴;
当点F在线段的延长线上时,此时:,,
∴,
∴;
综上:;
(2)列表如下:
描点,连线,画出函数图象如图:
由图象可知:当时,y随x的增大而增大;
(3)由图象可知,当过点时,此时,,
此时直线与的图象有1个交点,
将直线向上平移,直至过点,此时直线的解析式为:,即,直线与的图象有1个交点,
∴当时,直线与的图象有2个交点.
24.答案:(1)米
(2)爸爸不能在表演正式开始前到达表演场地C,理由见解析;小明能在表演正式开始前到达表演场地C,理由见解析
解析:(1)过点D作于点F,作于点E,则,
∵,
∴四边形是矩形,
∴,
在中,米,
∴(米),(米),
∴(米),
设米,
在中,,
∴米,
∴米,
在中,,
∴,
∴,
解得,
即小明家A到公园D的距离为米;
(2)爸爸不能在表演正式开始前到达表演场地C,理由如下:
由(1)可知,米,
∴,
即爸爸的时间为,
∵,
∴爸爸不能在表演正式开始前到达表演场地C;
小明能在表演正式开始前到达表演场地C,理由如下:
由(1)可知,
米,
∴,
即小明的时间为,
∵,
∴小明能在表演正式开始前到达表演场地C;
25.答案:(1),详见解析
(2)最大值为,此时P点坐标为:,详见解析
(3)点M的坐标为:,,,详见解析
解析:(1)∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
将A、B、C三点代入得,
∴,解得,
∴抛物线的解析式为;
(2)如图,过P点轴交y轴于点F,设,
∵,
∴,
∴,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∴当时,有最大值为,
∴当时,,
∴最大值为,P点坐标为:;
(3)∵将该抛物线沿射线方向平移,,
∴设抛物线沿x轴正半轴方向平移个单位,则沿y轴正方向平移n个单位,
∵,
∴平移后的函数解析式为,
∵新抛物线经过点B,
∴,
解得(舍)或,
∴平移后的函数解析式为,
∵在新抛物线上有一点M,过点M作轴于点N,设M的横坐标为t,
∴,,
如图,
当时,,
∴,
∴,
解方程得:,,,,
当时,,
∴,
∴,
∴,,
∴将,,,,分别代入得到点M的纵坐标为:,0,0,,,
∵点,在x轴上,
∴与点N重合,构不成三角形,,不符合题意,舍去,
∴点M的坐标为:,,.
26.答案:(1)
(2),理由见解析
(3)
解析:(1)∵为等边三角形,
∴,
∵点E为中点,
∴,,
∵,,
∴,,
∴,
∴,
由勾股定理得:,
∴,
同理得:,
∵,,
∴,
∴;
(2),理由如下:
如图,延长至Q,使得,连接、,延长至K,使得,连接,
∵点E为中点,
∴,
在和中,
,
∴,
∴,,
∴,
∴,
∴,
∵,,
∴是等边三角形,
∴,,
∴,
∴,
∴,
在和中,
,
∴,
∴,,
∴,,
∴,
在和中,
,
∴,
∴;
(3)∵,
∴,
如图,作,交于点T,
∴,
∴,
∴四边形是平行四边形,
∴,
∴,
作C关于对称点,连接、,
∴,是等边三角形,
当T、N、共线时,且时,取最小值,
∴T为中点,N为中点,
∴,
∴,
∵,
∴,
∴,,,
∴,
∴.
设备
平均数
中位数
众数
“非常满意”所占百分比
A
88
b
96
45%
B
88
87.5
c
40%
1
2
3
4
5
2
0
2
4
6
相关试卷
这是一份重庆市第八中学校2024届九年级中考一模数学试卷(含答案),共30页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
这是一份重庆市第八中学校2024届九年级中考一模数学试卷(含解析),共31页。试卷主要包含了选择题,解答题等内容,欢迎下载使用。
这是一份重庆市第八中学校2024届九年级中考一模数学试卷(含解析),共31页。试卷主要包含了选择题,解答题等内容,欢迎下载使用。









