重庆市凤鸣山中学2025届九年级上学期12月月考数学试卷(含答案)

这是一份重庆市凤鸣山中学2025届九年级上学期12月月考数学试卷(含答案)，共25页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

一、单选题
1．的倒数是( )
A.B.C.2025D.
2．引发秋季传染病的某种病毒的直径是,将用科学记数法表示为( )
A.B.C.D.
3．下列图形中,是轴对称图形的是( )
A.B.
C.D.
4．反比例函数的图象经过点,则k的值为( )
A.B.C.8D.
5．估计的运算结果应在哪两个数之间( )
A.5和6B.6和7C.7和8D.8和9
6．下列命题正确的是( )
A.顺次连接矩形四边中点构成的四边形是菱形
B.同位角相等
C.有两边及一角对应相等的两个三角形全等
D.三角形的外心到三角形三条边的距离相等
7．如图,四边形与四边形位似,位似中心是O,若,且四边形的周长为3,则四边形的周长为( )
A.6B.9C.12D.27
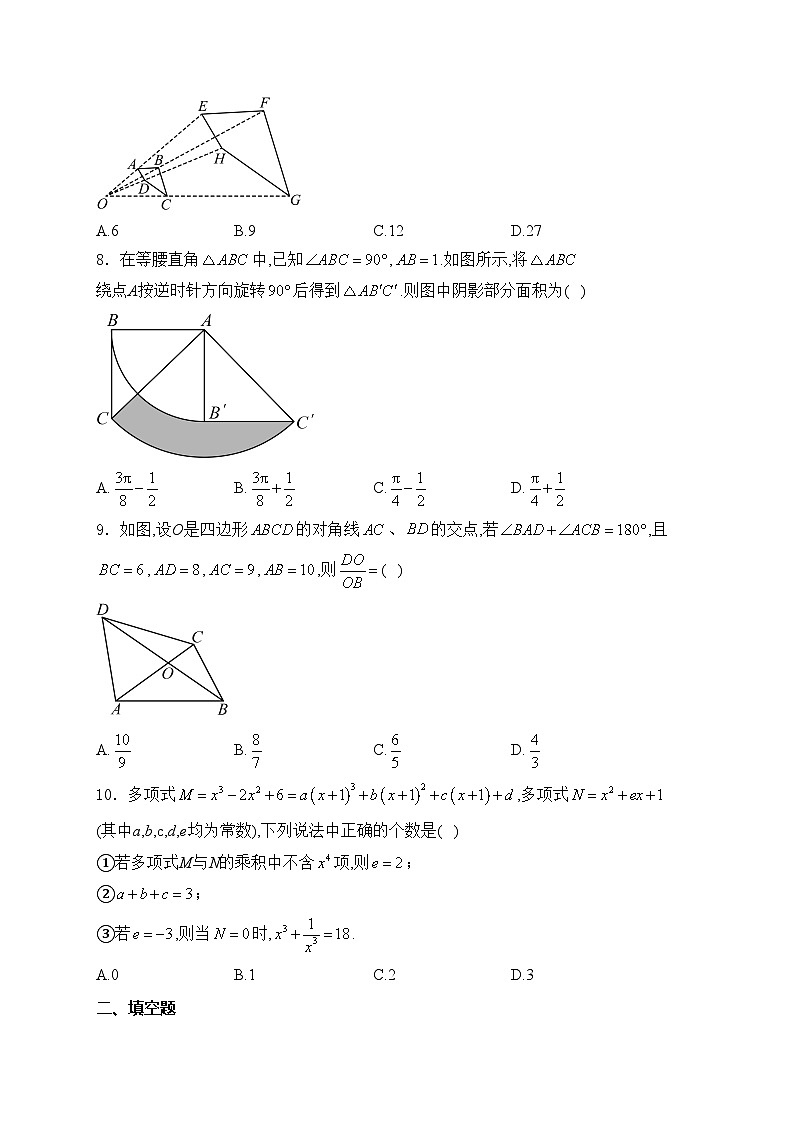
8．在等腰直角中,已知,.如图所示,将绕点A按逆时针方向旋转后得到.则图中阴影部分面积为( )
A.B.C.D.
9．如图,设O是四边形的对角线、的交点,若,且,,,,则( )
A.B.C.D.
10．多项式,多项式(其中a,b,c,d,e均为常数),下列说法中正确的个数是( )
①若多项式M与N的乘积中不含项,则；
②；
③若,则当时,.
A.0B.1C.2D.3
二、填空题
11．计算：______.
12．现将背面完全相同,正面分别标有数0,1,2,5的4张卡片洗匀后,背面朝上,从中任取两张,则两张卡片的数字均为奇数的概率为______.
13．如果一个多边形的每一个内角都等于,那么这个多边形是______边形.
14．一条直线上有n个点,共形成了28条线段,则n的值为______.
15．如图,矩形中,E为边上一点,,.若沿翻折后得到,点F恰好在线段上,则的长为______.
16．若关于x的不等式组有解,关于y的分式方程有非负数解,则符合条件的所有整数a的和为______.
17．如图,在中,,E是弧的中点,若,,则______.
18．一个四位自然数M的各个数位上的数字互不相等且都不等于0,如果前两位数字所组成的两位数与后两位数字所组成的两位数的和等于100,那么就称这个数为“奋进数”.把“奋进数”M的前两位数字和后两位数字整体交换得到新的四位数.并且规定：.例如：一个四位数3268,因为,所以3268是“奋进数”,且.如果四位自然数(,且a,b,c,d为整数)是一个“奋进数”,则______(用含a,b的代数式表示),另外规定等于M的前两位数字之和.如果S是一个“奋进数”,为偶数,且(k为整数),则满足条件的S的最小值是______.
三、解答题
19．计算：
(1)；
(2).
20．为迎接明年4月份的体育考试,九年级开展了本学期周末锻炼次数调查,便于开展后期针对性训练.现从本年级男生、女生中各抽取20名学生锻炼次数(记为次)进行分析,将锻炼次数分为以下4组,A组：；B组：；C组：；D组：；现将数据收集、整理、分析如下.
收集数据：
男生：5,6,8,9,7,1,10,3,4,8,5,0,7,2,7,6,8,4,8,11.
女生20名学生中的次数分别是：9,7,8,9,9,8,9,8,
整理数据：
分析数据：
根据以上信息,解答下列问题：
(1)上述表中的________,________,________,________；
(2)通过以上数据分析,你认为男生还是女生锻炼的情况更好,请说明理由.(一条理由即可)
(3)若锻炼在7次及以上为优秀,九年级男生400名,女生360名,请估计九年级锻炼优秀的学生总人数是多少？
21．在学习角平分线判定的过程中,小凤遇到一个问题：在四边形中,,,交于点E.求证：平分.他的思路,首先过点D作的垂线,利用三角形全等得两垂线段相等,由角平分线的判定,使问题得到解决.请根据小凤的思路完成下面的作图和填空.
证明：用直尺和圆规,过点D作的垂线,垂足为F.(保留作图痕迹)
∵,,
∴①,
∵,,
∴②,
又∵③,
∴④,
∴⑤,
∵,,
∴平分.
22．如图所示,已知是水平面,、、是斜坡,A、B、C、D在同一个平面内.在坡顶A处测得B点的俯角为,米,在坡顶A处测得D点的俯角为,米,的坡比.
(1)求坡顶A到水平面的距离；
(2)求斜坡的长度.(结果精确到1米,参考数据：,)
23．今年春节假期国内又将迎来旅游高峰,滑雪游成为热门主题,许多市民选择前往沙坪坝区的融创茂雪世界进行滑雪体验.
(1)该雪世界提供成人票和儿童票两种选择,其中一张成人票比一张儿童票贵元,购买2张成人票和1张儿童票的总费用为元.求成人票价和儿童票价分别是多少元？
(2)某滑雪装备店销售成人及儿童所需的雪具,其中成人雪具的价格比儿童雪具贵,有顾客发现,用元购买成人雪具的数量比用同样金额购买儿童雪具的数量少套,求成人雪具的单价.
24．如图,在中,,,点P为上一点,过点P作交于点Q.设的长度为x,点P,Q的距离为,的周长与的周长之比为.
(1)请直接写出,分别关于x的函数表达式,并注明自变量x的取值范围；
(2)在给定的平面直角坐标系中画出函数,的图象；请分别写出函数,的一条性质；
(3)结合函数图象,直接写出时x的取值范围.(近似值保留一位小数,误差不超过)
25．如图1,在平面直角坐标系中,抛物线与x轴交于A,B两点,与y轴交于点C,已知,,.
(1)求抛物线的解析式；
(2)在线段上有一动点D,过点D作交抛物线于点E,过点E作y轴的平行线交于点F.求的最大值,以及此时点E的坐标；
(3)如图2,将该抛物线沿y轴向下平移2个单位长度得到新抛物线,若点P为新抛物线上一点,且满足,请直接写出所有符合条件的点的坐标.
26．在中,,D是上一点.
(1)如图,E是的中点,,,,求线段的长度；
(2)如图,,点F在线段上,将线段绕点C顺时针旋转得到线段,连接,交于点H,当时,猜想并证明与的关系.
参考答案
1．答案：D
解析：根据倒数的定义可得：
的倒数是,
故选：D.
2．答案：B
解析：,
故选：B.
3．答案：C
解析：A、不是轴对称图形,故选项不符合题意；
B、不是轴对称图形,故选项不符合题意；
C、是轴对称图形,故选项符合题意；
D、不是轴对称图形,故选项不符合题意；
故选：C.
4．答案：D
解析：∵反比例函数的图象经过点,
∴,
∴,
故答案为：D.
5．答案：C
解析：∵,,
∴,
即：的运算结果应在7和8之间,
故选：C.
6．答案：A
解析：A、顺次连接矩形四边中点构成的四边形是菱形,正确,故选项符合题意；
B、两直线平行,同位角相等,故选项不符合题意；
C、有两边及夹角对应相等的两个三角形全等,故选项不符合题意；
D、三角形的外心到三角形的三顶点的距离相等,故选项不符合题意；
故选：A.
7．答案：B
解析：∵,
∴,
∵四边形与四边形位似,位似中心是O,
∴四边形与四边形的相似比为,
∴四边形的周长四边形的周长,
∵四边形的周长为3,
∴四边形的周长为,
故选：B.
8．答案：A
解析：∵等腰直角中,,,
∴,,
由旋转可得,,,
∴,
∴,
故选：A.
9．答案：C
解析：过B作交延长线于点E,如图：
,
,
,,
,
,
故选：C.
10．答案：D
解析：
,
多项式M与N的乘积中不含项,
,
解得,说法①正确；
当时,,即
当时,,
则,说法②正确；
若,则当时,,
当时,,
∴,
等式两边同时除以x得,,即,
∴,即,
∵,
∴,说法③正确；
故选：D.
11．答案：
解析：
,
故答案为：.
12．答案：
解析：画树状图如下：
由树状图可得,共有种等结果,其中两张卡片的数字均为奇数的有2种结果,
∴两张卡片的数字均为奇数的概率为,
故答案为：.
13．答案：8/八
解析：多边形的每一个内角都等于,
多边形的每一个外角都等于,
边数.
故答案是：8.
14．答案：8
解析：∵一条直线上有n个点,共形成了28条线段,
∴,
整理得：,
∴,
解得：,(不合题意,舍去),
故答案为：8.
15．答案：
解析：∵四边形是矩形,
∴,,,
由折叠得,,,,
∴,,
∴,
∵,,
∴,
∴,
∴,
设,则,
在中,,
∴,
解得,
∴,
故答案为：.
16．答案：
解析：,
解不等式得：,
∵关于x的不等式组有解,
∴,解得,
由,解得：,
∵关于y的分式方程有非负数解,
∴且,
解得：且,
∴a的取值范围为且,
∴所有整数a为,,0,1,
∴符合条件的所有整数a的和为,
故答案为：.
17．答案：
解析：∵,
∴,
∵,,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∵E是弧的中点,
∴,
∴,
∴,
∴,
故答案为：.
18．答案：；5941
解析：∵,是奋进数,
∴,,,
∴,
,
设,且为偶数,
∴a,b同奇同偶,,
∴
,
∵,
∴,
∴,
∴,
∵,
∵a,b同奇同偶,且S最小,
∴a必须最小；
当时,,舍去,
当时,,
∴,则,此时,不符合题意,舍去,
当时,则,
当时,,此时,不符合题意,舍去,
当时,,此时,不符合题意,舍去,
当时,则,
当时,,,不符合题意,舍去,
当时,,则,不符合题意,舍去,
当时,则,
此时,都不符合题意；
当时,则,此时符合题意,
∴,
∴S的最小值为；
故答案为：；
19．答案：(1)
(2)
解析：(1)
；
(2)
.
20．答案：(1)4,8,8,
(2)女生锻炼的较好,理由：女生的中位数、众数都比男生的高
(3)九年级锻炼优秀的学生总人数约为人
解析：(1)抽取的名男生中,锻炼次数在中的有4人,
∴,
锻炼次数在中的有8人,
∴,
抽取的名男生中,锻炼次数出现次数最多的是8,共出现4次,
∴,
将女生的锻炼次数从小到大排列,处在中间位置的两个数为和,
∴,
故答案为：4,8,8,；
(2)由题意可知,女生锻炼的较好,理由：女生的中位数、众数都比男生的高；
(3)由题意可得：
(人),
∴九年级锻炼优秀的学生总人数约为人.
21．答案：画图见解析；,,,,
解析：证明：过点D作的垂线,垂足为F,
∵,,
∴,
∵,,
∴,
又∵,
∴,
∴,
∵,,
∴平分,
故答案为：,,,,.
22．答案：(1)米
(2)米
解析：(1)如下图所示,过点A作,
坡顶A处测得B点的俯角为,
,
,
,
解得：米,
坡顶A到水平面的距离为米；
(2)如下图所示,过点D作,,
四边形是矩形,
在坡顶A处测得D点的俯角为,
,
,
,
米,
在中米,
米,
,
的坡比,
设,则,
,
米,
斜坡的长度大约是米.
23．答案：(1)一张成人票的票价为元,一张儿童票的票价为元
(2)元
解析：(1)设一张儿童票的票价为x元,则一张成人票的票价为元,
由题意得,,
解得,
∴,
答：一张成人票的票价为元,一张儿童票的票价为元；
(2)设儿童雪具的价格为y元,则成人雪具的价格为元,
由题意得,,
解得,
经检验,是分式方程的解,符合题意,
∴,
答：成人雪具的价格为元.
24．答案：(1),
(2)画图见解析,性质：随x的增大而增大,随x的增大而减小(答案不唯一)
(3)
解析：(1)∵,
∴,
∴,
∴,,
∴,；
(2)画函数图象如下：
由函数图象可知,随x的增大而增大,随x的增大而减小；
(3)由函数图象可得,时x的取值范围为.
25．答案：(1)
(2)的最大值为3,
(3)或
解析：(1)∵,
∴,
∵,,
∴,
即,
∴,
∴,
∴,,
把、、代入得,
,
解得,
∴抛物线的解析式为；
(2)如图,延长交x轴于点G,
∵,,
∴,
∵,
∴,
∵,
∴,
∴为等腰直角三角形,
∴,
∴,
设直线的解析式为,把、代入得,
,
解得,
∴直线的解析式为,
设,则,
∴,
∴,
∵,
∴当时,的值最大,最大值为3,此时；
(3)∵,
将该抛物线沿y轴向下平移2个单位长度得到新抛物线,则,
当轴时,如图,有,此时点P的纵坐标为,
把代入得,,
解得,舍去,
∴；
作线段的垂直平分线,交x轴于点D,连接交抛物线于点P,可知,
∴,
设,
∵,
∴,
解得,
∴,
设直线的解析式为,把、代入得,
,
解得,
∴直线的解析式为,
由,解得舍去,,
∴；
综上,点P的坐标为或.
26．答案：(1)5
(2),证明见解析
解析：(1)如图,过点E作交于点G,则,
∵,,
∴,
∴,
∵,
∴,
解得,
∴,
∵E是中点,,
∴,,
∴是等腰三角形,
∴,
∴,
∵,
∴,
∴；
(2).
证明：如图,延长,在延长线上截取,取的中点Q,连接、,
∵线段绕点C顺时针旋转得到线段,
∴,,
∵,
∴,
∵,,
∴,
∴,
∴,,
设,则,
∵点C、Q分别为、的中点,
∴是的中位线,
∴,,
∴,
∵,,
∴,
∴,
∵,
∴,
即.
容量等级
男生
a
6
b
2
女生
4
5
8
3
平均数
众数
中位数
男生
c
女生
9
d