

2023-2024学年山东省青岛市崂山区八年级(上)期中数学试卷(解析版)
展开这是一份2023-2024学年山东省青岛市崂山区八年级(上)期中数学试卷(解析版),共17页。试卷主要包含了选择题,填空题,作图题,解答题等内容,欢迎下载使用。
一、选择题(本题共24分,共8小题,每小题3分)
1. 下列六个实数:0,,,,其中无理数的个数是( )
A. 2 个B. 3 个C. 4 个D. 5 个
【答案】B
【解析】∵,,,
∴,,是无理数,
故选B.
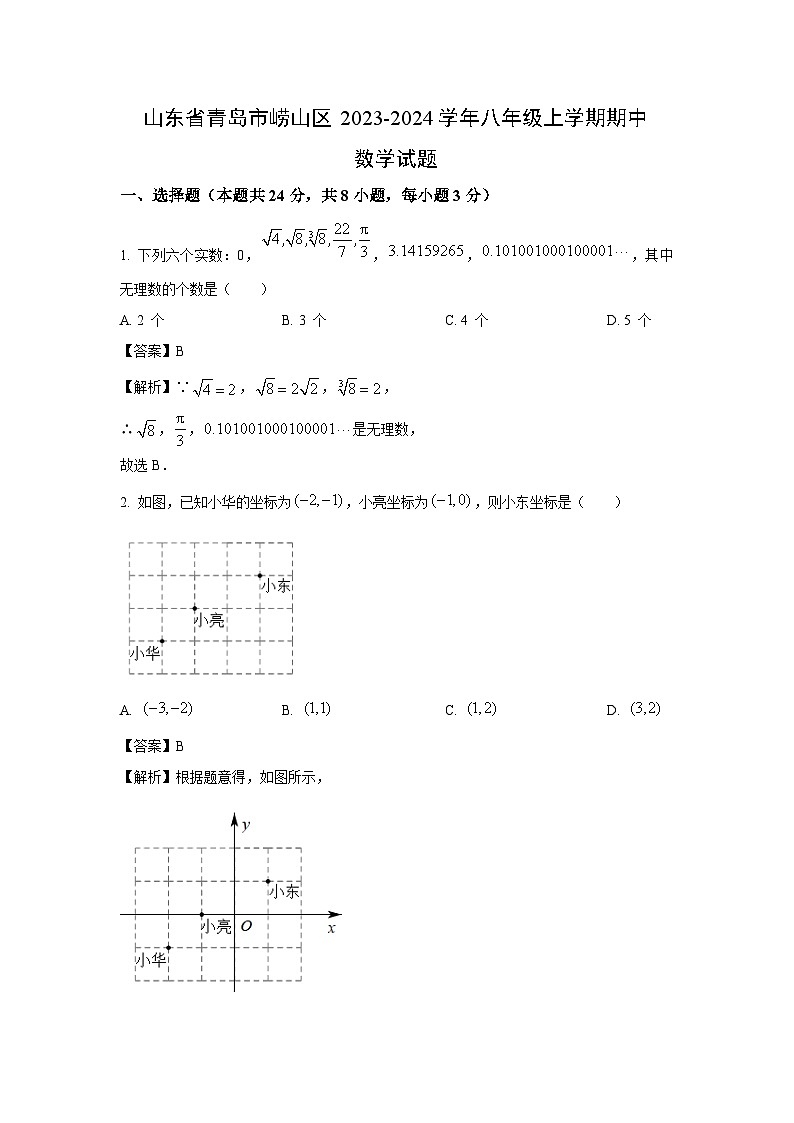
2. 如图,已知小华的坐标为,小亮坐标为,则小东坐标是( )
A. B. C. D.
【答案】B
【解析】根据题意得,如图所示,
∴小东的坐标是,
故选:.
3. 下列计算正确的是( )
A. B.
C. D.
【答案】D
【解析】A、,故原选项计算错误,不符合题意;
B、,故原选项计算错误,不符合题意;
C、,故原选项计算错误,不符合题意;
D、,故原选项计算正确,符合题意;
故选:D.
4. 若,,则函数的图象大致是( )
A. B. C. D.
【答案】A
【解析】由一次函数图象与系数的关系可得,
当k>0,b>0时,函数y=kx+b的图象经过一、二、三象限.
故选:A.
5. 若△ABC中、、的对边分别是a,b,c,下列条件不能说明△ABC是直角三角形的是( )
A. B.
C. D.
【答案】D
【解析】A.,
,
,
所以△ABC是直角三角形,故本选项不符合题意;
B.,
,
∴△ABC是直角三角形,故本选项不符合题意;
C.,
,
,
,
,
∴△ABC是直角三角形,故本选项不符合题意;
D.,,
最大角,
∴△ABC不是直角三角形,故本选项符合题意;
故选:D.
6. 如图,长方形的边长为2,边长为1,在数轴上,以原点O为圆心,对角线的长为半径画弧,交正半轴于一点,则这个点表示的实数是( )
A. B. C. D. 2.5
【答案】C
【解析】,,
,
以原点O为圆心,对角线的长为半径画弧,交正半轴于一点,则这个点表示的实数是,
故选:C.
7. 如图,在四边形中,,分别以四边形的四条边为边向外作四个正方形,若,,,则( )
A. 76B. 54C. 62D. 81
【答案】C
【解析】连接,
由题意得:,,,,
∵,
∴,
∴,
∴.
故选:C
8. 如图,动点M按图中箭头所示方向运动,第1次从原点运动到点,第2次运动到点,第3次运动到点,…,按这样的规律运动,则第2023次运动到点( )
A. B. C. D.
【答案】D
【解析】∵第1次从原点运动到点,第2次运动到点,第3次运动到点,第4次从原点运动到点,第5次运动到点,
∴动点的横坐标为,纵坐标按照四个为一组进行循环,
∵,
∴第2023次运动到点,即:;
故选D.
二、填空题(本题共24分,共8小题,每小题3分)
9. 的算术平方根是________.
【答案】2
【解析】∵,4的算术平方根是2,
∴的算术平方根是2.
故答案为:2.
10. 已知点、在直线上,则与大小关系是______
【答案】
【解析】,
,
随的增大而减小,
,
,
故答案为:.
11. 估计与最接近的整数是_____________.
【答案】6
【解析】∵
∴
∵
∴与最接近的整数是6.
故答案为:6.
12. 一个正数a的两个平方根分别是和,则_________.
【答案】
【解析】根据题意得,
解得:,
故答案为:.
13. 如图已知长方形ABCD中AB=8cm,BC=10cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,则CE的长为___________.
【答案】3cm
【解析】∵四边形ABCD是矩形,
∴AD=BC=10cm,CD=AB=8cm,
根据题意得:Rt△ADE≌Rt△AFE,
∴∠AFE=90°,AF=10cm,EF=DE,
设CE=xcm,则DE=EF=CD−CE=(8−x)cm,
在Rt△ABF中由勾股定理得:AB2+BF2=AF2,
即82+BF2=102,
∴BF=6cm,
∴CF=BC−BF=10−6=4(cm),
在Rt△ECF中,由勾股定理可得:EF2=CE2+CF2,
即(8−x)2=x2+42,
∴64−16x+x2=x2+16,
∴x=3(cm),
即CE=3cm.
故答案为3cm.
14. 一次函数的图像如图所示,则方程的解是___________.
【答案】
【解析】根据题意得,当时,一次函数图像与轴交点是,
∴方程的解是,
故答案是:.
15. 有一个数值转换器,原理如图,当输入的时,输出的等于________.
【答案】
【解析】第1次计算得,=4,而4是有理数,
因此第2次计算得,=2,而2是有理数,
因此第3次计算得,,是无理数,则输出.
故答案为:.
16. 如图,长方形中,,,E为边上的动点,F为的中点,连接,,则的最小值为______.
【答案】
【解析】作关于对称点,连接,,过作于点,则,,,,
,
,
当、、三点在同一直线上时,的值最小,
的最小值为:.
故答案为:.
三、作图题(6分)
17. 如图在平面直角坐标系中,A(3,4),B(1,2),C(5,1).
(1)作出△ABC关于y轴的对称图形△A1B1C1,并标出点A1,B1,C1.
(2)写出下列点坐标:A1( ),B1( ),C1( ).
(3)填空:△ABC的面积为: .
解:(1)如图,△A1B1C1为所作;
(2)由图可知:A1(﹣3,4),B1(﹣1,2),C1(﹣5,1);
故答案为:﹣3,4;﹣1,2;﹣5,1;
(3)△ABC的面积=4×3﹣×1×4﹣×2×3﹣×2×2=5.
故答案为:5.
四、解答题(本题满分66分,共有8小题)
18. 计算;
(1);
(2);
(3);
(4)
解:(1)
.
(2)
.
(3)
.
(4)
.
19. 已知的立方根是,2是的一个平方根,求的值.
解:∵的立方根是,2是的一个平方根,
∴,,
∴,,
∴.
20. 大泽山向外地运送一批葡萄,公路运输每千克需运费0.25元,运完这批葡萄还需其他费用800元;铁路运输每千克需运费0.6元.
(1)若运输的这批葡萄为千克,选择公路运输,所需费用为元;选择铁路运输,所需费用为元.请分别写出,与之间的关系式.
(2)若支出运费1500元,则选用哪种运输方式运输的葡萄多?
解:(1)公路运输每千克需运费0.25元,运完这批葡萄还需其他费用800元;铁路运输每千克需运费0.6元,
,
(2)令,解得:,
令,解得:,
,
公路运输的葡萄多.
21. 学校计划种植一块草坪,形状为如图所示的四边形,其中,,,,.若每种植1平方米草坪成本为元,求学校种植该草坪的成本为多少.
解:连接,
∵,
∴直角△ABC中,由勾股定理得,
即,
∴,
又∵,,
∴中,,
∴是直角三角形,
即,
∴,
∴(元),
答:学校种植该草坪的成本为元.
22. 如图,平面直角坐标系中,过点的直线垂直于轴,为直线上一点.若点从点出发,以的速度沿直线向左移动;点从原点同时出发,以的速度沿轴向右移动,
(1)多久后线段平行于轴?
(2)若点,且,求点的坐标.
解:(1)设点后线段平行于轴,
由题意得:,,,
,
轴,
,即,
解得:,
3秒后线段平行于轴;
(2)设点的坐标为,
,,
,,
,
,
解得:或,
点从原点同时出发,以的速度沿轴向右移动,
,
.
23. 共享电动车是一种新理念下的交通工具,主要面向的出行市场,现有两种品牌的共享电动车,给出的图象反映了收费(元)与骑行时间之间的对应关系,其中品牌收费方式对应,品牌的收费方式对应,且超过十分钟时,对应的函数关系式是,请根据相关信息,解答下列问题:
(1)求出图中函数,的图象交点的坐标;
(2)求关于的函数解析式;
(3)①如果小明每天早上需要骑行品牌或品牌的共享电动车去工厂上班,已知两种品牌共享电动车的平均行驶速度均为,小明家到工厂的距离为,那么小明选择___________品牌共享电动车更省钱.(填“”或“”)
②当为何值时,两种品牌共享电动车收费相差元?
解:(1)∵函数,的图象交点,且点的纵坐标为,品牌的收费方式对应,且超过十分钟时,对应的函数关系式是,
∴,解得,,
∴点的坐标为.
(2)函数经过点,,
∴设,
∴,解得,,
∴,
∴关于的函数解析式为.
(3)①,平均行驶速度均为,
∴行驶时间为,即,
∴骑行品牌的费用(元);
骑行品牌共享电动车,且,
∴费用(元);
∵,
∴小明选择骑行品牌共享电动车,
故答案为:;
②第一种情况,,
∴,解得,;
第二种情况,,
∴,解得,;
∴当为或时,两种品牌共享电动车收费相差元.
24. 小明在解决问题:已知a=,求2a2﹣8a+1的值,他是这样分析与解答的:
∵ a= ∴.
∴(a﹣2)2=3,即a2﹣4a+4=3.
∴ a2﹣4a=﹣1,
∴ 2a2﹣8a+1=2(a2﹣4a)+1=2×(﹣1)+1=﹣1.
请你根据小明的分析过程,解决如下问题:
(1)填空: , ;
(2)计算:;
(3)若a,求2a2﹣12a﹣5的值.
解:(1),
;
故答案是:, ;
(2)原式=,
=,
=,
=2020;
(3)∵ a,
∴.
∴(a﹣3)2=10,即a2﹣6a+9=10.
∴ a2﹣6a=1,
∴ 2a2﹣12a﹣5=2(a2﹣6a)﹣5=2×1﹣5=﹣3.
25. 如图,直线的解析式为,与轴交于点,直线经过点,与直线交于点,且与轴交于点
(1)求点的坐标及直线的解析式;
(2)求的面积.
(3)在上是否存在一点,使的面积是面积的?若存在,请写出满足条件的所有点的坐标;若不存在,请说明理由.
解:(1)在中,当时,,
,
设直线的解析式为:,
将,代入得:,
解得:,
直线的解析式为;
(2)在中,当时,,解得:,
,
在中,当时,,解得:,
,
,
;
(3)的面积是面积的,
,
,
,
或,
当时,,解得:,即,
当时,,解得:,即,
综上所述,在上存在一点,使的面积是面积的,或.
相关试卷
这是一份2023-2024学年山东省青岛市崂山区八年级(上)期末数学试卷(解析版),共19页。试卷主要包含了选择题,填空题,作图题,解答题等内容,欢迎下载使用。
这是一份2023-2024学年山东省青岛市崂山区九年级(上)期末数学试卷,共4页。
这是一份山东省青岛市崂山区2023-2024学年八年级(上)期中数学试卷,共24页。试卷主要包含了选择题,填空题,作图题,解答题等内容,欢迎下载使用。












