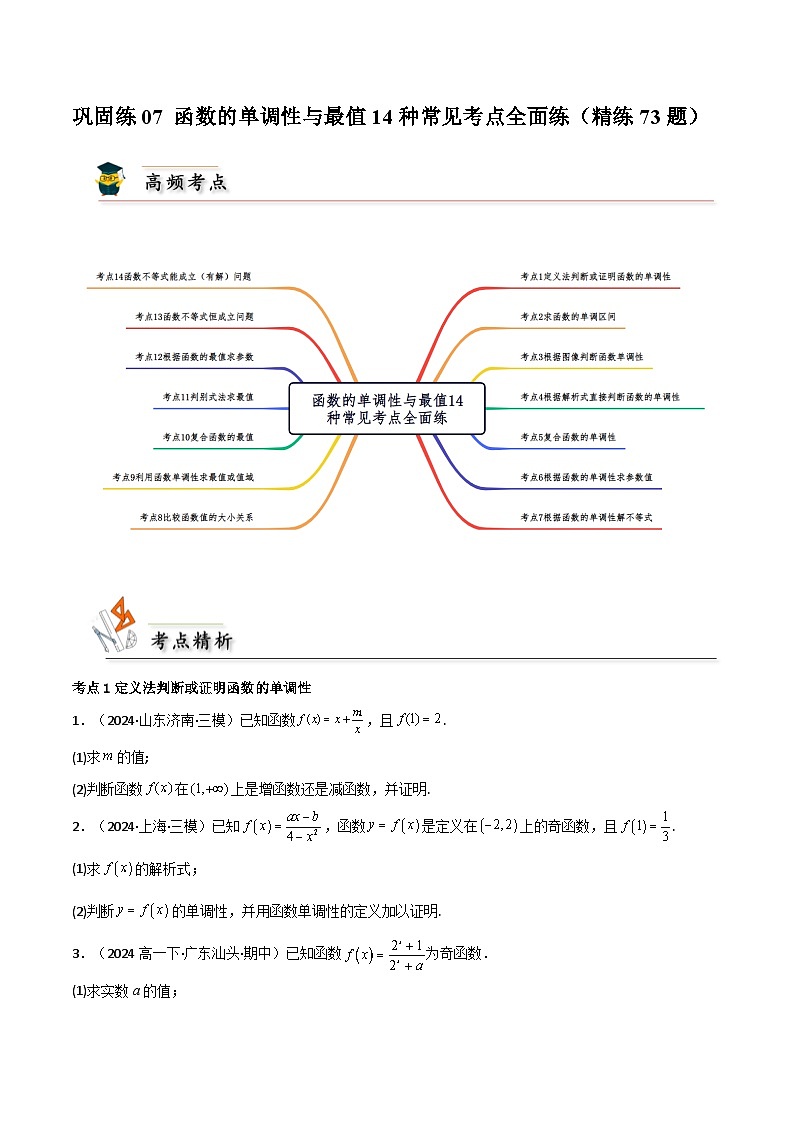
2025高考数学【考点通关】考点归纳与解题策略巩固练07函数的单调性与最值14种常见考点全面练(精练73题)(原卷版+解析)

这是一份2025高考数学【考点通关】考点归纳与解题策略巩固练07函数的单调性与最值14种常见考点全面练(精练73题)(原卷版+解析)，共60页。试卷主要包含了已知函数，且.，已知函数为奇函数，已知奇函数的定义域为.等内容，欢迎下载使用。

考点1定义法判断或证明函数的单调性
1．（2024·山东济南·三模）已知函数，且.
(1)求的值;
(2)判断函数在上是增函数还是减函数，并证明.
2．（2024·上海·三模）已知，函数是定义在上的奇函数，且.
(1)求的解析式；
(2)判断的单调性，并用函数单调性的定义加以证明.
3．（2024高一下·广东汕头·期中）已知函数为奇函数．
(1)求实数a的值；
(2)判断函数的单调性（不用证明）；
(3)设函数，若对任意的，总存在，使得成立，求实数m的取值范围．
4．（2024高二下·陕西西安·阶段练习）已知奇函数的定义域为.
(1)求实数的值；
(2)判断函数的单调性，并用定义证明；
(3)存在，使得成立，求实数m的取值范围．
考点2求函数的单调区间
5．（2024·湖南岳阳·模拟预测）已知函数，则下列结论错误的是（ ）
A．B．的零点为3
C．在上为增函数D．的定义域为
6．（2024·江西·二模）已知函数若，则的单调递增区间为（ ）
A．B．
C．D．
7．（2024·全国·模拟预测）已知函数，则（ ）
A．在单调递增B．在单调递减
C．的图象关于直线对称D．的图象关于点对称
8．（2024·广东深圳·三模）函数的单调递增区间是 ．
9．（2024·全国·三模）函数的单调递减区间为 ．
考点3根据图像判断函数单调性
10．（2024高一上·福建泉州·阶段练习）如图所示是函数的图象，图中曲线与直线无限接近但是永不相交，则以下描述正确的是（ ）
A．函数的定义域为
B．函数的值域为
C．此函数在定义域中不单调
D．对于任意的，都有唯一的自变量x与之对应
11．（2024·辽宁丹东·二模）设函数由关系式确定，函数，则（ ）
A．为增函数B．为奇函数
C．值域为D．函数没有正零点
12．（2024·贵州·模拟预测）已知函数，下列结论正确的是（ ）
A．是偶函数
B．在上单调递增
C．的图象关于直线对称
D．的图象与轴围成的三角形面积为2
13．（2024高三上·广西·学业考试）在2小时内将某种药物注射进患者的血液中，在注射期间，血液中的药物含量呈线性增加；停止注射后，血液中药物含量呈指数衰减，能反映血液中药物含量Q随时间t变化的图象是（ ）
A． B． C． D．
考点4根据解析式直接判断函数的单调性
14．（24-25高一上·全国·随堂练习）函数在上的最小值为（ ）
A．1B．C．D．
15．（24-25高三上·甘肃天水·阶段练习）下列函数中，是偶函数且在上单调递减的是（ ）
A．B．
C．D．
16．（2024高一上·北京·期中）下列函数中，在区间上是减函数的是（ ）
A．B．
C．D．
17．（2024高二下·云南·学业考试）下列函数中，在上单调递增的是（ ）
A．B．
C．D．
考点5复合函数的单调性
18．（2024高三·全国·专题练习）函数的单调递增区间为（ ）
A．B．C．D．
19．（2024高一上·全国·课后作业）函数的单调递增区间为（ ）
A．B．
C．D．
20．（2024高三上·广东湛江·开学考试）已知函数，则的增区间为（ ）
A．B．C．D．
21．（2024高一上·北京·阶段练习）函数单调递增的区间是 .
考点6根据函数的单调性求参数值
22．（2024·广东揭阳·二模）已知函数在上不单调，则的取值范围为（ ）
A．B．
C．D．
23．（2024·天津河北·一模）设，则“”是“函数在上单调递增”的（ ）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
24．（2024·山东·二模）已知函数在区间上单调递增，则的取值范围是（ ）．
A．7,+∞B．
C．D．
25．（2024·黑龙江·模拟预测）设函数在区间上单调递减，则的取值范围是（ ）
A．B．C．D．
26．（2024·黑龙江哈尔滨·模拟预测）若函数在上单调递增，则实数的取值范围为（ ）
A．B．C．D．
27．（2024·陕西榆林·一模）已知函数在上单调递增，则的取值范围是（ ）
A．B．C．D．
28．（2024·陕西安康·模拟预测）已知函数是上的单调函数，则实数的取值范围是（ ）
A．B．C．D．
29．（2024·江苏无锡·二模）已知函数满足对任意的，都有成立，则实数的取值范围为 .
30．（2024·辽宁·三模）已知函数存在两个极值点，若对任意满足的，均有，则实数的取值范围为（ ）
A．B．
C．D．
考点7根据函数的单调性解不等式
31．（2024高三下·山西·阶段练习）已知函数fx=lg2x,02，若fa+1−f2a−1≥0，则实数a的取值范围是（ ）
A．B．C．D．
32．（2024·陕西商洛·三模）已知为偶函数，且在上单调递增，若，则实数的取值范围是（ ）
A．B．C．D．
33．（2024·黑龙江大庆·三模）已知函数fx=2x,x≥0x3+1,x0，⇒12