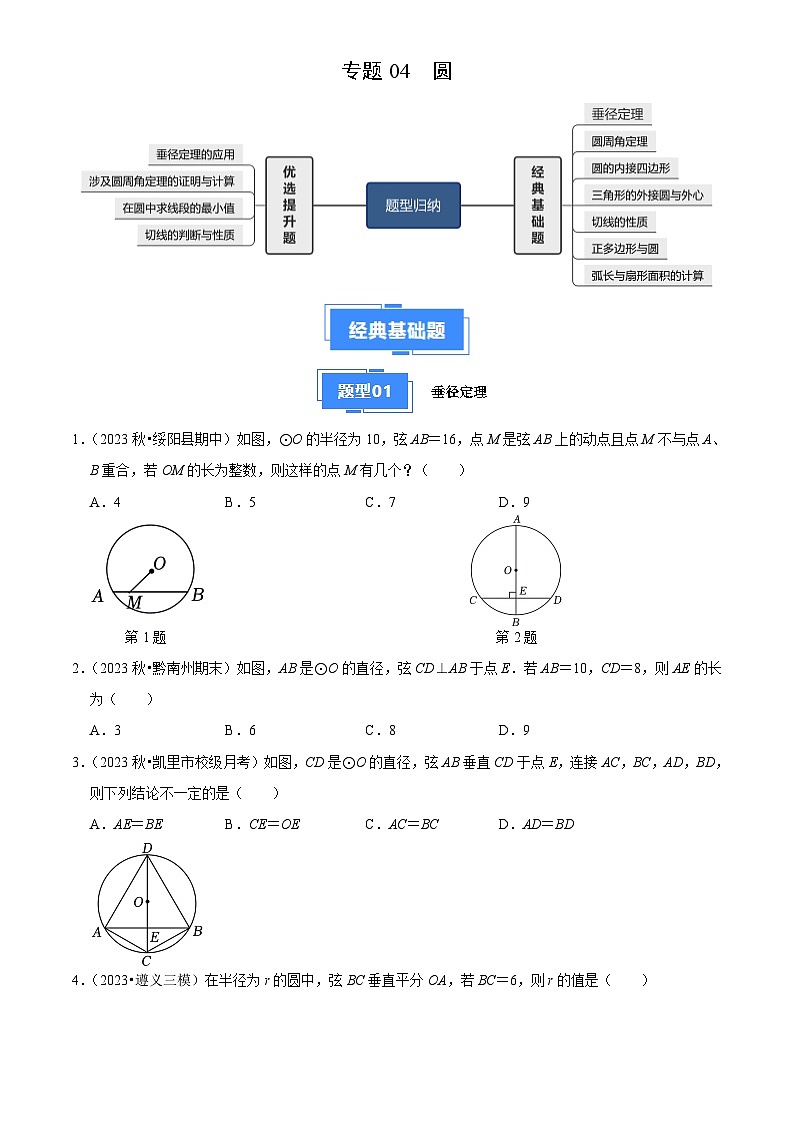




专题04 圆(7大基础题+4大提升题)2024-2025学年九年级数学上学期期中真题分类汇编
展开垂径定理
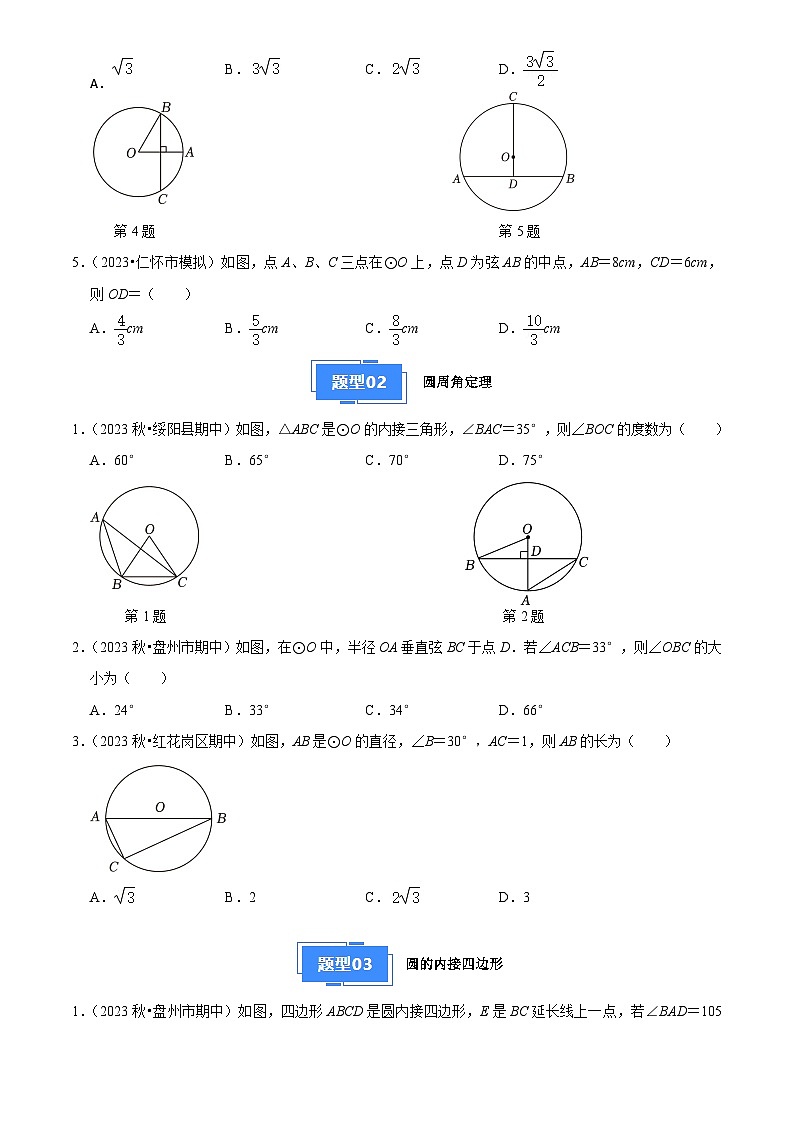
1.(2023秋•绥阳县期中)如图,⊙O的半径为10,弦AB=16,点M是弦AB上的动点且点M不与点A、B重合,若OM的长为整数,则这样的点M有几个?( )
A.4B.5C.7D.9
第1题 第2题
2.(2023秋•黔南州期末)如图,AB是⊙O的直径,弦CD⊥AB于点E.若AB=10,CD=8,则AE的长为( )
A.3B.6C.8D.9
3.(2023秋•凯里市校级月考)如图,CD是⊙O的直径,弦AB垂直CD于点E,连接AC,BC,AD,BD,则下列结论不一定的是( )
A.AE=BEB.CE=OEC.AC=BCD.AD=BD
4.(2023•遵义三模)在半径为r的圆中,弦BC垂直平分OA,若BC=6,则r的值是( )
B.C.D.
第4题 第5题
5.(2023•仁怀市模拟)如图,点A、B、C三点在⊙O上,点D为弦AB的中点,AB=8cm,CD=6cm,则OD=( )
A.cmB.cmC.cmD.cm
圆周角定理
1.(2023秋•绥阳县期中)如图,△ABC是⊙O的内接三角形,∠BAC=35°,则∠BOC的度数为( )
A.60°B.65°C.70°D.75°
第1题 第2题
2.(2023秋•盘州市期中)如图,在⊙O中,半径OA垂直弦BC于点D.若∠ACB=33°,则∠OBC的大小为( )
A.24°B.33°C.34°D.66°
3.(2023秋•红花岗区期中)如图,AB是⊙O的直径,∠B=30°,AC=1,则AB的长为( )
A.B.2C.D.3
圆的内接四边形
1.(2023秋•盘州市期中)如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若∠BAD=105°,则∠DCE的大小是 .
第1题 第2题
2.(2023秋•关岭县期末)如图,四边形ABCD是⊙O的内接四边形,若∠A=110°,则∠BOD的度数为( )
A.40°B.70°C.110°D.140°
3.(2024•息烽县一模)如图,四边形ABCD是⊙O的内接四边形,延长BC到点E,则∠A与∠DCE的数量关系一定成立的是( )
A.∠A=∠DCEB.∠A+∠DCE=180°
C.∠A+∠DCE=90°D.∠A>∠DCE
第3题 第4题
4.(2024•金沙县一模)如图,∠DCE是⊙O内接四边形ABCD的一个外角,若∠DCE=80°,那么∠BOD的度数为( )
A.160°B.135°C.80°D.40°
三角形的外接圆与外心
1.(2023秋•绥阳县期末)在△ABC中,∠C=90°,AC=1,BC=2,M是AB的中点,以点C为圆心,1为半径作⊙C,则( )
A.点M在⊙C外B.点M在⊙C上C.点M在⊙C内D.不能确定
2.(2023秋•遵义期末)如图,⊙O是△PAB的外接圆,OC⊥AB,连接OB.若∠BOC=50°,则∠APB的度数是( )
A.45°B.50°C.55°D.60°
第2题 第3题 第4题
3.(2024•遵义二模)如图,已知点O是△ABC的外心,连接OA,OB,OC,若∠1=40°,则∠BAC的度数为( )
A.20°B.30°C.40°D.50°
4.(2023•钟山区一模)如图,△ABC和△BCD内接于⊙O,AC与BD相交于点E.若AB∥CD,∠A=43°,则∠BEC的度数为 .
5.(2023秋•黔东南州期末)如图,⊙O是△ABC的外接圆,AD是⊙O的直径,AD⊥BC于点E.
(1)求证:∠BAD=∠CAD;
(2)连接BO并延长,交⊙O于点G,连接GC,若OE=3,求GC的长.
切线的性质
1.(2023秋•红花岗区期中)如图,AB是⊙O的直径,BC是⊙O的切线,连接AC交⊙O于点D,连接BD,若∠CBD=28°,则∠A的度数为( )
A.62°B.30°C.28°D.14°
第1题 第2题
2.(2023秋•关岭县期末)如图,将量角器和含30°角的一块直角三角板紧靠着放在同一平面内,使D、C、B在一条直线上,且DC=2BC,过点A作量角器圆弧所在圆的切线,切点为E,则∠EAC的度数是( )
A.60°B.45°C.30°D.50°
3.(2023秋•凯里市校级月考)如图,BC是⊙O的切线,点B是切点,连接CO交⊙O于点D,延长CO交⊙O于点A,连接AB,若∠C=30°,OD=2,则AB的长为( )
A.B.C.D.
第3题 第4题
4.(2023秋•黔南州期末)如图,PA,PB与⊙O分别相切于点A,B,PA=2,∠P=60°,则AB=( )
A.B.2C.D.3
正多边形与圆
1.(2024•黔南州一模)如图,正六边形ABCDEF内接于⊙O,P为上的一点(点P不与点A,B重合),则∠CPE的度数为( )
A.45°B.55°C.60°D.65°
2.(2024•榕江县校级二模)如图,正五边形ABCDE内接于⊙O,连接AC,则∠BAC的度数是( )
A.45°B.38°C.36°D.30°
第2题 第3题 第4题
3.(2024•榕江县校级二模)如图,正六边形ABCDEF的边CD,EF与⊙O相切于点C,F,连接OF,CO,则∠COF的度数是( )
A.120°B.144°C.150°D.160°
4.(2024•仁怀市模拟)如图,若干个全等的正五边形排成环状,图中所示的是前3个正五边形,要完成这一圆环还需正五边形的个数为( )
A.10B.9C.8D.7
弧长与扇形的面积计算
1.(2022•云岩区一模)制作弯形管道时,需要先按中心线计算“展直长度”再下料.试计算如图所示的管道的展直长度,即的长为( )
A.300πmmB.60πmmC.40πmmD.20πmm
2.(2024•从江县校级二模)将一个半径为1的圆形纸片,按如图所示的方式连续对折三次之后,用剪刀沿虚线①剪开,则虚线①所对的圆弧长为( )
A.B.C.D.π
3.(2024•贵州)如图,在扇形纸扇中,若∠AOB=150°,OA=24,则的长为( )
A.30πB.25πC.20πD.10π
第3题 第5题 第7题
4.(2023秋•红花岗区校级期中)若扇形的半径是12cm弧长是20πcm,则扇形的面积为( )
A.120πcm2B.240πcm2C.360πcm2D.60πcm2
5.(2023秋•关岭县期末)中国美食讲究色香味美,优雅的摆盘也会让美食锦上添花,如图①中的摆盘,其形状是扇形的一部分,图②是其几何示意图(阴影部分为摆盘),通过测量得到AC=BD=10cm,OC=OD=3cm,圆心角为60°,则图②中摆盘的面积是( )
A.πcm2B.πcm2C.πcm2D.πcm2
6.(2023秋•七星关区期末)一个扇形的面积是3π cm2,圆心角是120°,则此扇形的半径是 cm.
7.(2023秋•毕节市校级期末)如图,以O为圆心的扇形AOB与扇形COD的圆心角为30°,若AC=2,OC=6,则阴影部分的面积为 .
垂径定理的应用
1.(2023秋•红花岗区期中)“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问:径几何?”转化为现在的数学语言表达就是:如图,CD为⊙O的直径,弦AB⊥CD,垂足为E,CE=1寸,AB=10寸,则直径CD的长度为 寸.
第1题 第2题
2.(2023•遵义模拟)为测量一铁球的直径,将该铁球放入工件槽内,测得有关数据如图所示(单位:cm),则该铁球的直径为 .
2.(2023秋•绥阳县期中)石拱桥是我国古代人民勤劳和智慧的结晶(如图1),隋代建造的赵州桥距今约有1400年历史,是我国古代石拱桥的代表.如图2是根据某石拱桥的实物图画出的几何图形,桥的主桥拱是圆弧形,表示为.桥的跨度(弧所对的弦长)AB=24m,设所在圆的圆心为O,半径OC⊥AB,垂足为D.拱高(弧的中点到弦的距离)CD=5m.连接OB.求这座石拱桥主桥拱的半径.(精确到1m).
涉及圆周角定理的证明与计算
1.(2023秋•红花岗区期中)如图,在△ABC中,CB与⊙O相交于D,CA与⊙O相交于E.
(1)从下面①②③中选取两个作为已知条件,另一个作为结论,并证明;
①AB是直径;
②AC=AB;
③DC=DB.
(2)在(1)的条件下,若BC=6,AB=5,连接BE,求BE的长.
2.(2023秋•关岭县期末)如图,AB为⊙O的直径,点C,D为直径AB同侧圆上的点,且点D为的中点,过点D作DE⊥AB于点E,延长DE,交⊙O于点F,AC与DF交于点G.
(Ⅰ)如图①,若点C为的中点,求∠AGF的度数;
(Ⅱ)如图②,若AC=12,AE=3,求⊙O的半径.
在圆中求线段的最小值
1.(2023秋•红花岗区期中)在矩形ABCD中,AB=2,,点E,F分别是边AD和BC上的动点,且AE=CF,连接EF,过点B作BG⊥EF,垂足为点G,连接CG,则CG的最小值为 .
2.(2023秋•关岭县期末)如图,在Rt△ABC中,∠C=90°,AC=20,BC=24,点D为线段BC上一动点.以CD为⊙O直径,作AD交⊙O于点E,连BE,则BE的最小值为 .
第2题 第3题
3.(2023秋•黔东南州期末)在矩形ABCD中,AB=3,BC=4,点M是平面内一动点,且满足BM=2,N为MD的中点,点M运动过程中线段CN长度的取值范围是 .
切线的判定与性质
1.(2023秋•灵宝市期中)如图,以四边形ABCD的对角线BD为直径作圆,圆心为O,过点A作AE⊥CD的延长线于点E,已知DA平分∠BDE.
(1)求证:AE是⊙O切线;
(2)若AE=4,CD=6,求⊙O的半径和AD的长.
2.(2023秋•红花岗区校级期中)如图,在Rt△ABC中,∠C=90°,点D,E,F分别是边AB,BC,AC上的点,以AD为直径的半圆O经过点E,F,且.
(1)求证:BC是半圆O的切线;
(2)若∠B=30°,AB=12,求CF的长.
3.(2023秋•绥阳县期末)如图,AB为⊙O的直径,OC⊥AB交⊙O于点C,D为OB上一点,延长CD交⊙O于点E,延长OB至F,使DF=FE,连接EF.
(1)求证:EF为⊙O的切线;
(2)若OD=1且BD=BF,求⊙O的半径.
4.(2023秋•黔南州期末)如图,在Rt△ABC中,∠C=90°,以AC为直径的⊙O交AB于点E,D是BC上一点,连接DE,且∠B=∠BED.
(1)求证:ED是⊙O的切线;
(2)若BE=16,ED=10,求AC的长.
专题01 一元二次方程(5大基础题+4大提升题)2024-2025学年九年级数学上学期期中真题分类汇编: 这是一份专题01 一元二次方程(5大基础题+4大提升题)2024-2025学年九年级数学上学期期中真题分类汇编,文件包含专题01一元二次方程5大基础题+4大提升题原卷版docx、专题01一元二次方程5大基础题+4大提升题解析版docx等2份试卷配套教学资源,其中试卷共36页, 欢迎下载使用。
专题03 轴对称(6大基础题+4大提升题))-2024-2025学年八年级数学上学期期中真题分类汇编: 这是一份专题03 轴对称(6大基础题+4大提升题))-2024-2025学年八年级数学上学期期中真题分类汇编,文件包含专题03轴对称6大基础题+4大提升题原卷版docx、专题03轴对称6大基础题+4大提升题解析版docx等2份试卷配套教学资源,其中试卷共45页, 欢迎下载使用。
专题04 选择基础题四-备战宁波中考数学真题模拟题分类汇编: 这是一份专题04 选择基础题四-备战宁波中考数学真题模拟题分类汇编,文件包含专题04选择基础题四-备战宁波中考数学真题模拟题分类汇编解析版docx、专题04选择基础题四-备战宁波中考数学真题模拟题分类汇编原卷版docx等2份试卷配套教学资源,其中试卷共27页, 欢迎下载使用。












