2023-2024学年浙江省金华市婺城区八年级上学期期末数学试题及答案

这是一份2023-2024学年浙江省金华市婺城区八年级上学期期末数学试题及答案，共26页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．（3分）下列“祝你成功”的首拼字母中，属于轴对称图形的是（ ）
A．B．C．D．
2．（3分）在平面直角坐标系中，点P（﹣3，2）在（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
3．（3分）已知一个等腰三角形的周长为10，腰长为4，则它的底边长为（ ）
A．2B．3C．4D．6
4．（3分）不等式2x＜x﹣1的解集在数轴上表示正确的是（ ）
A．B．
C．D．
5．（3分）如图，已知AB＝AD，添加下列一个条件后，仍无法判定△ABC≌△ADC的是（ ）
A．CB＝CDB．∠BCA＝∠DCAC．∠BAC＝∠DACD．∠B＝∠D＝90°
6．（3分）能说明“三角形的高线一定在三角形的内部（含边界）”是假命题的反例是（ ）
A．B．
C．D．
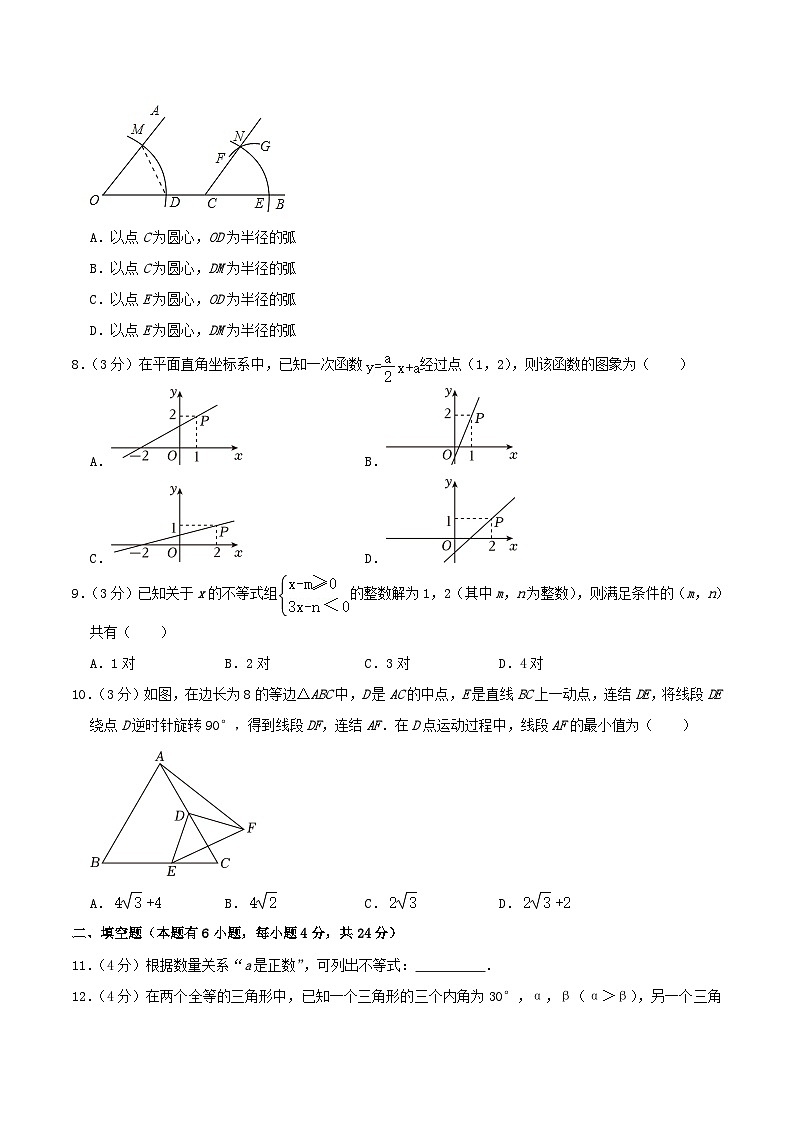
7．（3分）如图，点C在∠AOB的边OB上，用尺规作出了∠BCN＝∠AOC，作图痕迹中，弧FG是（ ）
A．以点C为圆心，OD为半径的弧
B．以点C为圆心，DM为半径的弧
C．以点E为圆心，OD为半径的弧
D．以点E为圆心，DM为半径的弧
8．（3分）在平面直角坐标系中，已知一次函数经过点（1，2），则该函数的图象为（ ）
A．B．
C．D．
9．（3分）已知关于x的不等式组的整数解为1，2（其中m，n为整数），则满足条件的（m，n）共有（ ）
A．1对B．2对C．3对D．4对
10．（3分）如图，在边长为8的等边△ABC中，D是AC的中点，E是直线BC上一动点，连结DE，将线段DE绕点D逆时针旋转90°，得到线段DF，连结AF．在D点运动过程中，线段AF的最小值为（ ）
A．B．C．D．
二、填空题（本题有6小题，每小题4分，共24分）
11．（4分）根据数量关系“a是正数”，可列出不等式： ．
12．（4分）在两个全等的三角形中，已知一个三角形的三个内角为30°，α，β（α＞β），另一个三角形有一个角为70°，则α﹣β＝ °．
13．（4分）小莹按照如图所示的步骤折叠A4纸，折完后，发现折痕AB′与A4纸的长边AB恰好重合，那么A4纸的长AB与宽AD的比值为 ．
14．（4分）剪纸艺术是最古老的中国民间艺术之一，很多剪纸作品体现了数学中的对称美．如图，蝴蝶剪纸是一幅轴对称图形，将其放在平面直角坐标系中，点E的坐标为（﹣2，﹣n），其关于y轴对称的点F的坐标（2，﹣m+1），则（n﹣m）2023＝ ．
15．（4分）如图，将长方形ABCD放置于平面直角坐标系中，点C在第一象限，点A与坐标原点重合，过点A的直线y＝kx交BC于点E，连结DE，已知BE：CE＝1：4，AE平分∠BED，则k的值为 ．
16．（4分）图1是由5个全等的直角三角形与一个小正方形组成，延长DK交AB、AC分别于点M、N，延长EH交BD于点P（如图2）．
（1）若Rt△ABF的面积为5，小正方形FGHK的面积为9，则AB＝ ；
（2）如图2，若，则＝ （用含k的代数式表示）．
三、解答题（本题有8小题，共66分）
17．（6分）解不等式组：．
18．（6分）如图1，在3×3的网格中，△ABC三个顶点均在格点上，这样的三角形叫做“格点三角形”．在图中画出一个“格点三角形”（阴影部分）与原△ABC关于某条直线成轴对称．请在图2、图3、图4中，各画一个和原三角形成轴对称的“格点三角形”，并将所画的“格点三角形”用“斜线”涂成“阴影部分”（图1﹣图4不重复）．
19．（6分）某数学兴趣小组开展测量学校旗杆的实践活动．
【实践发现】数学兴趣小组实地勘查发现：系在旗杆顶端的绳子垂到了地面，并多出了一段，但这条绳子的长度未知．
【实践探究】设计测量方案：
第一步：先测量比旗杆多出的部分绳子的长度，测得多出部分绳子的长度是1米；
第二步：如图，把绳子向外拉直，绳子的底端恰好接触地面的点C，再测量绳子底端C与旗杆AB的底部（点B）之间的距离为5米．
【问题解决】求旗杆的高度．
20．（8分）如图，在△ABC中，∠ABC＝45°，F是高AD和高BE的交点．
（1）求证：∠1＝∠2．
（2）写出图中的一对全等三角形，并给出证明．
21．（8分）已知实数x，y满足3x+2y＝18．
（1）用含x的代数式表示y，则y＝ ．
（2）若等腰三角形的腰长为x，底边长为y，该等腰三角形的周长为l．
①求l关于x的函数表达式；
②求l的取值范围．
22．（10分）【情境建模】我们知道“等腰三角形底边上的高线、中线和顶角平分线重合”，简称“三线合一”．小明尝试着逆向思考：如图1，点D在△ABC的边BC上，给出下列三个条件：①AD平分∠BAC；②AD⊥BC；③BD＝CD．由哪两个条件可以判定AB＝AC？（用序号写出所有成立的情形）
【推理论证】请选择上述情形中的一种情况，给出证明．
【应用内化】如图2，在△ABC中，BC＝a，AC＝b，CD是角平分线，过点A作CD的垂线交CD、BC分别于点E、F．若∠CAF＝2∠B，则BF＝ ；AE＝ ．（结果用含a，b的代数式表示）．
23．（10分）根据以下素材，探索完成任务：
24．（12分）如图，在平面直角坐标系中，过点A（﹣2，0）的直线y＝3x+b与y轴交于点B，直线BC交x轴正半轴于点C，OC＝OB，点P是直线BC上的动点．
（1）求直线BC的解析式．
（2）若，求点P的坐标．
（3）已知点Q在线段AB上，连结OP、OQ、PQ．
①若△PQB与△PQO全等，求线段PQ的长；
②在P、Q的运动过程中，OQ+PQ的最小值为 （直接写出答案）．
参考答案与试题解析
一、选择题（本题有10小题，每小题3分，共30分）
1．（3分）下列“祝你成功”的首拼字母中，属于轴对称图形的是（ ）
A．B．C．D．
【分析】如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，根据轴对称图形的概念求解．
【解答】解：A．不是轴对称图形，故本选项不合题意；
B．不是轴对称图形，故本选项不合题意；
C．是轴对称图形，故本选项符合题意；
D．不是轴对称图形，故本选项不合题意．
故选：C．
2．（3分）在平面直角坐标系中，点P（﹣3，2）在（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【分析】根据各象限内点的坐标特征解答即可．
【解答】解：点P（﹣3，2）在第二象限，
故选：B．
3．（3分）已知一个等腰三角形的周长为10，腰长为4，则它的底边长为（ ）
A．2B．3C．4D．6
【分析】由已知条件，根据等腰三角形的性质及周长公式即可求得其底边长．
【解答】解：因为等腰三角形的周长为10，其腰长为4，
所以它的底边长为10﹣4﹣4＝2．
故选：A．
4．（3分）不等式2x＜x﹣1的解集在数轴上表示正确的是（ ）
A．B．
C．D．
【分析】根据解一元一次不等式基本步骤：移项、合并同类项可得．
【解答】解：移项，得：2x﹣x＜﹣1，
合并同类项，得：x＜﹣1，
故选：C．
5．（3分）如图，已知AB＝AD，添加下列一个条件后，仍无法判定△ABC≌△ADC的是（ ）
A．CB＝CDB．∠BCA＝∠DCAC．∠BAC＝∠DACD．∠B＝∠D＝90°
【分析】要判定△ABC≌△ADC，已知AB＝AD，AC是公共边，具备了两组边对应相等，故添加CB＝CD、∠BAC＝∠DAC、∠B＝∠D＝90°后可分别根据SSS、SAS、HL能判定△ABC≌△ADC，而添加∠BCA＝∠DCA后则不能．
【解答】解：A、添加CB＝CD，根据SSS，能判定△ABC≌△ADC，
故A选项不符合题意；
B、添加∠BCA＝∠DCA时，不能判定△ABC≌△ADC，
故B选项符合题意；
C、添加∠BAC＝∠DAC，根据SAS，能判定△ABC≌△ADC，
故C选项不符合题意；
D、添加∠B＝∠D＝90°，根据HL，能判定△ABC≌△ADC，
故D选项不符合题意；
故选：B．
6．（3分）能说明“三角形的高线一定在三角形的内部（含边界）”是假命题的反例是（ ）
A．B．
C．D．
【分析】找到三角形的高线在三角形的外部的选项即可．
【解答】解：能说明“三角形的高线一定在三角形的内部（含边界）”是假命题的反例是：
故选：C．
7．（3分）如图，点C在∠AOB的边OB上，用尺规作出了∠BCN＝∠AOC，作图痕迹中，弧FG是（ ）
A．以点C为圆心，OD为半径的弧
B．以点C为圆心，DM为半径的弧
C．以点E为圆心，OD为半径的弧
D．以点E为圆心，DM为半径的弧
【分析】运用作一个角等于已知角可得答案．
【解答】解：根据作一个角等于已知角可得弧FG是以点E为圆心，DM为半径的弧．
故选：D．
8．（3分）在平面直角坐标系中，已知一次函数经过点（1，2），则该函数的图象为（ ）
A．B．
C．D．
【分析】把（1，2）代入y＝x+a，求出a的值，根据图象解答即可．
【解答】解：y＝x+a，经过（1，2），
∴把（1，2）代入y＝x+a，
..2＝+a＝a，
∴a＝，
∴y＝x+，
∴图象过P（1，2）且与y轴交于正半轴．
故选：A．
9．（3分）已知关于x的不等式组的整数解为1，2（其中m，n为整数），则满足条件的（m，n）共有（ ）
A．1对B．2对C．3对D．4对
【分析】根据所给不等式组的整数解为1，2，得出m，n的取值范围，再根据m，n为整数即可解决问题．
【解答】解：解不等式x﹣m≥0得，
x≥m；
解不等式3x﹣n＜0得，
x＜；
因为不等式组的整数解为1，2，
所以0＜m≤1，且2＜，
则0＜m≤1，6＜n≤9．
又因为m，n为整数，
所以m＝1，n＝7，8，9，
所以满足条件的（m，n）共有3对．
故选：C．
10．（3分）如图，在边长为8的等边△ABC中，D是AC的中点，E是直线BC上一动点，连结DE，将线段DE绕点D逆时针旋转90°，得到线段DF，连结AF．在D点运动过程中，线段AF的最小值为（ ）
A．B．C．D．
【分析】连接BD，在BD的延长线上取点M，使得DM＝DC，根据全等三角形的性质可得出点F的运动轨迹，据此可解决问题．
【解答】解：连接BD并延长，在BD的延长线上取点M，使得DM＝DC，连接MF，
由旋转可知，
DE＝DF，∠EDF＝90°，
∴∠EDC+∠CDF＝∠CDF+∠FDM＝90°，
∴∠EDC＝∠FDM．
在△EDC和△FDM中，
，
∴△EDC≌△FDM（SAS），
∴∠DMF＝∠C＝60°，
则点F在与DM夹角为60°的直线上运动．
过点A作MF的垂线，垂足为F′，
当点F在点F′时，AF取得最小值．
延长F′M与AC的延长线交于点N，
∵∠MDN＝90°，∠DMF＝60°，
∴∠MND＝30°．
在Rt△MDN中，
tan30°＝，
∴DN＝，
∴AN＝AD+DN＝4+．
在Rt△ANF′中，
sin30°＝，
∴AF′＝，
即AF的最小值为．
故选：D．
二、填空题（本题有6小题，每小题4分，共24分）
11．（4分）根据数量关系“a是正数”，可列出不等式： ．
【分析】根据a为正数用“＞0”表示．
【解答】解：根据题意得a＞0，
故答案为：a＞0．
12．（4分）在两个全等的三角形中，已知一个三角形的三个内角为30°，α，β（α＞β），另一个三角形有一个角为70°，则α﹣β＝ °．
【分析】根据全等三角形的性质和三角形的内角和定理即可得到结论．
【解答】解：∵在两个全等的三角形中，已知一个三角形的三个内角为30°，α，β（α＞β），另一个三角形有一个角为70°，
∴α＝70°或β＝70°，
当α＝70°，β＝80°，
∵α＞β，
∴这种情况不存在，
当β＝70°，α＝80°，
∴α﹣β＝80°﹣70°＝10°，
故答案为：10．
13．（4分）小莹按照如图所示的步骤折叠A4纸，折完后，发现折痕AB′与A4纸的长边AB恰好重合，那么A4纸的长AB与宽AD的比值为 ．
【分析】由第①次折叠知△AD'B'是等腰直角三角形，由第②次折叠知，AB＝AB'，从而解决问题．
【解答】解：由第②次折叠知，AB＝AB'，
由第①次折叠知，∠B'AB＝45°，
∴△AD'B'是等腰直角三角形，
∴AB'＝AD'，
∴AB与宽AD的比值为，
故答案为：，
14．（4分）剪纸艺术是最古老的中国民间艺术之一，很多剪纸作品体现了数学中的对称美．如图，蝴蝶剪纸是一幅轴对称图形，将其放在平面直角坐标系中，点E的坐标为（﹣2，﹣n），其关于y轴对称的点F的坐标（2，﹣m+1），则（n﹣m）2023＝ ．
【分析】利用关于y轴对称的点纵坐标相同，可得n﹣m＝﹣1，即可求出答案．
【解答】解：∵点E的坐标为（﹣2，﹣n），其关于y轴对称的点F的坐标（2，﹣m+1），
∴﹣n＝﹣m+1，
∴n﹣m＝﹣1，
∴（n﹣m）2023＝（﹣1）2023＝﹣1．
故答案为：﹣1．
15．（4分）如图，将长方形ABCD放置于平面直角坐标系中，点C在第一象限，点A与坐标原点重合，过点A的直线y＝kx交BC于点E，连结DE，已知BE：CE＝1：4，AE平分∠BED，则k的值为 ．
【分析】设BE＝x，则CE＝4x，BE：CE＝1：4，由勾股定理求出CD计算解答即可．
【解答】解：设BE＝x，则CE＝4x，BE：CE＝1：4，
∴AD＝BC＝BE+CE＝5x，
∵AE平分∠BED，
∴∠BEA＝∠DEA，
∵BC∥AD，
∴∠DAE＝∠DEA，
∴AD＝DE＝5x，
在Rt△CDE中，CD＝＝3x，
∴AB＝CD＝3x
∴k＝＝3
故答案为：3．
16．（4分）图1是由5个全等的直角三角形与一个小正方形组成，延长DK交AB、AC分别于点M、N，延长EH交BD于点P（如图2）．
（1）若Rt△ABF的面积为5，小正方形FGHK的面积为9，则AB＝ ；
（2）如图2，若，则＝ （用含k的代数式表示）．
【分析】（1）根据勾股定理求出a和b的等式，即可得到AB；
（2）求出a，b，k之间的关系式，从而求得面积比．
【解答】解：（1）设AF＝EG＝DH＝BK＝BC＝a，FK＝GF＝HG＝HK＝b，
∵若Rt△ABF的面积为5，小正方形FGHK的面积为9，
∴a（a+b）＝5，b2＝9，
∴a2+ab＝10，
∵AB2＝a2+（a+b）2，
∴AB＝＝，
故答案为：；
（2）∵SAEHN＝S△AEG+SAGHN＝+b（a+b）＝，＝，
∴＝k（），
∴（）（b+a）＝0，
∴b＝，
∴＝＝，
故答案为：．
三、解答题（本题有8小题，共66分）
17．（6分）解不等式组：．
【分析】别求出各个不等式的解集，再寻找解集的公共部分即可．
【解答】解：
由①得，x≥3，
由②得，x＜7，
∴不等式组的解集为3≤x＜7．
18．（6分）如图1，在3×3的网格中，△ABC三个顶点均在格点上，这样的三角形叫做“格点三角形”．在图中画出一个“格点三角形”（阴影部分）与原△ABC关于某条直线成轴对称．请在图2、图3、图4中，各画一个和原三角形成轴对称的“格点三角形”，并将所画的“格点三角形”用“斜线”涂成“阴影部分”（图1﹣图4不重复）．
【分析】根据轴对称的性质画图．
【解答】解：如图，
19．（6分）某数学兴趣小组开展测量学校旗杆的实践活动．
【实践发现】数学兴趣小组实地勘查发现：系在旗杆顶端的绳子垂到了地面，并多出了一段，但这条绳子的长度未知．
【实践探究】设计测量方案：
第一步：先测量比旗杆多出的部分绳子的长度，测得多出部分绳子的长度是1米；
第二步：如图，把绳子向外拉直，绳子的底端恰好接触地面的点C，再测量绳子底端C与旗杆AB的底部（点B）之间的距离为5米．
【问题解决】求旗杆的高度．
【分析】设旗杆的高度为x米，则绳子的长度是（x+1）米，在Rt△ABC中，根据勾股定理列出方程，解方程即可．
【解答】解：设旗杆的高度为x米，则绳子的长度是（x+1）米，
在Rt△ABC中，AB＝x米，BC＝5米，
由勾股定理得：AB2+BC2＝AC2，
即x2+52＝（x+1）2，
解得：x＝12，
答：旗杆的高度为12米．
20．（8分）如图，在△ABC中，∠ABC＝45°，F是高AD和高BE的交点．
（1）求证：∠1＝∠2．
（2）写出图中的一对全等三角形，并给出证明．
【分析】（1）根据同角的余角相等解答即可；
（2）根据ASA证明三角形全等即可．
【解答】（1）证明：∵F是高AD和高BE的交点，
∴∠1+∠C＝∠2+∠C＝90°，
∴∠1＝∠2；
（2）解：∵∠ADB＝90°，∠ABC＝45°，
∴BD＝AD，
在△BFD与△CAD中，
，
∴△BFD≌△CAD（ASA）．
21．（8分）已知实数x，y满足3x+2y＝18．
（1）用含x的代数式表示y，则y＝ ．
（2）若等腰三角形的腰长为x，底边长为y，该等腰三角形的周长为l．
①求l关于x的函数表达式；
②求l的取值范围．
【分析】（1）通过移项、合并同类项、系数化为1即可得出y与x的关系式；
（2）①根据三角形周长的计算公式解答即可；
②先求出x的取值范围，即可确定l的取值范围．
【解答】解：（1）3x+2y＝18，
2y＝18﹣3x，
∴y＝9﹣，
故答案为：9﹣；
（2）①由题意得，等腰三角形的周长l＝2x+y，
由（1）得y＝9﹣，
∴l＝2x+9﹣＝；
②由三角形三边关系定理得，2x＞y，
∴2x＞9﹣，
解得，
又∵y＞0，
∴9﹣＞0，
解得x＜6，
∴，
∴．
22．（10分）【情境建模】我们知道“等腰三角形底边上的高线、中线和顶角平分线重合”，简称“三线合一”．小明尝试着逆向思考：如图1，点D在△ABC的边BC上，给出下列三个条件：①AD平分∠BAC；②AD⊥BC；③BD＝CD．由哪两个条件可以判定AB＝AC？（用序号写出所有成立的情形）
【推理论证】请选择上述情形中的一种情况，给出证明．
【应用内化】如图2，在△ABC中，BC＝a，AC＝b，CD是角平分线，过点A作CD的垂线交CD、BC分别于点E、F．若∠CAF＝2∠B，则BF＝ ；AE＝ ．（结果用含a，b的代数式表示）．
【分析】（1）根据角平分线的定义得到∠BAD＝∠CAD，求得∠BDA＝∠CDA＝90°，得到∠B＝∠C，根据等腰三角形的判定定理得到结论；
（2）根据角平分线的定义得到∠ACE＝∠FCE，根据全等三角形的性质得到CF＝AC＝b，∠CAF＝∠CFA，AE＝EF，求得BF＝BC﹣CF＝a﹣b，得到BF＝AF＝a﹣b．于是得到结论．
【解答】解：（1）①②或②③，
证明：∵AD平分∠BAC，
∴∠BAD＝∠CAD，
∵AD⊥BC，
∴∠BDA＝∠CDA＝90°，
∴∠B+∠BAD＝90°，∠C+∠CAD＝90°，
∴∠B＝∠C，
∴AB＝AC；
（2）∵CD是角平分线，
∴∠ACE＝∠FCE，
∵AE⊥CD，
∴∠AEC＝∠CEF＝90°，
在△ACE与△FCE中，
，
∴△ACE≌△FCE（ASA），
∴CF＝AC＝b，∠CAF＝∠CFA，AE＝EF，
∴BF＝BC﹣CF＝a﹣b，
∵∠CAF＝2∠B，
∴∠AFC＝∠B+∠EAB＝2∠B，
∴∠B＝∠FAB，
∴BF＝AF＝a﹣b．
∴AE＝＝．
故答案为：a﹣b，．
23．（10分）根据以下素材，探索完成任务：
【分析】任务一：根据素材1得出谷物、牛奶和鸡蛋中各含蛋白质的百分数，再算出任务一中各食物中蛋白质的含量相加即可；
任务二：设该早餐中牛奶xg，谷物yg，列方程组解答即可；
任务三：设每周共有a天选A套餐，（5﹣a）天选B套餐，根据题意列方程组解答即可．
【解答】解：
任务一：由题意可知：谷物中蛋白质含量9%，牛奶中蛋白质含量3%，鸡蛋中蛋白质含量15%，有：
100×9%+200×3%+60×15%＝24g；
答：该份早餐中蛋白质总含量为24g．
任务二：设该早餐中牛奶xg，谷物yg，列方程组得：
，
解得：，
答：该早餐中牛奶130g，谷物110g．
任务三：设每周共有a天选A套餐，（5﹣a）天选B套餐，根据题意得：
，
解得：，
∴a＝3或a＝4，
当a＝3时，5﹣a＝2，
当a＝4时，5﹣a＝1．
答：每个学生一周内午餐可以选择A套餐3天、B套餐2天或可以选择A套餐4天、B套餐1天．
24．（12分）如图，在平面直角坐标系中，过点A（﹣2，0）的直线y＝3x+b与y轴交于点B，直线BC交x轴正半轴于点C，OC＝OB，点P是直线BC上的动点．
（1）求直线BC的解析式．
（2）若，求点P的坐标．
（3）已知点Q在线段AB上，连结OP、OQ、PQ．
①若△PQB与△PQO全等，求线段PQ的长；
②在P、Q的运动过程中，OQ+PQ的最小值为 （直接写出答案）．
【分析】（1）把点A代入直线y＝3x+b得B（0，6），设直线BC解析式为y＝kx+6，代入B得k＝﹣1，故直线BC的解析式为y＝﹣x+6．
（2）设P（t，﹣t+6），当P在CB延长线上时，S△APC＝S△ABC＝××8×6＝32，再计算即可．当P在线段CB上时，S△APC＝S△ABC＝××8×6＝16，再计算即可．
（3）①当△PQB≌△PQO时，得QP为△BAC中位线，故PQ＝AC＝4．当△PQB≌△QPO时，得四边形BPOQ是平行四边形，由平移得直线OP解析式为y＝3x，直线OQ解析式为y＝﹣x，联立得P（，），Q（﹣，），故PQ＝＝3．
②过O作AB的对称点O'，过O'作O'P⊥BC，连OQ，此时OQ+PQ＝O'Q+PQ＝O'P最小．由Rt△OAK∽Rt△OBA，得AK＝，OK＝，再利用Rt△OAK～Rt△OO'M，得OM＝，O'M＝，故O'（﹣，），N（，），由等腰Rt△得O'P＝，再计算即可．
【解答】解：（1）∵点A（﹣2，0）在直线y＝3x+b上，
∴b＝6，
∴B（0，6），
∵OC＝OB，
∴C（6，0），
设直线BC解析式为y＝kx+6，
∴0＝6k+6，
∴k＝﹣1，
∴直线BC的解析式为y＝﹣x+6．
（2）设P（t，﹣t+6），
当P在CB延长线上时，
∵，
∴S△APC＝S△ABC＝××8×6＝32，
∴×8×（﹣t+6）＝32，
∴t＝﹣2，
∴P（﹣2，8）．
当P在线段CB上时，
∵，
∴S△APC＝S△ABC＝××8×6＝16，
∴×8×（﹣t+6）＝16，
∴t＝2，
∴P（2，4）．
答：P坐标为（﹣2，8）或（2，4）．
（3）①当△PQB≌△PQO时，
∴QB＝QO，
∴∠QBO＝∠QOB，
∵∠QBO+∠BAO＝90°，
∠QOB+∠QOA＝90°，
∴∠BAO＝∠QOA，
∴QA＝QO，
∴QB＝QO，
∴QP为△BAC中位线，
∴PQ＝AC＝4．
②当△PQB≌△QPO时，
∴QB＝PO，且QB∥PO，
∴四边形BPOQ是平行四边形，
∴AB∥OP，OQ∥BC，
∵直线AB解析式为y＝3x﹣2，
∴向右平移两个长度单位为直线OP解析式：y＝3x，
同理，直线OQ解析式为：y＝﹣x，
联立y＝3x﹣2得P（，），
同理：Q（﹣，），
∴PQ＝＝3．
答：线段PQ的长为4或3．
②过O作AB的对称点O'，过O'作O'P⊥BC，连OQ，
此时OQ+PQ＝O'Q+PQ＝O'P最小．
过O'作O'M⊥x轴．
∴Rt△OAK∽Rt△OBA，
∴OA2＝AK•AB，
∴22＝AK•，
∴AK＝，
∴OK＝＝，
∴OO'＝2OK＝，
∵Rt△OAK～Rt△OO'M，
∴，
∴，
∴，O'M＝，
∴O'（﹣，），
∴R的纵坐标，
∴R（，），
∵∠PRO'＝∠BCA＝45°，
∴O'P＝＝＝，
故答案为：．快餐方案的确定
素材1
100g谷物、100g牛奶和100g鸡蛋的部分营养成分见表：
项目
谷物
牛奶
鸡蛋
蛋白质（g）
9.0
3.0
15
脂肪（g）
32.4
3.6
5.2
碳水化合物（g）
50.8
4.5
1.4
素材2
阳光营养餐公司为学生提供的早餐中，蛋白质总含量占早餐总质量的8%．该早餐包含一个60g的鸡蛋、一份牛奶和一份谷物食品．
素材3
阳光营养餐公司为学生提供的午餐有A、B两种套餐（见表）．为了平衡膳食，公司建议控制学生的主食和肉类摄入量，在一周内，每个学生午餐主食的摄入量不超过830g，午餐肉类摄入量不超过410g．
套餐
主食
肉类
其他
A
150g
85g
165g
B
180g
60g
160g
问题解决
任务1
若一份早餐包含一个60g的鸡蛋、200g牛奶和100g谷物食品，求该份早餐中蛋白质总含量为多少g？
任务2
已知阳光快餐公司提供的一份早餐的总质量为300g，则每份早餐中牛奶和谷物食品各多少g？
任务3
为平衡膳食，每个学生一周内午餐可以选择A、B套餐各几天（一周按5天计算）？
快餐方案的确定
素材1
100g谷物、100g牛奶和100g鸡蛋的部分营养成分见表：
项目
谷物
牛奶
鸡蛋
蛋白质（g）
9.0
3.0
15
脂肪（g）
32.4
3.6
5.2
碳水化合物（g）
50.8
4.5
1.4
素材2
阳光营养餐公司为学生提供的早餐中，蛋白质总含量占早餐总质量的8%．该早餐包含一个60g的鸡蛋、一份牛奶和一份谷物食品．
素材3
阳光营养餐公司为学生提供的午餐有A、B两种套餐（见表）．为了平衡膳食，公司建议控制学生的主食和肉类摄入量，在一周内，每个学生午餐主食的摄入量不超过830g，午餐肉类摄入量不超过410g．
套餐
主食
肉类
其他
A
150g
85g
165g
B
180g
60g
160g
问题解决
任务1
若一份早餐包含一个60g的鸡蛋、200g牛奶和100g谷物食品，求该份早餐中蛋白质总含量为多少g？
任务2
已知阳光快餐公司提供的一份早餐的总质量为300g，则每份早餐中牛奶和谷物食品各多少g？
任务3
为平衡膳食，每个学生一周内午餐可以选择A、B套餐各几天（一周按5天计算）？