山东省济南市历城区2023-2024学年七年级上学期期中数学试卷（解析版）

这是一份山东省济南市历城区2023-2024学年七年级上学期期中数学试卷（解析版），共14页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题(本大题共10个小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．)
1. 的相反数是（ ）
A. B. C. 8D.
【答案】C
【解析】的相反数是8，故C符合题意.
故选：C．
2. 如图所示图形绕直线旋转一周，可以得到圆柱的是（ ）
A. B. C. D.
【答案】A
【解析】A、将所示图形绕直线旋转一周，可以得到圆柱，故A符合题意；
B、将所示图形绕直线旋转一周，可以得到球体，故B不符合题意；
C、将所示图形绕直线旋转一周，可以得到圆锥，故C不符合题意；
D．将所示图形绕直线旋转一周，可以得到圆台，故D不符合题意.
故选：A.
3. 2023年10月1日，国庆假期第一天，天下第一泉(济南趵突泉)风景区接待游客超过291200人次．将数字291200用科学记数法表示应为( )
A. B. C. D.
【答案】C
【解析】将数字291200用科学记数法表示应为．
故选：C．
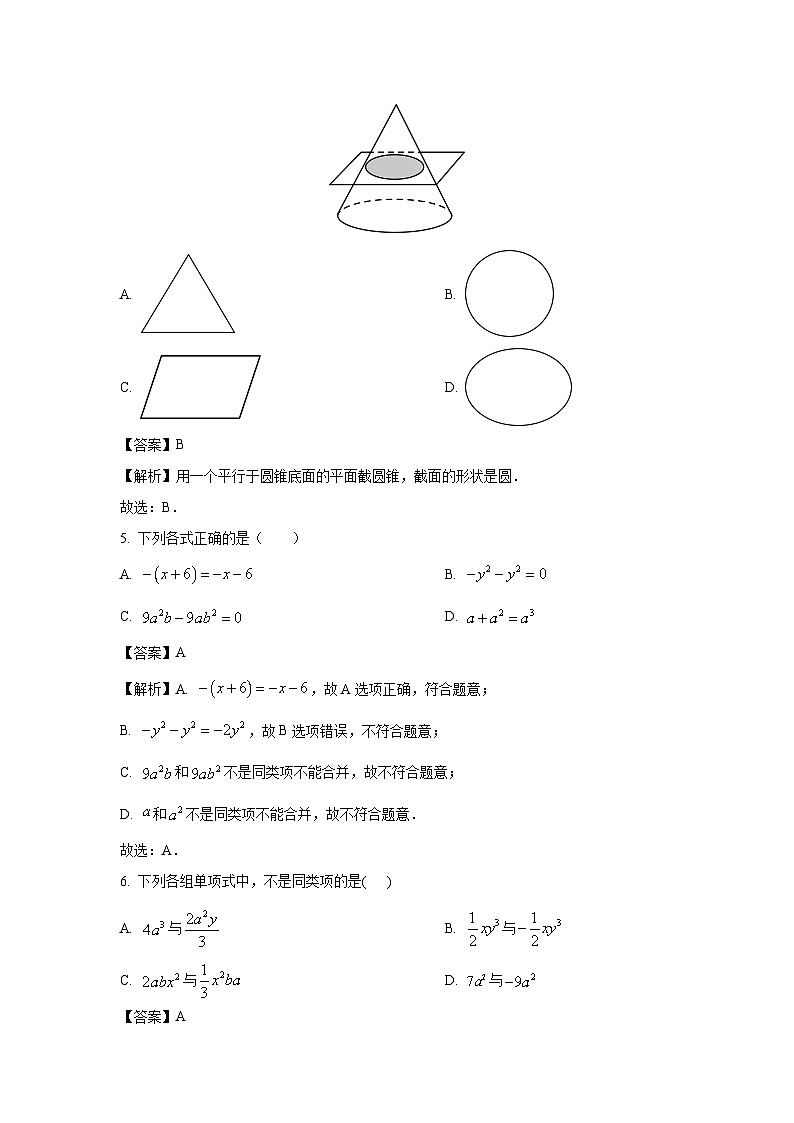
4. 计算机层析成像（CT）技术的工作原理与几何体的切截相似，只不过这里的“截”不是真正的截，“几何体”是病人的患病器官，“刀”是射线．如图，用一个平行于圆锥底面的平面切截圆锥，截面的形状是（ ）
A. B.
C. D.
【答案】B
【解析】用一个平行于圆锥底面的平面截圆锥，截面的形状是圆．
故选：B．
5. 下列各式正确的是（ ）
A. B.
C. D.
【答案】A
【解析】A. ，故A选项正确，符合题意；
B. ，故B选项错误，不符合题意；
C. 和不是同类项不能合并，故不符合题意；
D. 和不是同类项不能合并，故不符合题意．
故选：A．
6. 下列各组单项式中，不是同类项的是( )
A. 与B. 与
C. 与D. 与
【答案】A
【解析】与不是同类项，选项A符合题意；
与是同类项，选项B不符合题意；
与是同类项，选项C不符合题意；
与是同类项，选项D不符合题意.
故选：A．
7. 魏晋时期的数学家刘徽在其著作《九章算术》中用不同颜色的算筹（小棍形状的记数工具）分别表示正数和负数（白色为正，灰色为负），图1表示的是的计算过程，则图2表示的计算过程是（ ）
A. B.
C. D.
【答案】B
【解析】根据题意，图2表示的计算过程是：.
故选：B．
8. 表示有理数a，b的点在数轴上的位置如图所示，以下四个式子中正确的是( )
A. B. C. D.
【答案】D
【解析】，
A、，则，故该项不符合题意；
B、是负数，是正数，则，故该项不符合题意；
C、，则，故该项不符合题意；
D、是负数，是正数，则，故该项符合题意.
故选：D．
9. 下列说法中正确是（ ）
A. 表示负数B. 若，则
C. 单项式系数为D. 多项式的次数是4
【答案】D
【解析】A.当时，，故此项错误；
B.，则，故此项错误；
C.单项式的系数为，故此项错误；
D.的次数是，的次数是，的次数是，
所以多项式的次数是4，故此项正确．
故选：D．
10. 找出如图所示图形变化的规律，则第101个图形中黑色正方形的数量是（ ）
A. 152B. 151C. 150D. 149
【答案】A
【解析】第1个图形中黑色正方形的数量为，
第2个图形中黑色正方形的数量为，
第3个图形中黑色正方形的数量为，
第4个图形中黑色正方形的数量为，
第5个图形中黑色正方形的数量为，
…
∴当为偶数时，第个图形中黑色正方形的数量为个；
当为奇数时第个图形中黑色正方形的数量为个，
∴当时，黑色正方形的个数为个．
故选：A．
二、填空题(本大题共6个小题，每小题4分，共24分．)
11. 若将顺时针旋转记为，则逆时针旋转可记为_____．
【答案】
【解析】若将顺时针旋转记为，则逆时针旋转可记为．
12. 在这四个数中最小的数是______．
【答案】
【解析】，∴最小的数为.
13. 根据如图所示的程序计算，若输入的值为，则输出的值为_____．
【答案】
【解析】依据题中的计算程序列出算式：，
∴应该按照计算程序继续计算，，∴．
14. 若，则代数式的值为______．
【答案】6
【解析】.
15. 一个正方体的六个面分别标有数字1，2，3，4，5，6，从三个不同的方向看到的情形如图1所示，图2为这个正方体的侧面展开图，则图中的x表示的数字是________．
【答案】3
【解析】由图1可知，与1相邻的面的数字有2、3、4、6，的对面数字是5，
与4相邻的面的数字有1、3、5、6，的对面数字是2，的对面数字是6，
由图2可知：6的对面数字是，的值为3.
16. 现有一列数，，，，，，，其中，，，且满足任意相邻三个数的和为同一个常数，则的值为______．
【答案】2035
【解析】由题意得：，∴，
同理可得：，，∴这列数是每三个一循环，
∵，，，∴，，，
∴，
∵，∴.
三、解答题：(本大题共8个小题，共86分．解答应写出文字说明、证明过程或演算步骤．)
17. 计算：
（1）；
（2）；
（3）；
（4）.
解：（1）
.
（2）
.
（3）
.
（4）
.
18. 化简：
（1）；
（2）；
（3）先化简，再求值：，其中，．
解：（1）
.
（2）
.
（3）
，
将，代入中得：.
19. 如图，是一些棱长为的小立方块组成的几何体．
（1）请在上面方格纸中分别画出从左面、上面看到的这个几何体的形状图．
（2）该几何体的体积是______．
解：（1）如图所示：
（2）由题意可知：该几何体由6个小立方体组成，所以该几何体的体积是．
20. 某校举办了“废纸回收，变废为宝”活动，各班收集的废纸均以5kg为标准，超过的记为“＋”，不足的记为“-”，七年级六个班的废纸收集情况如表所示，统计员小虎不小心将一个数据弄脏看不清了，但他记得三班收集废纸最少，且收集废纸最多和最少的班级的质量差为4kg．
（1）请你计算七年级六班同学收集废纸的质量．
（2）若七年级计划总共收集废纸30kg，他们达到预期目标了吗?请说明理由．
（3）若七年级六个班将本次活动收集的废纸集中卖出，30kg(包括30kg)以内的2元/kg，超出30kg的部分2.5 元kg，求废纸卖出的总钱数．
解：（1）经分析，六班收集废纸的质量最多，超出标准质量为：，
六班收集废纸的质量为．
答：六班收集废纸的质量为.
（2）他们达到预期目标，理由：
，
答：他们达到预期目标.
（3）废纸卖出的总钱数为（元．
答：废纸卖出的总钱数为67.5元．
21. 如图所示，在一张正方形纸片的四个角上各剪去一个同样大小的正方形，然后把剩下的部分折成一个无盖的长方体盒子．请回答下列问题：
（1）剪去的小正方形的边长与折成的无盖长方体盒子的高之间的大小关系为________；
（2）如果设原来这张正方形纸片的边长为acm，所折成的无盖长方体盒子的高为hcm，那么这个无盖长方体盒子的容积可以表示为________(用含a，h的代数式表示，无需化简．)
（3）如果原正方形纸片的边长为20cm，剪去的小正方形的边长按整数值依次变化，即分别取1cm，2cm，3cm，4cm，5cm，6cm，7cm，8cm，9cm，10cm 时，计算折成的无盖长方体盒子的容积得到下表，请补全表格．
（4）观察表格，当剪去的小正方形边长为整数，且等于________cm时，折成的无盖长方体盒子的容积最大．
解：（1）由折叠可知，剪去的小正方形的边长与折成的无盖长方体盒子的高之间的大小关系为相等.
（2）这个无盖长方体盒子的容积.
（3）当剪去的小正方形的边长取2时，，
当剪去的小正方形的边长取3时，.
（4）当剪去的小正方形的边长的值逐渐增大时，
所得到的无盖长方体纸盒的容积的值先增大后减小，
当剪去的小正方形的边长为时，所得到的无盖长方体纸盒的容积最大．
22. 如图1，将一个边长为厘米的正方形纸片剪去两个完全相同的小矩形，得到图案，如图2所示，再将剪下的两个小矩形拼成一个新的矩形，如图3所示.
（1）图3中新的矩形的长为__________厘米，宽__________厘米；
（2）求图3中新的矩形的周长．
（3）如果正方形纸片的边长为8厘米，剪去的小矩形的宽为1厘米，求图2的周长
解：（1）新的矩形的长为厘米，宽为厘米.
（2）根据题意，得新的矩形的周长为：厘米．
（3）根据题意，可知，，得．
∴图2的周长为：厘米．
23. 已知，，且的值与的取值无关．
（1）求，的值；
（2）求代数式的值．
解：（1）因为，，
所以
．
因为此多项式的值与字母的取值无关，所以，，
所以，．
（2）．
24. 将一张等边三角形纸片剪成四个大小、形状一样的小等边三角形（如图所示），记为第一次操作，然后将其中右下角的等边三角形又按同样的方法剪成四小片，记为第二次操作，若每次都把右下角的等边三角形按此方法剪成四小片，如此循环进行下去．
（1）如果剪n次共能得到______个等边三角形．
（2）若原等边三角形的边长为1，设表示第n次所剪出的小等边三角形的边长，如．
①试用含的式子表示______；
②计算______；
（3）运用（2）的结论，计算的值．
解：（1）由题意可知：
剪1次共得到的等边三角形个数为：；
剪2次共得到的等边三角形个数为：；
剪3次共得到的等边三角形个数为：；
…，
所以剪n次共得到的等边三角形个数为个．
（2）①因为原等边三角形的边长为1，
所以第1次所剪出的小等边三角形的边长为：；
第2次所剪出的小等边三角形的边长为：；
第3次所剪出的小等边三角形的边长为：；
…，
所以第n次所剪出的小等边三角形的边长为：，即.
②由①题可知：
；
令①，
则②，
②-①得：，
即．
（3）
．
25. 阅读下面材料：若点A，B在数轴上分别表示实数a，b，则A，B两点之间的距离表示为，且回答下列问题；
（1）①数轴上表示x和2的两点A和B之间的距离是______；
②在①的情况下，如果，那么______；
（2）若x为整数，则当代数式取最小值时，满足条件的所有x值为______；
（3）若点A，B，C在数轴上分别表示数a，b，c；a是最大的负整数，且，
①填空： ______； ______； ______；
②点A，B，C同时开始在数轴上运动，若点A以每秒2个单位长度的速度向左运动，同时，点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动，假设运动时间为t秒钟时，点B与点C之间的距离表示为，点A与点B之间的距离表示为．请问：的值是否随着时间t的变化而改变？若变化，请说明理由：若不变，请求其值．
解：（1）①数轴上表示x和2的两点A和B之间的距离：.
②∵，∴，即或，
∴或．
（2）当x在和2之间时，取得最小值3，∴，
∵x为整数，∴x值为，0，1，2．
（3）①∵a是最大的负整数，∴，
∵，∴，
∴.
②的值不随着时间的变化而改变，其值是．
理由如下：
点A以每秒2个单位的速度向左运动，点和点分别以每秒2个单位长度和5个单位长度的速度右运动，
秒时，点A对应的数是，点对应的数是，点对应的数是，
，，
．班级
一
二
三
四
五
六
超过（不足）
0
剪去的小正方形的边长/cm
1
2
3
4
5
6
7
8
9
10
折成的无盖长方体的容积
324
576
500
384
252
128
36
0