2025年中考数学一轮复习《特殊的平行四边形》单元检测卷（含答案）

这是一份2025年中考数学一轮复习《特殊的平行四边形》单元检测卷（含答案），共13页。试卷主要包含了选择题，填空题，解答题，综合题等内容，欢迎下载使用。
在菱形ABCD中，AB＝5，∠B：∠BCD＝1：2，则对角线AC的长等于( )
A.5 B.10 C.15 D.20
将矩形ABCD沿AE折叠，得到如图所示的图形，已知∠CED′＝60°，则∠AED的大小是( )
A.60° B.50° C.75° D.55°
如图，已知菱形ABCD，∠B＝60°，AB＝4，则以AC为边长的正方形ACEF的周长为( )
A.16 B.12 C.24 D.18
如图，丝带重叠的部分一定是（ ）
A.正方形 B.矩形 C.菱形 D.都有可能
对角线相等且互相平分的四边形是( )
A.一般四边形 B.平行四边形 C.矩形 D.菱形
如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB＝BC时,它是菱形
B.当AC⊥BD时,它是菱形
C.当∠ABC＝90°时,它是矩形
D.当AC＝BD时,它是正方形
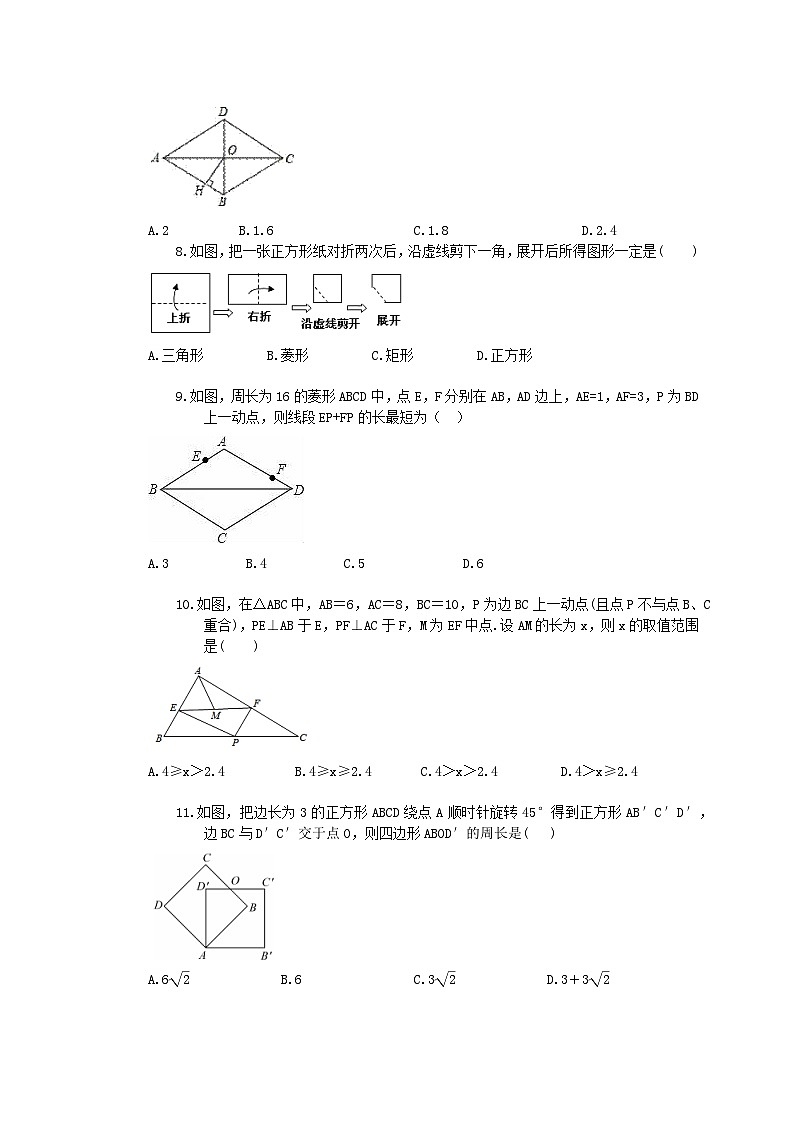
如图，菱形ABCD的对角线AC、BD相交于点O，AC=8，BD=6，过点O作OH⊥AB，垂足为H，则点O到边AB的距离OH等于( )
A.2 B.1.6 C.1.8 D.2.4
如图，把一张正方形纸对折两次后，沿虚线剪下一角，展开后所得图形一定是( )
A.三角形 B.菱形 C.矩形 D.正方形
如图，周长为16的菱形ABCD中，点E，F分别在AB，AD边上，AE=1，AF=3，P为BD上一动点，则线段EP+FP的长最短为（ ）
A.3 B.4 C.5 D.6
如图，在△ABC中，AB＝6，AC＝8，BC＝10，P为边BC上一动点(且点P不与点B、C重合)，PE⊥AB于E，PF⊥AC于F，M为EF中点.设AM的长为x，则x的取值范围是( )
A.4≥x＞2.4 B.4≥x≥2.4 C.4＞x＞2.4 D.4＞x≥2.4
如图，把边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB′C′D′，边BC与D′C′交于点O，则四边形ABOD′的周长是( )
A.6eq \r(2) B.6 C.3eq \r(2) D.3＋3eq \r(2)
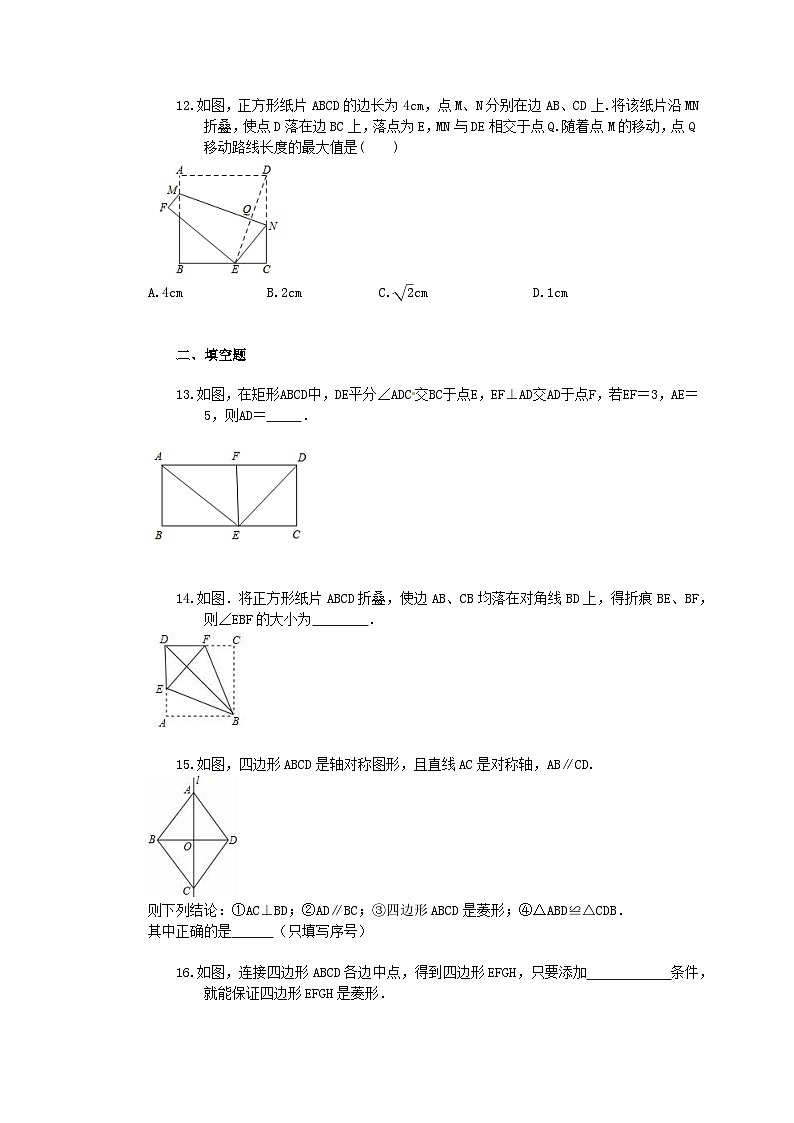
如图，正方形纸片ABCD的边长为4cm，点M、N分别在边AB、CD上.将该纸片沿MN折叠，使点D落在边BC上，落点为E，MN与DE相交于点Q.随着点M的移动，点Q移动路线长度的最大值是( )

A.4cm B.2cm C.eq \r(2)cm D.1cm
二、填空题
如图，在矩形ABCD中，DE平分∠ADC交BC于点E，EF⊥AD交AD于点F，若EF＝3，AE＝5，则AD＝ ．
如图．将正方形纸片ABCD折叠，使边AB、CB均落在对角线BD上，得折痕BE、BF，则∠EBF的大小为 ．
如图，四边形ABCD是轴对称图形，且直线AC是对称轴，AB∥CD.
则下列结论：①AC⊥BD；②AD∥BC；③四边形ABCD是菱形；④△ABD≌△CDB．
其中正确的是 （只填写序号）
如图，连接四边形ABCD各边中点，得到四边形EFGH，只要添加 条件，就能保证四边形EFGH是菱形．
如图，菱形ABCD和菱形ECGF的边长分别为2和3，∠A=120°，则图中阴影部分的面积是_________.
如图，点P的坐标为(2，2)，点A，B分别在x轴，y轴的正半轴上运动，且∠APB＝90°.
下列结论：
①PA＝PB；
②当OA＝OB时四边形OAPB是正方形；
③四边形OAPB的面积和周长都是定值；
④连接OP，AB，则AB＞OP.
其中正确的结论是 .(把你认为正确结论的序号都填上)
三、解答题
如图，在Rt△ABC中，∠ACB＝90°，D为AB的中点，且AE∥CD，CE∥AB．
(1)证明：四边形ADCE是菱形；
(2)若∠B＝60°，BC＝6，求菱形ADCE的高．(计算结果保留根号)
如图，在矩形ABCD中，AD＝12，AB＝7，DF平分∠ADC，AF⊥EF.
(1)求证：AF＝EF；
(2)求EF长.
如图，在正方形ABCD中，E，F分别为AD，CD边上的点，BE，AF交于点O，且AE＝DF．
(1)求证：△ABE≌△DAF；
(2)若BO＝4，DE＝2，求正方形ABCD的面积．
如图，在矩形ABCD中，沿EF将矩形折叠，使A、C重合，AC与EF交于点H.
(1)求证：△ABE≌△AGF；
(2)若AB＝6，BC＝8，求△ABE的面积．
如图，在矩形ABCD中，对角线BD的垂直平分线MN与AD相交于点M，与BC相交于点N，连接BM，DN.
(1)求证：四边形BMDN是菱形；
(2)若AB＝4，AD＝8，求MD的长.
四、综合题
如图1，已知四边形ABCD中，∠ABC＝135°，连接AC、BD，交于点E，BD⊥BC，AD＝AC
(1)求证：∠DAC＝90°；
(2)如图2，过点B作BF⊥AB，交DC于点F，交AC于点G，若S△DBF＝2S△CBF，求证：AG＝CG；
(3)如图3，在(2)的条件下，若AB＝3，求线段GF的长.
四边形ABCD为正方形，点E为线段AC上一点，连接DE，过点E作EF⊥DE，交射线BC于点F，以DE、EF为邻边作矩形DEFG，连接CG
(1)如图，求证：矩形DEFG是正方形；
(2)若AB＝2eq \r(2)，CE＝2，求CG的长；
(3)当线段DE与正方形ABCD的某条边的夹角是40°时，直接写出∠EFC的度数．
\s 0 2025年中考数学一轮复习《特殊的平行四边形》单元检测卷（含答案）答案解析
一、选择题
A
A
A.
C.
C.
D
D
B.
B
C.
A
B；
二、填空题
答案为：7.
答案为：45°．
答案为：①②③④．
答案为：AC＝BD．
答案为：
答案为：①②.
三、解答题
证明：(1)∵AE∥CD，CE∥AB，
∴四边形ADCE是平行四边形，
又∵∠ACB＝90°，D是AB的中点，
∴CD＝eq \f(1,2)AB＝BD＝AD，
∴平行四边形ADCE是菱形；
(2)解：过点D作DF⊥CE，垂足为点F，如图所示：
DF即为菱形ADCE的高，
∵∠B＝60°，CD＝BD，
∴△BCD是等边三角形，
∴∠BDC＝∠BCD＝60°，CD＝BC＝6，
∵CE∥AB，
∴∠DCE＝∠BDC＝60°，
又∵CD＝BC＝6，
∴在Rt△CDF中，DF＝3eq \r(3)．
证明：(1)∵四边形ABCD是矩形，
∴∠B＝∠C＝∠ADC＝90°，AB＝DC＝7，BC＝AD＝12，
∴∠BAF＋∠AFB＝90°，
∵DF平分∠ADC，
∴∠ADF＝∠CDF＝45°，
∴△DCF是等腰直角三角形，
∴FC＝DC＝7，
∴AB＝FC，
∵AF⊥EF，
∴∠AFE＝90°，
∴∠AFB＋∠EFC＝90°，
∴∠BAF＝∠EFC，
在△ABF和△FCE中，
∠BAF＝∠EFC；AB＝FC；∠B＝∠C，
∴△ABF≌△FCE(ASA)，
∴EF＝AF；
(2)解：BF＝BC﹣FC＝12﹣7＝5，
在Rt△ABF中，由勾股定理得：
AF＝ QUOTE 72+52 72+52＝ QUOTE 74 74，则EF＝AF＝ QUOTE 74 74.
证明：(1)∵四边形ABCD是正方形，
∴AB＝AD，∠BAE＝∠D＝90°，
又AE＝DF，
∴△ABE≌△DAF；
(2)∵△ABE≌△DAF，
∴∠FAD＝∠ABE，
又∠FAD＋∠BAO＝90°，
∴∠ABO＋∠BAO＝90°，
∴△ABO∽△EAB，
∴AB：BE＝BO：AB，即AB：6＝4：AB，
∴AB2＝24，
所以正方形ABCD面积是24．
证明：(1)∵四边形ABCD是平行四边形，
∴AB＝CD，∠BAD＝∠BCD，
由折叠的性质得：AG＝CD，∠EAG＝∠BCD，
∴AB＝AG，∠BAD＝∠EAG，
∴∠BAE＝∠GAF，
又∵AB∥CD，AE∥GF，AD∥BC，
∴∠BEA＝∠EAF＝∠GFA，
在△ABE和△AGF中，
∠BEA＝∠GFA，∠BAE＝∠GAF，AB＝AG，
∴△ABE≌△AGF(AAS)；
(2)根据折叠的性质可得AE＝EC，
设BE＝x，则AE＝EC＝8﹣x，
在直角△ABE中，根据勾股定理可得62＋x2＝(8﹣x)2，
解得：x＝eq \f(7,4)，
则S△ABE＝eq \f(1,2)AB•BE＝eq \f(1,2)×6×eq \f(7,4)＝eq \f(21,4)．
证明：(1)∵四边形ABCD是矩形，
∴AD∥BC，∠A＝90°，
∴∠MDO＝∠NBO，∠DMO＝∠BNO，
∵在△DMO和△BNO中，
，
∴△DMO≌△BNO(AAS)，
∴OM＝ON，
∵OB＝OD，
∴四边形BMDN是平行四边形，
∵MN⊥BD，
∴平行四边形BMDN是菱形.
(2)解：∵四边形BMDN是菱形，
∴MB＝MD，
设MD长为x，则MB＝DM＝x，
在Rt△AMB中，BM2＝AM2＋AB2
即x2＝(8﹣x)2＋42，解得：x＝5，
所以MD长为5.
四、综合题
解：(1)如图，过点A作AP⊥BD于点P，AF⊥BC，交CB的延长线于点F，
∵AP⊥BD，AF⊥BC，BD⊥BC
∴四边形APBF是矩形
∵∠ABC＝135°，∠DBC＝90°，
∴∠ABP＝45°，且∠APB＝90°，
∴AP＝PB，
∴四边形APBF是正方形
∴AP＝AF，且AD＝AC，
∴Rt△APD≌Rt△FAC(HL)
∴∠DAP＝∠FAC，
∵∠FAC＋∠PAC＝90°
∴∠DAP＋∠PAC＝90°
∴∠DAC＝90°
(2)如图，过点F作FM⊥BC于点M，FN⊥BD于点N，过点C作CP⊥BF于点P，在BD上截取DH＝BC，连接AH，
∵∠ABC＝135°，∠ABF＝90°，
∴∠CBF＝45°，
且∠DBC＝90°，
∴∠DBF＝∠CBF，
且FN⊥BD，FM⊥BC，
∴FN＝FM，
∵S△DBF＝2S△CBF，
∴BD＝2BC，
∴BH＝BD﹣DH＝BD﹣BC＝BC，
∵∠AED＝∠BEC，∠DAC＝∠DBC＝90°，
∴∠ADH＝∠ACB，且AD＝AC，DH＝BC，
∴△ADH≌△ACB(SAS)，
∴∠AHD＝∠ABC＝135°，AH＝AB，
∴∠AHB＝∠ABD＝45°，
∴∠HAB＝90°，
∵BC＝BH，∠HAB＝∠BPC，∠AHB＝∠FBC＝45°，
∴△AHB≌△PBC(AAS)，
∴AB＝PC，
∵AB＝PC，且∠ABP＝∠BPC，∠AGB＝∠CGP，
∴△AGB≌△CGP(AAS)，
∴AG＝GC
(3)∵AB＝3＝CP，∠PBC＝45°，CP⊥BF，
∴BP＝3，
∵△AGB≌△CGP，
∴BG＝GP＝eq \f(3,2)
在Rt△PGC中，CG＝eq \f(3,2)eq \r(5)
∴AG＝GC＝eq \f(3,2)eq \r(5)
∴AC＝AD＝3eq \r(5)
在Rt△ADC中，CD＝3eq \r(10)，
∵S△DBF＝2S△CBF，
∴DF＝2FC
∵DF＋FC＝DC
∴CF＝eq \r(10)
在Rt△PFC中，PF＝1
∴FG＝PG＋PF＝1＋eq \f(3,2)＝eq \f(5,2)
(1)证明：作EP⊥CD于P，EQ⊥BC于Q，
∵∠DCA＝∠BCA，
∴EQ＝EP，
∵∠QEF＋∠FEC＝45°，∠PED＋∠FEC＝45°，
∴∠QEF＝∠PED，
在Rt△EQF和Rt△EPD中，
，
∴Rt△EQF≌Rt△EPD(ASA)，
∴EF＝ED，
∴矩形DEFG是正方形；
(2)如图2中，在Rt△ABC中．AC＝eq \r(2)AB＝4，
∵EC＝2，
∴AE＝CE，
∴点F与C重合，此时△DCG是等腰直角三角形，易知CG＝2；
(3)①如图3，当DE与AD的夹角为40°时，
∠DEC＝45°＋40°＝85°，
∵∠DEF＝90°，
∴∠CEF＝5°，
∵∠ECF＝45°，
∴∠EFC＝130°，
②如图4，当DE与DC的夹角为40°时，
∵∠DEF＝∠DCF＝90°，
∴∠EFC＝∠DEC＝40°，
综上所述，∠EFC＝130°或40°．