2024-2025学年北京市朝阳区陈经纶中学九年级（上）期中数学试卷（含解析）

这是一份2024-2025学年北京市朝阳区陈经纶中学九年级（上）期中数学试卷（含解析），共25页。试卷主要包含了选择题，填空题等内容，欢迎下载使用。

1．（3分）抛物线的顶点坐标是
A．B．C．D．
2．（3分）用配方法解方程，变形后结果正确的是
A．B．C．D．
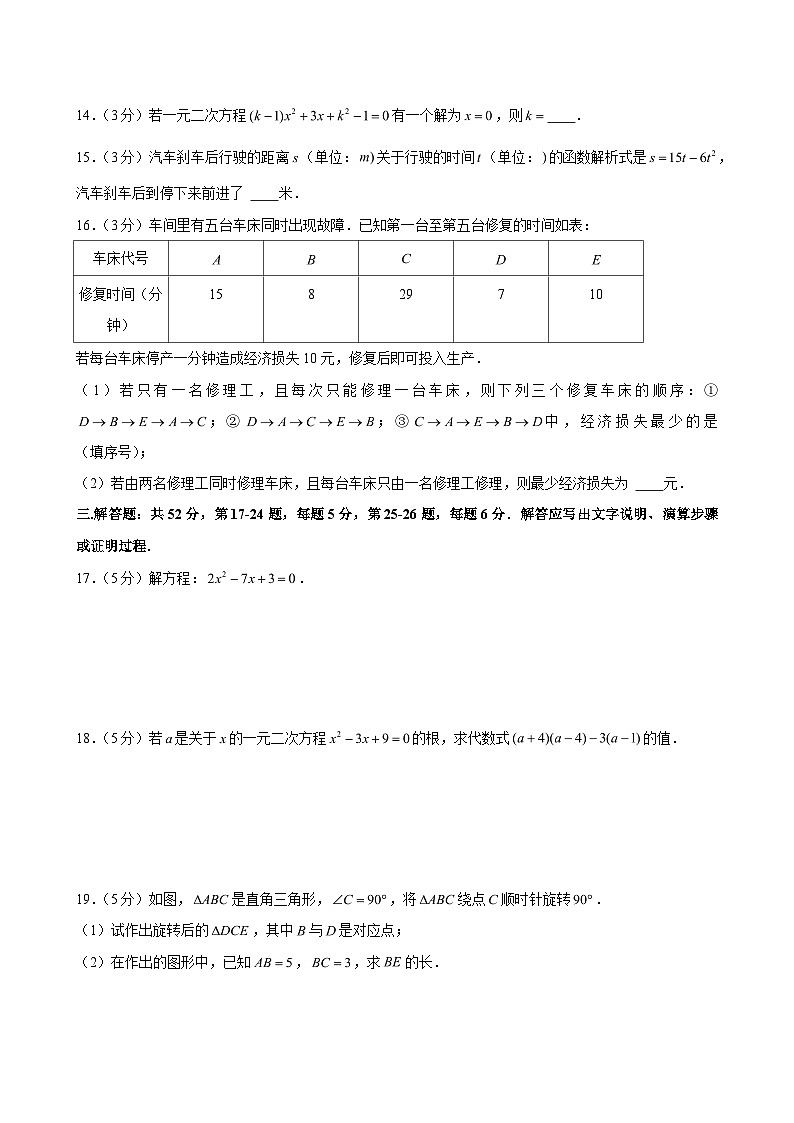
3．（3分）图中的五角星图案，绕着它的中心旋转后，能与自身重合，则的值至少是
A．B．C．D．
4．（3分）若关于的一元二次方程有两个相等的实数根，则实数的值为
A．4B．C．D．2
5．（3分）将抛物线的图象向左平移2个单位，再向下平移3个单位，得到的抛物线是
A．B．C．D．
6．（3分）如图，在平面直角坐标系中，顶点的横、纵坐标都是整数．若将以某点为旋转中心，顺时针旋转得到，其中、、分别和、、对应，则旋转中心的坐标是
A．B．C．D．
7．（3分），，，三点都在二次函数的图象上，则，，的大小关系为
A．B．C．D．
8．（3分）四位同学在研究二次函数时，甲同学发现函数图象的对称轴是直线；乙同学发现当时，；丙同学发现函数的最小值为；丁同学发现是一元二次方程的一个根，已知这四位同学中只有一位同学发现的结论是错误的，则该同学是
A．甲B．乙C．丙D．丁
二、填空题：共8个小题，每小题3分，共24分．
9．（3分）方程的根是 ．
10．（3分）请写出一个开口向上，并且与轴交于点的抛物线的表达式是 ．
11．（3分）如图，将绕点逆时针旋转，得到，若，则的度数 ．
12．（3分）如图，已知二次函数与一次函数的图象相交于点，，则的解是 ．
13．（3分）杭州亚运会的吉祥物“琮琮”“宸宸”“莲莲”组合名为“江南忆”，出自唐朝诗人白居易的名句“江南忆，最忆是杭州”，它融合了杭州的历史人文、自然生态和创新基因．吉祥物一开售，就深受大家的喜爱．经统计，某商店吉祥物“江南忆”6月份的销售量为1200件，8月份的销售量为1452件，设吉祥物“江南忆”6月份到8月份销售量的月平均增长率为，则可列方程为 ．
14．（3分）若一元二次方程有一个解为，则 ．
15．（3分）汽车刹车后行驶的距离（单位：关于行驶的时间（单位：的函数解析式是，汽车刹车后到停下来前进了 米．
16．（3分）车间里有五台车床同时出现故障．已知第一台至第五台修复的时间如表：
若每台车床停产一分钟造成经济损失10元，修复后即可投入生产．
（1）若只有一名修理工，且每次只能修理一台车床，则下列三个修复车床的顺序：①；②；③中，经济损失最少的是 （填序号）；
（2）若由两名修理工同时修理车床，且每台车床只由一名修理工修理，则最少经济损失为 元．
三.解答题：共52分，第17-24题，每题5分，第25-26题，每题6分．解答应写出文字说明、演算步骤或证明过程．
17．（5分）解方程：．
18．（5分）若是关于的一元二次方程的根，求代数式的值．
19．（5分）如图，是直角三角形，，将绕点顺时针旋转．
（1）试作出旋转后的，其中与是对应点；
（2）在作出的图形中，已知，，求的长．
20．（5分）已知抛物线图象上部分点的横坐标与纵坐标的对应值如下表：
（1）并画出图象；
（2）求此抛物线的解析式；
（3）结合图象，直接写出当时的取值范围．
21．（5分）已知关于的一元二次方程是．
（1）求证：无论取何值，方程总有两个实数根；
（2）若方程的一个实数根是另一个实数根的两倍，求的值．
22．（5分）景区内有一块米的矩形郁金香园地（数据如图所示，单位：米），现在其中修建一条花道（阴影所示），供游人赏花．若改造后观花道的面积为12平方米，求的值．
23．（5分）数学活动课上，老师提出一个探究问题：制作一个体积为，底面为正方形的长方体包装盒（如图，当底面边长为多少时，需要的材料最省（底面边长不超过，且不考虑接缝）．某小组经讨论得出：材料最省，就是尽可能使得长方体的表面积最小．下面是他们的探究过程，请补充完整：
（1）设长方体包装盒的底面边长为 ，表面积为 ．可以用含的代数式表示长方体的高为，根据长方体的表面积公式：长方体表面积底面积侧面积．得到与的关系式： ；
（2）列出与的几组对应值：（说明：表格中相关数值精确到十分位）
（3）在图2的平面直角坐标系中，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；
（4）结合画出的函数图象，解决问题：长方体包装盒的底面边长约为 时，需要的材料最省．
24．（5分）在平面直角坐标系中，抛物线的对称轴为直线，点，，，在抛物线上．
（1）当时，直接写出与的大小关系；
（2）若对于，都有，求的取值范围．
25．（6分）在中，，，将线段绕点逆时针旋转得到线段，连接，．
（1）如图1，当时，则 （用含有的式子表示）；
（2）如图2，当时，作的角平分线交的延长线于点．交于点，连接．
①依题意在图2中补全图形，并求的度数；
②用等式表示线段，，之间的数量关系，并证明．
26．（6分）对于平面直角坐标系xOy内的点P和图形M，给出如下定义：如果点P绕原点O顺时针旋转90°得到点P′，点P′落在图形M上或图形M围成的区域内，那么称点P是图形M关于原点O的“伴随点”．已知点A（1，1），B（3，1），C（3，2）．
（1）在点P1（﹣2，0），P2（﹣1，1），P3（﹣1，2）中，点 是线段AB关于原点O的“伴随点”；
（2）如果点D（m，2）是△ABC关于原点O的“伴随点”，直接写出m的取值范围；
（3）已知抛物线y＝﹣（x﹣1）2+n上存在△ABC关于原点O的“伴随点”，求n的最大值和最小值．
参考答案
一、选择题：共8个小题，每小题3分，共24分．
1．（3分）抛物线的顶点坐标是
A．B．C．D．
解：的顶点坐标为．
故选：．
2．（3分）用配方法解方程，变形后结果正确的是
A．B．C．D．
解：
．
故选：．
3．（3分）图中的五角星图案，绕着它的中心旋转后，能与自身重合，则的值至少是
A．B．C．D．
解：该图形被平分成五部分，旋转72度的整数倍，就可以与自身重合，
旋转的度数至少为，
故选：．
4．（3分）若关于的一元二次方程有两个相等的实数根，则实数的值为
A．4B．C．D．2
解：关于的一元二次方程有两个相等的实数根，
△，
解得．
故选：．
5．（3分）将抛物线的图象向左平移2个单位，再向下平移3个单位，得到的抛物线是
A．B．C．D．
解：抛物线的顶点坐标为，
向左平移2个单位，再向下平移3个单位，
平移后的抛物线的顶点坐标为，
得到的抛物线是．
故选：．
6．（3分）如图，在平面直角坐标系中，顶点的横、纵坐标都是整数．若将以某点为旋转中心，顺时针旋转得到，其中、、分别和、、对应，则旋转中心的坐标是
A．B．C．D．
解：如图，点即为所求，．
故选：．
7．（3分），，，三点都在二次函数的图象上，则，，的大小关系为
A．B．C．D．
解：二次函数的图象开口向下，对称轴为，点，，在对称轴的左侧，由随的增大而增大，有，
由，，离对称轴的远近可得，，，因此有，
故选：．
8．（3分）四位同学在研究二次函数时，甲同学发现函数图象的对称轴是直线；乙同学发现当时，；丙同学发现函数的最小值为；丁同学发现是一元二次方程的一个根，已知这四位同学中只有一位同学发现的结论是错误的，则该同学是
A．甲B．乙C．丙D．丁
解：当甲同学的结论正确，
即当函数的对称轴是直线时，，
即；
当乙同学的结论正确，
即当时，时，，
可得；
当丙同学的结论正确，
即当函数的最小值为时，，
可得；
当丁同学的结论正确，
即当时，一元二次方程的一个根时，，
可得；
根据和不能同时成立，可知乙同学和丁同学中有一位的结论是错误的，
假设丁同学的结论错误，联立和，
得，，不满足，
故假设不成立；
假设乙同学的结论错误，联立和，
得，，此时满足，
故假设成立；
故选：．
二、填空题：本大题共8个小题，每小题3分，共24分．
9．（3分）方程的根是 0或6 ．
解：
即，得或．
10．（3分）请写出一个开口向上，并且与轴交于点的抛物线的表达式是 （答案不唯一） ．
解：抛物线的解析式为．
故答案为：（答案不唯一）．
11．（3分）如图，将绕点逆时针旋转，得到，若，则的度数 ．
解：，
，
将绕点逆时针旋转，得到，
，，
，
，
故答案为：．
12．（3分）如图，已知二次函数与一次函数的图象相交于点，，则的解是 或8 ．
解：二次函数与一次函数的图象相交于点，，
方程的解是或8，
故答案为：或8．
13．（3分）杭州亚运会的吉祥物“琮琮”“宸宸”“莲莲”组合名为“江南忆”，出自唐朝诗人白居易的名句“江南忆，最忆是杭州”，它融合了杭州的历史人文、自然生态和创新基因．吉祥物一开售，就深受大家的喜爱．经统计，某商店吉祥物“江南忆”6月份的销售量为1200件，8月份的销售量为1452件，设吉祥物“江南忆”6月份到8月份销售量的月平均增长率为，则可列方程为 ．
解：根据题意得：．
故答案为：．
14．（3分）若一元二次方程有一个解为，则 ．
解：一元二次方程的一个解为0，
且，
解得．
故答案为：．
15．（3分）汽车刹车后行驶的距离（单位：关于行驶的时间（单位：的函数解析式是，汽车刹车后到停下来前进了 米．
解：，
汽车刹车后到停下来前进了米．
故答案为：．
16．（3分）车间里有五台车床同时出现故障．已知第一台至第五台修复的时间如表：
若每台车床停产一分钟造成经济损失10元，修复后即可投入生产．
（1）若只有一名修理工，且每次只能修理一台车床，则下列三个修复车床的顺序：①；②；③中，经济损失最少的是 ① （填序号）；
（2）若由两名修理工同时修理车床，且每台车床只由一名修理工修理，则最少经济损失为 元．
解：（1）要经济损失最少，就要使总停产的时间尽量短，然先修复时间短的，即按7、8、10、15、29分钟顺序修复，
故选：①；
（2）一名修理工修8分钟和15分钟，共需23分钟，一名修理工修7分钟和10分钟和29分钟共需46钟，五台机器停产的总时间为：
（分钟），
（元
故答案为：1010．
三.解答题：共52分，第17-24题，每题5分，第25-26题，每题6分．解答应写出文字说明、演算步骤或证明过程．
17．（5分）解方程：．
解：原方程可变形为
或，．
18．（5分）若是关于的一元二次方程的根，求代数式的值．
解：将代入得，
，
．
19．（5分）如图，是直角三角形，，将绕点顺时针旋转．
（1）试作出旋转后的，其中与是对应点；
（2）在作出的图形中，已知，，求的长．
解：（1）如图所示；
（2），，，
．
由旋转而成，
，
．
20．（5分）已知抛物线图象上部分点的横坐标与纵坐标的对应值如下表：
（1）并画出图象；
（2）求此抛物线的解析式；
（3）结合图象，直接写出当时的取值范围．
解：（1）根据列表画出抛物线图象如下，
（2）设二次函数的解析式为，
由题意得：当时，，
，
时，，当时，，
，
解得，
抛物线的解析式为；
（3），
当时，
当时，，当时，，
由图象可得，当时，．
21．（5分）已知关于的一元二次方程是．
（1）求证：无论取何值，方程总有两个实数根；
（2）若方程的一个实数根是另一个实数根的两倍，求的值．
【解答】（1）证明：△
，
无论取何值，此方程总有两个实数根；
（2）解：设方程有两个实数根，，
，，且
，，
，
或．
22．（5分）景区内有一块米的矩形郁金香园地（数据如图所示，单位：米），现在其中修建一条花道（阴影所示），供游人赏花．若改造后观花道的面积为12平方米，求的值．
解：根据题意，得，
整理，得，
解得：，，
园地的宽为5米，而，
不合题意，舍去．
答：的值为1．
23．（5分）数学活动课上，老师提出一个探究问题：制作一个体积为，底面为正方形的长方体包装盒（如图，当底面边长为多少时，需要的材料最省（底面边长不超过，且不考虑接缝）．某小组经讨论得出：材料最省，就是尽可能使得长方体的表面积最小．下面是他们的探究过程，请补充完整：
（1）设长方体包装盒的底面边长为 ，表面积为 ．可以用含的代数式表示长方体的高为，根据长方体的表面积公式：长方体表面积底面积侧面积．得到与的关系式： ；
（2）列出与的几组对应值：（说明：表格中相关数值精确到十分位）
（3）在图2的平面直角坐标系中，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；
（4）结合画出的函数图象，解决问题：长方体包装盒的底面边长约为 时，需要的材料最省．
解：（1）由题意，；
故答案为：；
（2）当时，；
故答案为：28.0；
（3）函数图象如图所示：
（4）观察图象可知，当约为时，需要的材料最省．
故答案为：2.2．
24．（5分）在平面直角坐标系中，抛物线的对称轴为直线，点，，，在抛物线上．
（1）当时，直接写出与的大小关系；
（2）若对于，都有，求的取值范围．
解：（1）由题意，当时，对称轴为直线．
又抛物线，
抛物线开口向上．
抛物线上的点离对称轴越近函数值越小．
又此时，，
．
点离对称轴的距离大于点离对称轴的距离．
．
（2）由题意，对于，都有，
又抛物线上的点离对称轴越近函数值越小，
，到对称轴的距离大于点到对称轴的距离，小于点到对称轴的距离，
．
①当时，
．
若，
．
又，
且．
．
若，
．
．
又，
且．
且．
此时无解．
②当时，
．
若，
．
．
又，
．
．
若，
．
．
又，
且．
且．
此时无解．
综上，或．
25．（6分）在中，，，将线段绕点逆时针旋转得到线段，连接，．
（1）如图1，当时，则 （用含有的式子表示）；
（2）如图2，当时，作的角平分线交的延长线于点．交于点，连接．
①依题意在图2中补全图形，并求的度数；
②用等式表示线段，，之间的数量关系，并证明．
解：（1）将线段绕点逆时针旋转得到线段，
，，
，
，
，
，
故答案为：；
（2）①如图所示：
，，
，，
；
②，理由如下：
如图2，过点作于，
，平分，
，，
，
，
，
，
，，
，
，
，
，
，
又，，
，
，
，
．
26．（6分）对于平面直角坐标系xOy内的点P和图形M，给出如下定义：如果点P绕原点O顺时针旋转90°得到点P′，点P′落在图形M上或图形M围成的区域内，那么称点P是图形M关于原点O的“伴随点”．已知点A（1，1），B（3，1），C（3，2）．
（1）在点P1（﹣2，0），P2（﹣1，1），P3（﹣1，2）中，点 P2和P3 是线段AB关于原点O的“伴随点”；
（2）如果点D（m，2）是△ABC关于原点O的“伴随点”，直接写出m的取值范围；
（3）已知抛物线y＝﹣（x﹣1）2+n上存在△ABC关于原点O的“伴随点”，求n的最大值和最小值．
解：（1）∵A（1，1），B（3，1），
∴AB∥x轴，
如图1，点P1（﹣2，0），P2（﹣1，1），P3（﹣1，2）绕点O顺时针旋转90°得到的对应点分别为：P1′（0，2），P2′（1，1），P3′（2，1），
其中点P2′（1，1），P3′（2，1），在线段AB上，
∴P2和P3是线段AB关于原点O的“伴随点”，
故答案为：P2和P3；
（2）当时，点D（m，2）是△ABC关于原点O的“伴随点”；理由如下：
∵A（1，1），B（3，1），C（3，2），
∴△ABC在第一象限，
∵点D（m，2）是△ABC关于原点O的“伴随点”；
∴点D在第二象限，
过点D作DP⊥x轴于点P，过点D′作D′Q⊥x轴于点Q，
则：∠DPO＝∠D′QO＝90°，
∵OD绕点O顺时针旋转90°得到OD′，
∴OD＝OD′，∠DOD′＝90°，
∴∠DOP＝∠OD′Q＝90°﹣∠D′OQ，
在△DPO和△OQD′中，
，
∴△DPO≌△OQD′（AAS），
∴OQ＝DP，D′Q＝OP，
∵D（m，2），
∴OQ＝DP＝|m|，D′Q＝OP＝2，
∵△ABC在第一象限，
∴D′（2，﹣m），
设直线AC的解析式为：y＝kx+b，则：
，
解得：，
∴，
当D′在AC上时，，
解得：；
当D′在AB上时，﹣m＝1，
解得：m＝﹣1；
∴当时，点D（m，2）是△ABC关于原点O的“伴随点”；
（3）如图3：△ABC绕点O逆时针旋转90°得到△A′B′C′，其中A′（﹣1，1），B′（﹣1，3），C′（﹣2，3）．
∵抛物线上存在△ABC关于原点O的“伴随点”，
∴当y＝﹣（x﹣1）2+n过A′，即1＝﹣（﹣1﹣1）2+n，
解得：n＝5，
∴n的最小值为5；
同理，当y＝﹣（x﹣1）2+n过C′，得到n的最大值为12．
车床代号
修复时间（分钟）
15
8
29
7
10
0
1
2
3
5
0
0
0.5
1
1.5
2
2.5
3
80.5
42.0
31.2

28.5
31.3
车床代号
修复时间（分钟）
15
8
29
7
10
0
1
2
3
5
0
0
0.5
1
1.5
2
2.5
3
80.5
42.0
31.2

28.5
31.3