河南省信阳市固始县2023-2024学年八年级下学期期末数学试卷(解析版)

这是一份河南省信阳市固始县2023-2024学年八年级下学期期末数学试卷(解析版)，共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题
1. 下列二次根式中，最简二次根式是（ ）
A. B. C. D.
【答案】B
【解析】A.，则此项不是最简二次根式，不符合题意；
B.是最简二次根式，符合题意；
C.，则此项不是最简二次根式，不符合题意；
D.，则此项不是最简二次根式，不符合题意；
故选：B．
2. 下列计算正确的是（ ）
A. B.
C. D.
【答案】D
【解析】A.与不是同类二次根式，不可合并，则此项错误，不符合题意；
B.，则此项错误，不符合题意；
C.，则此项错误，不符合题意；
D.，则此项正确，符合题意；
故选：D．
3. 在中，的对边分别为a，b，c，下列条件中，不能判定是直角 三角形的是（ ）
A. B. ，，
C. D.
【答案】C
【解析】A.，则最大角为,即是直角三角形，不符合题意；
B.由，符合勾股定理的逆定理，即是直角三角形，不符合题意；
C.，不符合勾股定理的逆定理，不是直角三角形，符合题意；
D.由，则,即是直角三角形，不符合题意．
故选：C．
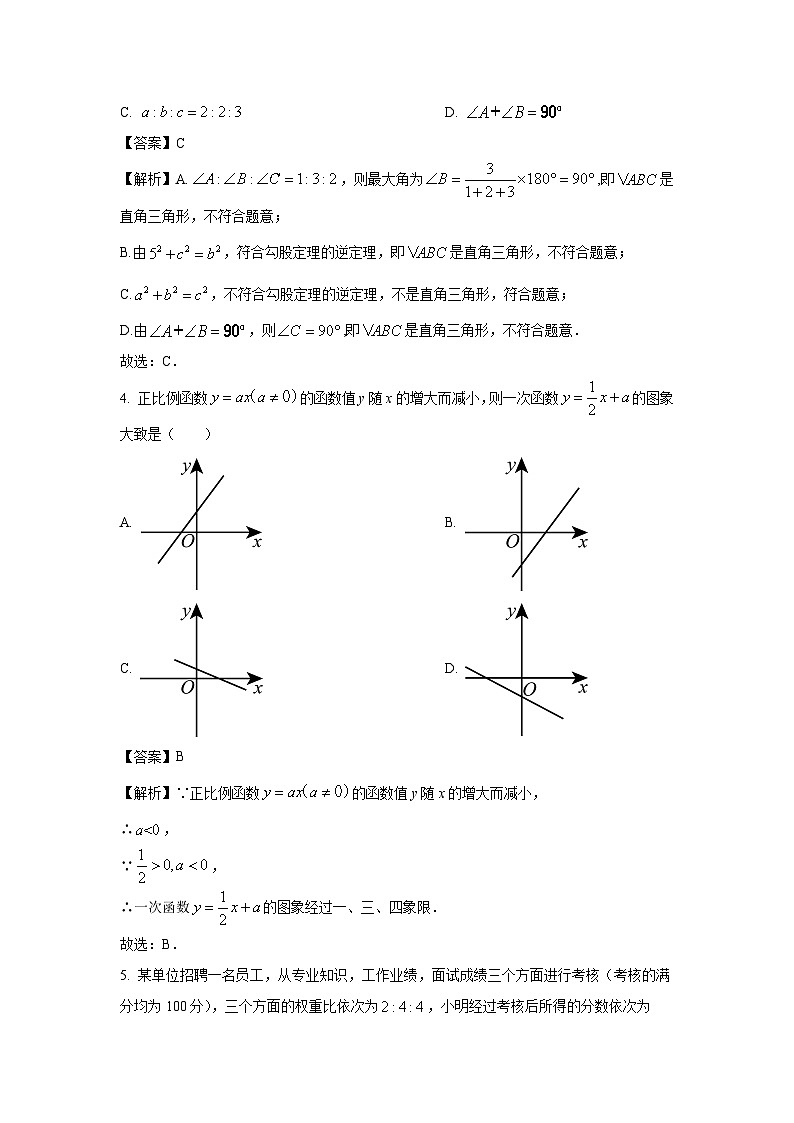
4. 正比例函数的函数值y随x的增大而减小，则一次函数的图象大致是（ ）
A. B.
C. D.
【答案】B
【解析】∵正比例函数的函数值y随x的增大而减小，
∴，
∵，
∴一次函数的图象经过一、三、四象限．
故选：B．
5. 某单位招聘一名员工，从专业知识，工作业绩，面试成绩三个方面进行考核（考核的满分均为100分），三个方面的权重比依次为，小明经过考核后所得的分数依次为90，85，80分，那么小明考核的最后得分是（ ）
A. 0B. 84C. 87D. 90
【答案】B
【解析】小明的最后得分（分），
故选：B．
6. 如图，在四边形ABCD中，已知，添加下列一个条件后，仍不能判定四边形ABCD为平行四边形的是（ ）

A. B.
C. D.
【答案】D
【解析】A.∵，
∴，
∵，
∴，
∴，
∴四边形是平行四边形，故选项A不符合题意；
B.∵，
∴，
∵，
∴四边形是平行四边形，故选项B不符合题意；
C.∵，
∴，
∵，
∴
∴四边形是平行四边形，故选项C不符合题意；
D.∵，
∴，
∵，
∴四边形可以是等腰梯形，故选项D符合题意；
故选：D．
7. 在平面直角坐标系中，若将一次函数的图象向下平移2个单位长度后经过点，则的值为（ ）
A. 5B. C. 1D.
【答案】D
【解析】将一次函数的图象向下平移2个单位长度，
平移后的直线的解析式为：，
∵过点，
∴，
解得：，
故选：D．
8. 已知一次函数 ，那么下列结论正确的是（ ）
A. y 的值随 x 的值增大而增大B. 图象经过第一、二、三象限
C. 图象必经过点D. 当 时，y<0
【答案】C
【解析】A.由于一次函数y=-x+2的k=-1<0，所以y的值随x的值增大而减小，故该选项不符合题意；
B.一次函数y=-x+2的k=-1<0，b=2>0，所以该函数过一、二、四象限，故该选项不符合题意；
C.将（0,2）代入y=-x+2中得2=0+2，等式成立，所以（0,2）在y=-x+2上，故该选项符合题意；
D.一次函数y=-x+2的k=-1<0，所以y的值随x的值增大而减小，所以当x<2时，y>0，故该选项不符合题意．
故选：C．
9. 如图，点P是正方形的对角线上一点，于点E，于点F，连接，给出下列5个结论：①，②，③一定是等腰三角形，④⑤，其中正确的结论个数是（ ）
A. 2个B. 3个C. 4个D. 5个
【答案】B
【解析】延长FP交AB于点N，延长AP交EF于点M．
∵四边形ABCD是正方形．
∴∠ABP=∠CBD，
又∵NP⊥AB，PE⊥BC，
∴∠PNB=∠NBE=∠PEB=90°，PN=PE，
∴四边形BNPE是正方形，∠ANP=∠EPF，
∴NP=EP，
∴AN=PF，
在△ANP与△FPE中，
，
∴△ANP≌△FPE（SAS），
∴AP=EF，∠PFE=∠BAP（故①④正确）；
△APN与△FPM中，∠APN=∠FPM，∠NAP=∠PFM，
∴∠PMF=∠ANP=90°，
∴AP⊥EF，（故②正确）；
P是BD上任意一点，因而△APD是等腰三角形和PD=2EC不一定成立，（故③⑤错误）；
故正确的是：①②④．
故选：B．
10. 如图，是平面直角坐标系中轴上的一点，，以为底构造等腰，且，将沿着射线方向平移，每次平移的距离都等于线段的长，则第2024次平移结束时，点的对应点的坐标为（ ）
A. B.
C. D.
【答案】D
【解析】如图，作于点C，
，，，，
，，
，
，
由图观察可知，第1次平移相当于点向上平移1个单位，向右平移个单位，第2次平移相当于点向上2平移个单位，向右平移个单位，……
以此类推，第n次平移后点的对应点坐标为，
第2024次平移结束时，点的对应点的坐标为，即，
故选D．
二、填空题
11. 若代数式有意义，则实数x的取值范围为______．
【答案】且
【解析】由题意得，，
∴且，
故答案为：且．
12. 请写出一个图象经过的函数的解析式____________．
【答案】(答案不唯一)
【解析】经过点的函数的解析式可以为，
故答案为：（答案不唯一）．
13. 甲、乙、丙、丁四人进行射击测试，每人10次射击成绩的平均数均是环，方差分别为，，，，则成绩最稳定的是___．
【答案】丁
【解析】因为，，，，
所以，由此可得成绩最稳定的为丁．
故答案为：丁．
14. 如图，，，分别是各边的中点，是高，如果，那么的长为___．
【答案】
【解析】∵、分别是的中点，
∴为的中位线，
∵，
∴，
∵，且F为的中点，
∴．
故答案为：．
15. 如图，一次函数分别与坐标轴交于，，点M为y轴上一点，把直线沿翻折，点B刚好落在x轴上，则点M的坐标为______．

【答案】或
【解析】如图所示，当点在轴正半轴上时，

设沿直线将折叠，点正好落在轴上的点，则有，
∵，，
，，
，
，
点的坐标为．
设点坐标为，则，，
，
，
，
；
如图所示，当点在轴负半轴上时，

，
设点坐标为，则，，
，
，
，
，
故答案为：或．
三、解答题
16. 计算：
（1）；
（2）．
解：（1）
（2）
17. 教育部在落实“双减”的同时，推动“双增”，即增加学生参加户外活动、体育锻炼、艺术活动、劳动活动的时间和机会，增加学生接受体育和美育教育的时间和机会，确保学生的身心健康．甲、乙两名队员参加射击选拔赛，射击成绩见统计图：

根据以上信息，整理分析数据如下：
（1）直接写出表格中a，b，c的值；
（2）求出d的值；
（3）若从甲、乙两名队员中选派其中一名队员参赛，你认为应选哪名队员？请结合表中的四个统计量，作出简要分析．
解：（1）乙的平均数（环）
甲射击的成绩从小到大排列为：3、6、7、8、8、9、9、9、10、10
甲射击成绩的中位数（环）
甲射击成绩中出现次数最多的是9
故，，；
（2）方差
（3）
应选甲，理由如下：
因为甲的平均数，中位数，众数均高于乙，所以应选甲．
18. 如图，王师傅在铁片中剪切下，且，，．

（1）求的长；
（2）若，，求图中阴影部分的面积．
（1）解：在中，
根据勾股定理可得，
即的长为；
（2）解：在中，
，，，
，
，
，
即图中阴影部分的面积为．
19. 若直线，，则称直线为这两条直线的友好直线．
（1）直线与的友好直线为________．
（2）已知直线是直线与的友好直线，且直线经过第一、三、四象限，与轴相交于点．
①求的取值范围；
②若直线经过定点，且，求值．
解：（1）直线y=3x+2与y=-4x+3的友好直线为：y=（3-4）x+2×3=-x+6
故答案为：y=-x+6；
（2）①直线与的友好直线为，
根据题意，得，解得．
②由①得，由，得，
当时，，
直线一定过定点．
与y轴的交点A(0，-6m)
当时，可得，即，
解得．
，则
20. 某校计划租用甲、乙两种客车送330名师生去研学基地开展综合实践活动．已知租用一辆甲型客车和一辆乙型客车共需600元，租用2辆甲型客车和3辆乙型客车共需1560元．甲客车每辆可坐30名师生，乙型客车每辆可坐45名师生．
（1）租用甲、乙两种客车每辆各需多少元？
（2）若学校计划租用8辆客车，怎样租车可使总费用最少？
解：（1）设租用甲种客车每辆元，租用乙种客车每辆元，
根据题意可得，，
解得．
答：租用甲种客车每辆240元，租用乙种客车每辆360元；
（2）设租用甲型客车辆，则租用乙型客车辆，租车总费用为元，
则，解得，
根据题意可知，，
又∵，
∴随的增大而减小，
∴当时，的最小值为．
答：当租用甲型客车2辆，租用乙型客车6辆，租车总费用最少为2640元．
21. 如图，已知平行四边形ABCD．
（1）若M，N是BD上两点，且BM＝DN，AC＝2OM，求证：四边形AMCN是矩形；
（2）若∠BAD＝120°，CD＝3，AB⊥AC，求平行四边形ABCD的面积．
（1）证明：∵四边形ABCD是平行四边形，
∴OA＝OC，OB＝OD，
∵对角线BD上的两点M、N满足BM＝DN，
∴OB﹣BM＝OD﹣DN，即OM＝ON，
∴四边形AMCN是平行四边形，
∵AC＝2OM，
∴MN＝AC，
∴四边形AMCN是矩形；
（2）解：∵四边形ABCD是平行四边形，
∴AD∥BC，AB＝CD＝3，
∴∠BAD+∠ABC＝180°，
∵∠BAD＝120°，
∴∠ABC＝60°，
∵AB⊥AC，
∴∠BAC＝90°，
∴∠BCA=30°
∴BC=6
∴AC＝3，
∴平行四边形ABCD的面积＝AC•AB＝33＝9．
22. 2月11日左右，河北省教育厅公布《河北省初中学业水平体育与健康科目考试方案》（下称《方案》）．方案提到，河北中考体育总分50分，跑步为必考项目．甲、乙两名同学相约在同一路段进行跑步训练，二人在起点会合后，甲出发3分钟时，乙出发，结果乙比甲提前2分钟到达终点．二人到达终点即停止，全程匀速．如图，设甲离开起点后经过的时间为x（分），甲离开起点的路程y（米）与x（分）之间的函数关系式为，图像为线段；乙离开起点的路程（米）与x（分）之间的函数关系用线段表示，请根据图像中的信息解决下列问题：

（1）图像中m的值为_______，n的值为_______；
（2）求线段BC对应的函数表达式（不必写出自变量的取值范围）；
（3）直接写出点D的坐标，并解释点D坐标表示的实际意义．
解：（1）当时，，
解得：，
则，
故答案为：20；18．
（2）由（1）得：，
由甲出发3分钟时，乙出发可知，设线段对应的函数表达式为，将，代入得：，
解得，
∴线段对应的函数表达式为．
（3）由题意得：，
解得：，
∴，
∴点D坐标表示的实际意义是甲出发12分钟后，乙在距出发点1800米的地方追上甲．
23. 综合与实践
问题背景：
我们知道，三角形的中位线平行于三角形的第三边，并且等于第三边的一半，如何证明三角形中位线定理呢？

已知：如图1，在中，D、E分别是的中点，求证：，．
思路分析：问题中既要证明两条线段所在的直线平行，又要证明其中一条线段的长等于另一条线段长的一半，我们可以用“倍长法”将延长一倍：即延长到F，使得，连接，通过证明四边形与四边形是平行四边形从而得出最后结论．
问题解决：
（1）上述材料中“倍长法”体现的数学思想主要是______．（填入选项前的字母代号即可）
A．数形结合思想 B．转化思想 C．分类讨论思想 D．方程思想
（2）请根据以上思路分析，完成“三角形中位线定理”的证明过程．
方法迁移：
（3）如图3，四边形和均为正方形，连接，N是的中点，连接，已知线段．请求出线段的长．
（1）解：述材料中“倍长法”体现的数学思想主要是转化思想，
故选B．
（2）证明：延长到F，使得，连接，
∵E是的中点，
∴
∵
∴四边形为平行四边形，
∴，，
∵D是的中点，
∴
∴，，
∴四边形为平行四边形，
∴，，
∵
∴，
（3）解：延长到M，使得，连接，

∵N是的中点，
∴
∴
∴四边形是平行四边形
∴，，
∴，
∵四边形和都是正方形，
∴
∴，
∴
∴
∴．
队员
平均数（环）
中位数（环）
众数（环）
方差（环）
甲
7.9
b
c
4.09
乙
a
7
7
d